alquimiayciencias: Matrices Gamma de Dirac (30521)

Si buscamos información por la red acerca de la ecuación de Dirac seguramente que lo que encontremos se parezca a esto:

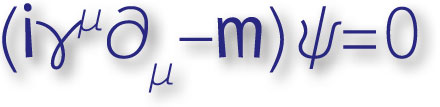
En la versión que estamos viendo aparecen las famosas matrices gamma de Dirac $\gamma^\mu$ . El objetivo de esta entrada es la de presentar estas matrices y las propiedades operacionales que tienen.

También nos entretendremos en jugar con ellas ya que son esenciales a la hora de hacer cálculos en teoría cuántica de campos cuando estamos trabajando con fermiones.

He de confesar que trabajar con las matrices de Dirac siempre me ha inspirado sentimientos contrapuestos, desde el aburrimiento más absoluto hasta cierta perversión por ver si podía deducir todas las expresiones que vamos a presentar en esta entrada (y muchas más).

En siguientes entradas iremos a desgranar su significado físico y matemático a un nivel más conceptual. Pasen y vean.

De alfa y beta a gamma

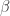Como hemos visto las $\alpha_i$ y la $\beta$ son matrices que tienen que cumplir ciertas propiedades:

1.- Son matrices linealmente independientes.

2.- Sin traza.

3.- Hermíticas.

4.- Su cuadrado nos da la identidad.

5.- Anticonmutan entre ellas.

6.- El rango mínimo admisible es de 4.

Ahora lo que vamos a hacer es una trivialidad, vamos a cambiar de nombre a algunas matrices.

$\beta=\gamma^0$

$\beta\alpha_i=\gamma^i$

Con esto tenemos cuatro matrices: $\{\gamma^0,\gamma^1,\gamma^2,\gamma^3\}$ .

Escribamos la ecuación de Dirac en términos de las gammas:

1.- Partimos de la ecuación:

$i\partial_0\psi=\left(\alpha_1(-i\partial_1)+\alpha_2(-i\partial_2)+\alpha_3(-i\partial_3)\right)\psi+\beta m\psi$

2.- De forma compacta es: $i\partial_t\psi=\left[-i\alpha_i\partial_i)+\beta m\right]\psi$

3.- Multiplicamos por 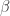$\beta$ por la izquierda:

$i\beta\partial_o\psi=\left[-i\beta\alpha_i\partial_i+\beta\beta m\right]\psi$

4.- Recordando que $\beta\beta=\mathbb{I}$ , y que $\beta=\gamma^0$ , $\beta\alpha_i=\gamma^i$ , tenemos:

$i\gamma^0\partial_o\psi=\left[-i\gamma^i\partial_i)+m\right]\psi$

5.- Agrupando, y llamando $\gamma^\mu$ donde $\mu=0,1,2,3$ :

$i\gamma^\mu\partial_\mu\psi-m\psi=0$

Jugando con las gamma y sus índices

A simple vista las matrices $\gamma^\mu$ conforman un vector en un espacio de Minkowski. En realidad, la cosa es un poco más complicada, y entraremos en detalles próximamente.

Ahora supondremos que son, efectivamente, un vector en Minkowski que es lo que da a entender su índice.

Así, dado $\gamma^\nu$ podemos bajar su índice multiplicándola por la métrica de Minkowski $\eta_{\mu\nu}$ .

En todo este curso supondremos que la métrica es de signatura -2, eso quiere decir que su diagonal es $\eta_{\mu\nu}=diag(+1,-1,-1,-1)$ .

$\eta_{\mu\nu}=\begin{pmatrix}+1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1\end{pmatrix}$

Dada una métrica de Minkowski $\eta_{\mu\nu}$ tenemos una inversa $\eta^{\mu\nu}$ de forma que:

$\eta_{\mu\nu}\eta^{\nu\sigma}=\begin{pmatrix}+1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1\end{pmatrix}\begin{pmatrix}+1&0&0&0\\ 0&-1&0&0\\ 0&0&-1&0\\ 0&0&0&-1\end{pmatrix}=$

$=\begin{pmatrix}+1&0&0&0\\ 0&+1&0&0\\ 0&0&+1&0\\ 0&0&0&+1\end{pmatrix}=\delta^\sigma_\mu$

La métrica nos sirve para subir y bajar índices:

$\gamma_\nu=\eta_{\mu\nu}\gamma^\nu$

Es evidente que si $\gamma^\mu=\{\gamma^0,\gamma^1,\gamma^2,\gamma^3\}$ , el resultado de bajar el índice es: $\gamma_\mu=\{\gamma_0,-\gamma_1,-\gamma_2,-\gamma_3\}$

Además definiremos la matriz $\gamma^5$ que se define como:

$\gamma^5=i\gamma^0\gamma^1\gamma^2\gamma^3$

Esta matriz será muy importante para nosotros y es muy, pero que muy bueno acostumbrarse a ella y a sus propiedades.

Lo que vamos a hacer en lo que sigue es lo siguiente:

Vamos a comprobar las relaciones de anticonmutación entre las gammas.
Calcularemos sus cuadrados.
Vamos a calcular distintas trazas de distintos productos de gammas.
También vamos a estudiar si estas matrices son hermíticas o no.

Relaciones de Anticonmutación y Cuadrados

1.- Calcularemos los cuadrados $\left(\gamma^0\right)^2=+1\times\mathbb{I}_{4\times 4}$ y $\left(\gamma^i\right)^2=-1\times\mathbb{I}_{4\times 4}$

Comprobación:

Emplearemos las definiciones $\gamma^0=\beta$ y $\gamma^i=\beta\alpha_i$ .

Con lo cual $\gamma^0\gamma^0=\beta\beta=\mathbb{I}=+1\times\mathbb{I}$ .

Y para $\gamma^i\gamma^i=\beta\alpha_i\beta\alpha_i$ . Como sabemos:

$\beta\beta=\mathbb{I}$ (de ahora en adelante omitiremos el factor 4×4 ya que no estudiaremos otro caso hasta que digamos lo contrario).

$\alpha_i\alpha_i=\mathbb{I}$

$\alpha_i\beta=-\beta\alpha_i$ Entonces podemos concluir:

$\gamma^i\gamma^i=\beta\alpha_i\beta\alpha_i=-\beta\beta\alpha_i\alpha_i=-1\times\mathbb{I}$

2.- Ahora vamos a calcular el anticonmutador de dos matrices gamma y obtendremos:

$\{\gamma^\mu,\gamma^\nu\}=2\eta^{\mu\nu}\times\mathbb{I}_{4\times 4}$

Comprobación:

Lo haremos por casos:

1º caso $\mu=\nu=0$

$\{\gamma^0,\gamma^0\}=\{\beta,\beta\}=\beta\beta+\beta\beta=\mathbb{I}+\mathbb{I}=2\times\mathbb{I}$

2º caso $\mu=0$ y $\nu=i$

$\{\gamma^0,\gamma^i\}=\{\beta,\beta\alpha_i\}=\beta\beta\alpha_i+\beta\alpha_i\beta=$

$=\beta\beta\alpha_i-\beta\beta\alpha_i=0$

3º caso $\mu=i\neq\nu=j$

$\{\gamma^i,\gamma^j\}=\{\beta\alpha_i,\beta\alpha_j\}=\beta\alpha_i\beta\alpha_j+\beta\alpha_j\beta\alpha_i=$

$=-\beta\beta\alpha_i\alpha_j-\beta\beta\alpha_j\alpha_i=-(\alpha_i\alpha_j+\alpha_j\alpha_i)=-\{\alpha_i,\alpha_j\}=0$

Recordemos que las matrices alfa anticonmutan entre ellas.

4º caso $\mu=\nu=i$ aprovechando los resultados de 1.-) tendremos:

$\{\gamma^i,\gamma_i\}=2\gamma^i\gamma^i=-2\times\mathbb{I}$

Así pues recolectando todos los casos vemos como el anticonmutador de dos gamma cero nos da 2 x (1) x I y el de dos gamma-i nos da 2 x (-1) x I.

El resto de combinaciones son nulas.

Estas son las componentes de la diagonal de la métrica de Minkowski con lo que se puede escribir:

$\{\gamma^\mu,\gamma^\nu\}=2\eta^{\mu\nu}\times\mathbb{I}_{4\times 4}$

Volveremos a este interesante punto de la relación entre el anticonmutador de las matrices gamma de Dirac y la métrica del espaciotiempo.

3.- Vamos a comprobar que $(\gamma^5)^2=\mathbb{I}$ :

Comprobación:

Usando la definición tendremos:

$(i\gamma^0\gamma^1\gamma^2\gamma^3)(i\gamma^0\gamma^1\gamma^2\gamma^3)=-\gamma^0\gamma^1\gamma^2\gamma^3\gamma^0\gamma^1\gamma^2\gamma^3=$

Como matrices gamma diferentes anticonmutan cada vez que cambiemos de orden dos matrices gamma introduciremos un cambio de signo:

$=\gamma^0\gamma^1\gamma^2\gamma^0\gamma^3\gamma^1\gamma^2\gamma^3=-\gamma^0\gamma^1\gamma^0\gamma^2\gamma^3\gamma^1\gamma^2\gamma^3=$

$=\gamma^0\gamma^0\gamma^1\gamma^2\gamma^3\gamma^1\gamma^2\gamma^3=\gamma^1\gamma^2\gamma^3\gamma^1\gamma^2\gamma^3=$

$=-\gamma^1\gamma^2\gamma^1\gamma^3\gamma^2\gamma^3=\gamma^1\gamma^1\gamma^2\gamma^3\gamma^2\gamma^3=$

Recordemos que $\gamma^i\gamma^i=-1\times\mathbb{I}$ :

$=-\gamma^2\gamma^3\gamma^2\gamma^3=\gamma^2\gamma^2\gamma^3\gamma^3=(-\mathbb{I})(-\mathbb{I})=\mathbb{I}$

4.- Probaremos que $\{\gamma^5,\gamma^\mu\}=0$

Comprobación:

Lo haremos en dos casos concretos y el resto se haría análogamente.

1º caso

$\{\gamma^5,\gamma^0\}=\{i\gamma^0\gamma^1\gamma^2\gamma^3,\gamma^0\}=i\{\gamma^0\gamma^1\gamma^2\gamma^3,\gamma^0\}=i(\gamma^0\gamma^1\gamma^2\gamma^3\gamma^0+\gamma^0\gamma^0\gamma^1\gamma^2\gamma^3)=$

Efectuamos cambios en la posición de gamma-cero de la primera expresión y en la otra empleamos que su cuadrado nos da la identidad:

$=i(-\gamma^0\gamma^1\gamma^2\gamma^0\gamma^3+\gamma^1\gamma^2\gamma^3)=i(\gamma^0\gamma^1\gamma^0\gamma^2\gamma^3+\gamma^1\gamma^2\gamma^3)=i(-\gamma^0\gamma^0\gamma^1\gamma^2\gamma^3+\gamma^1\gamma^2\gamma^3)=$

$=i(-\gamma^1\gamma^2\gamma^3+\gamma^1\gamma^2\gamma^3)=0$

2º caso

Usaremos la gamma-5 y la gamma-2, con cualquier otra sirve el argumento:

$\{\gamma^5,\gamma^2\}=i\{\gamma^0\gamma^1\gamma^2\gamma^3,\gamma^2\}=i(\gamma^0\gamma^1\gamma^2\gamma^3\gamma^2+\gamma^2\gamma^0\gamma^1\gamma^2\gamma^3)=$

$=i(-\gamma^0\gamma^1\gamma^2\gamma^2\gamma^3-\gamma^0\gamma^2\gamma^1\gamma^2\gamma^3)=i(\gamma^0\gamma^1\gamma^3+\gamma^0\gamma^1\gamma^2\gamma^2\gamma^3)=$