miércoles, 26 de octubre de 2016

Café Matemático... La fórmula de Bailey-Borwein-Pluff

Esta notable identidad asegura que
\displaystyle{\pi = \sum_{k=0}^\infty \frac{1}{16^k} \left ( \frac{4}{8k+1}-\frac{2}{8k+4} - \frac{1}{8k+5} - \frac{1}{8k+6}\right ).}
La fórmula BBP se utiliza para calcular cualquier dígito hexadecimal de 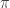\pi sin necesidad de calcular los dígitos anteriores, reduciendo la complejidad del cálculo.
La demostración de esta identidad es bastante sencilla porque sólo utiliza conocimientos básicos de cálculo infinitesimal. Tenemos por una parte
\displaystyle{\int_0^{1/\sqrt{2}} \frac{x^{k-1}}{1-x^8}\,dx =\int_0^{1/\sqrt{2}} \sum_{j=1}^\infty x^{8j+k-1}\,dx = \frac{1}{2^{k/2}}\sum_{j=0}^\infty \frac{1}{16^j (8j+k)},}
de modo que
\displaystyle{\sum_{k=0}^\infty \frac{1}{16^k} \left ( \frac{4}{8k+1}-\frac{2}{8k+4} - \frac{1}{8k+5} - \frac{1}{8k+6}\right )=\int_0^{1/\sqrt{2}}\frac{4 \sqrt{2}-8x^3+4 \sqrt{2}x^4-8x^5}{1-x^8}\,dx.}
Aplicando el cambio de variable 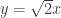y = \sqrt{2}x\, y el algoritmo de descomposición en fracciones simples esta integral se convierte en
\displaystyle{\int_0^1 \frac{16y-16}{y^4-2y^3+4y-4}\,dy=\int_0^1 \frac{4y}{y^2-1}\,dy-\int_0^1 \frac{4y-8}{y^2-2y+2}\,dy=\pi.}
Publicado por en

No hay comentarios:

Publicar un comentario