Teorema: 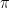 es irracional
es irracional
Demostración
Definimos la siguiente función:
Utilizando el binomio de Newton podemos expresar 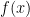 así:
así:
>
Cuando  se tiene que
se tiene que 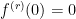 (al derivar menos de
(al derivar menos de  veces el término
veces el término  no desaparece del todo) y cuando
no desaparece del todo) y cuando 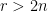 también obtenemos que
también obtenemos que 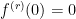 (ya que la propia función es la función
(ya que la propia función es la función 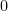 al derivar más veces que su propio grado). Para calcular el resto de las derivadas en
al derivar más veces que su propio grado). Para calcular el resto de las derivadas en 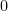 tomamos
tomamos 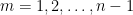 y las calculamos para todo
y las calculamos para todo  :
:
Teniendo en cuenta esta expresión vemos fácilmente que 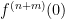 es un número entero para
es un número entero para 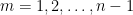 .
.
Por tanto tenemos que 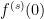 es un número entero
es un número entero  . Como
. Como  también tenemos que
también tenemos que 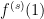 es un número entero
es un número entero  .
.
Después de estos preliminares vamos con la demostración. En realidad vamos a demostrar que  es irracional, hecho del que se deduce muy fácilmente que
es irracional, hecho del que se deduce muy fácilmente que 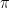 es irracional (¿Por qué?). La demostración comienza suponiendo que
es irracional (¿Por qué?). La demostración comienza suponiendo que  es racional, es decir,
es racional, es decir, 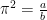 , con
, con 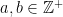 , es decir, enteros positivos. Definimos para cualquier entero positivo
, es decir, enteros positivos. Definimos para cualquier entero positivo  la siguiente función:
la siguiente función:
Al ser 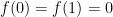 y
y 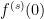 un número entero
un número entero 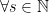 se tiene que
se tiene que 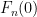 y
y 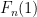 son enteros (los denominadores que aparecerían al sustituir
son enteros (los denominadores que aparecerían al sustituir  por su supuesta expresión como fracción se cancelarían con el término
por su supuesta expresión como fracción se cancelarían con el término  del principio).
del principio).
Realizamos ahora el siguiente cálculo basado en la función 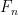 :
:
Sustituyendo  por
por  tenemos:
tenemos:
Integrando obtenemos lo siguiente (pasamos 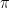 dividiendo a la derecha):
dividiendo a la derecha):
que, como hemos visto antes, es un número entero.
Por otro lado, es sencillo demostrar que para  se tiene que
se tiene que 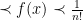 . Multiplicando a ambos lados por
. Multiplicando a ambos lados por 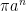 obtenemos:
obtenemos:
Multiplicamos por 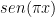 y acotamos la parte de la derecha (ya que
y acotamos la parte de la derecha (ya que 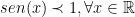 ):
):
Integrando entre 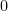 y
y 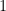 obtenemos:
obtenemos:
Pero la última fracción es menor que 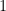 para
para  suficientemente grande. Por tanto tenemos lo siguiente:
suficientemente grande. Por tanto tenemos lo siguiente:
Pero habíamos visto antes que 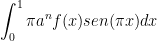 era un número entero. Es decir, hemos llegado a un número entero entre
era un número entero. Es decir, hemos llegado a un número entero entre 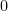 y
y 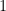 . Esa es la contradicción.
. Esa es la contradicción.
Por tanto  es irracional y en consecuencia
es irracional y en consecuencia 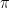 también lo es.
también lo es.
No hay comentarios:
Publicar un comentario
Este blog es un espacio para hablar de ciencias y sentires, compartir aquello que quieras preguntar y vivenciar curiosidades....