
La conjetura de Hilbert–Pólya (Montgomery, 1973) es un camino para demostrar la hipótesis de Riemann. Basta hallar un hamiltoniano (operador autoadjunto no acotado) cuyos autovalores sean los ceros de la función. El físico Carl M. Bender y varios colegas han encontrado un hamiltoniano PT simétrico con esta propiedad (una variante no hermítica del operador de Berry–Keating). No siendo hermítico no permite una demostración. ¿Será el punto de partida para una demostración de la conjetura de Hilbert–Pólya? La mayoría de los expertos tienen muchas dudas al respecto.
La solución de los grandes problemas de las matemáticas siempre viene acompañada de una comprensión más profunda del campo de las matemáticas en las que se sitúa el problema. El nuevo hamiltoniano PT simétrico está construido ad hoc y no ofrece ninguna información profunda sobre los problemas de teoría de números que la hipótesis de Riemann debe iluminar. Se puede afirmar sin rubor que se trata de una tautología. Y, por tanto, nadie espera que suponga ningún avance hacia la resolución del problema abierto más importante de la matemática contemporánea.
Siendo darle malas noticias a quienes hayan leído a Natalie Wolchover, “Physicists Attack Math’s $1,000,000 Question,” Quanta Magazine, 04 Apr 2017. Admiro el trabajo de Bender, padre de los sistemas PT simétricos, pero no puedo opinar otra cosa sobre su artículo Carl M. Bender, Dorje C. Brody, Markus P. Müller, “Hamiltonian for the Zeros of the Riemann Zeta Function,” Phys. Rev. Lett. 118: 130201 (30 Mar 2017), doi: 10.1103/PhysRevLett.118.130201, arXiv:1608.03679 [quant-ph]. Lo leí con interés y atención hace ya un año, pero no me pareció relevante reseñarlo en este blog. También recomiendo el reciente Jens Bolte, Sebastian Egger, Stefan Keppeler, “The Berry-Keating operator on a lattice,” J. Phys. A 50: 105201 (2017), doi: 10.1088/1751-8121/aa5844, arXiv:1610.06472 [math-ph].
En la línea de mi crítica recomiendo leer a Peter Woit, “Some Math and Physics Interactions,” Not Even Wrong, 05 Apr 2017. Por cierto, Carl Bender tenía un blog, hoy abandonado; recomiendo leer “PT-Quantum Mechanics,” Eikonal Blog, 18 Apr 2011.
[PS 07 Abr 2017] Para los matemáticos, recomiendo la discusión del artículo en “Riemann hypothesis: is Bender-Brody-Müller Hamiltonian a new line of attack?” Mathematics, Stack Exchange, 31 Mar 2017. En concreto, Jean V. Bellissard analiza las dificultades analíticas del nuevo hamiltoniano y concluye que “as long as physicists use algebra, or algorithmic arguments, they can find outstanding results. But when it comes to analysis, they may loose their judgment, and grave mistakes show up at the corner. Analysis is not easily amenable to algoritmic descriptions. And this is precisely where the power of Mathematics lies.” [/PS]

La hipótesis de Riemann afirma que los ceros no triviales de la función zeta de Riemann tienen parte real exactamente igual a un medio. Hay ingentes indicios numéricos de este hecho y su demostración rigurosa está dotada con un millón de dólares (Problema del Milenio del Instituto Clay). La conjetura de Hilbert–Pólya afirma que la existencia de un operador hermítico cuyos autovalores reales correspondan a los ceros de la función zeta es suficiente para demostrar la hipótesis de Riemannn.
El trabajo de Berry y Keaton ha llevado a la conjetura de que el hamiltoniano clásico asociado a dicho hamiltoniano cuántico debe tener la forma H = x p. Encontrar un hamiltoniano hermítico con esta propiedad raya lo imposible.
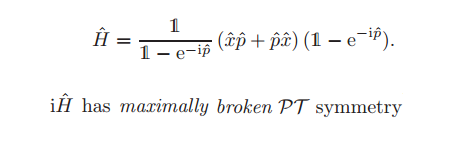
La propuesta de Bender y sus colegas es un hamiltoniano PT invariante cuyo límite clásico es H = 2 x p. No siendo hermítico no permite usar directamente la conjetura de Hilbert–Pólya. Más aún, no parece fácil construir un operador hermítico inspirado en este nuevo hamiltoniano. No soy experto, pero las palabras optimistas de Bender y sus colegas en su artículo en Physical Review Letters parecen escritas con la tinta del diablo.
Han permitido la aceptación del artículo, pero a un matemático que intente demostrar la hipótesis de Riemann no le sirven absolutamente para nada. Una pena.
Como siempre, espero que mi opinión esté equivocada.
No hay comentarios:
Publicar un comentario