A veces, la inmensa mayoría de las veces, volver a estudiar hechos y conceptos que damos por supuesto y/o aprendidos es un ejercicio muy útil que nos proporciona una visión diferente y bastante enriquecedora.
Más aún si se trata de conceptos relativos a la Mecánica Cuántica que, seamos sinceros, no hay nadie absolutamente nadie que la entienda, y el que diga que lo hace miente como un bellaco.
Vamos a ver un ejemplo de esto en esta entrada.
Imaginemos que nos tiramos de cabeza contra un muro.
Lo más probable es que nos rompamos la crisma y que se nos quiten las ganas de hacerlo de nuevo.

Ahora bien, supongamos que nos transformamos en una partícula y que nuestra dinámica está regida por la leyes de la Mecánica Cuántica.
La situación cambia completamente (nota para los expertos: hay alguna licencia en esta parte en aras de una mayor claridad en la analogía).
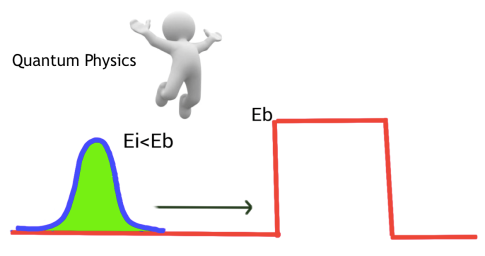
Por un lado tendríamos una función de onda, asociada dada por la dualidad onda-corpúsculo, y una probabilidad distinta de cero de atravesar la barrera sin partirnos la cabeza.
Esto es lo que se conoce como efecto túnel.
Este efecto es muy conocido, y de hecho tiene muchísimas aplicaciones hoy en día como por ejemplo el Microscopio de Efecto Túnel (Scanning Tunnelling Microscope STM).
Sin embargo, no por conocido este fenómeno deja de ocultar sorpresas. Si pudiéramos tomar una imagen del momento en el que la función de onda, es decir la partícula, está atravesando la barrera “veríamos” que parte de la función de onda está por fuera de la barrera y parte de la función de onda está dentro de la barrera.
De hecho como la energía se tiene que conservar (atención a las cursivas) nunca toda la función puede estar totalmente debajo de la barrera. Siempre tiene que existir parte por fuera de ésta.
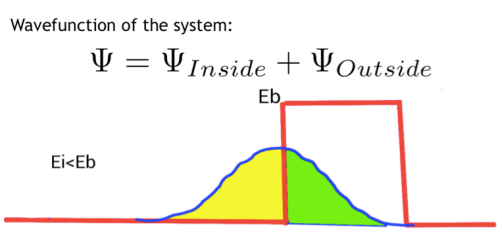
Si en esta situación midiéramos la energía de la función de onda completa obtendríamos la energía inicial Ei.

Hasta aquí todo claro.
¿Pero qué pasaría si pudiéramos medir exclusivamente la energía de la parte de la función de onda que está debajo de la barrera?
Tras darle un par de vueltas tendríamos que concluir , o al menos eso creo yo, que la energía es Eb.
Es decir mediaríamos una energía mucho mayor que la energía inicial Ei con los evidentes problemas que eso implica.

En este punto muchos y con razón podemos decir que por un lado no existe un experimento posible, o al menos a mí no se me ocurre, para medir exclusivamente la parte de la función de onda que está por debajo de la barrera en el efecto túnel, y por otro que si ese experimento existiera la propia medida, ¡ay el problema de la medida!, interaccionaría con el sistema y que las cosas no serían tan sencillas como las estoy planteando.
Tienen toda la razón, pero hay una forma de medir un proceso análogo. Un proceso que podemos inducir mediante la interacción láser-materia…
Como vamos a entrar en un terreno un tanto complicado vayamos paso a paso.
Por un lado sabemos que los estados accesibles de un átomo o molécula, un sistema de ahora en adelante, están cuantizados.
Es decir un sistema solo absorberá un fotón si la energía de éste coincide con la diferencia de energía entre el estado fundamental, el estado de menor energía, y un estado excitado.
En el caso del átomo de hidrógeno estas diferencias son:13.6-3.40 eV, 13.6-1.51 eV, y así sucesivamente.

Sin embargo esto no es siempre así, y las cosas no son siempre tan sencillas. Supongamos un sistema en su estado de menor energía con su estado fundamental y su primer estado excitado, y un láser pulsado con frecuencia central ω tal que la energía de sus fotones (hω) difiere por una cantidad Δ (detuning) de la diferencia de energía entre los estados considerados.
Este detuning se elige mayor que la incertidumbre en energía (por la relación de incertidumbre energía-tiempo) del pulso láser.
De forma técnica el detuning debe ser mayor que el bandwidth del láser.

En estas condiciones y aunque como decíamos antes los fotones del láser tengan una energía menor que el gap de energía entre los estados, la Mecánica Cuántica nos dice que durante la interacción láser-materia existe una probabilidad no nula de encontrar el sistema en el estado excitado (!).
En términos técnicos decimos que existe una transferencia de población desde el estado fundamental al estado excitado.
Al cesar la interacción la población retorna al estado fundamental y el sistema queda como si nada hubiera pasado.
Debido a este retorno este proceso se conoce como Coherent Population Return (CPR) existiendo muchas referencias bibliográficas (entre ellas mi tesis) sobre las posibles aplicaciones experimentales.

Si nos fijamos bien, mediante CPR hemos conseguido una situación similar a la que describíamos al principio de este post.
La función de onda que describe nuestro sistema tiene una componente asociada al estado fundamental que es análoga a la parte que está fuera de la barrera en los ejemplos de tunnelling.
También tiene una componente asociada a un fenómeno que “en principio no es posible” que es la componente asociada al estado excitado que resulta análoga a la parte de la función de onda que está debajo de la barrera.
Sin embargo existe una diferencia fundamental ya que en el caso de CPR sí podemos medir la parte de la función de onda correspondiente al proceso “no permitido”.
Basta con utilizar un segundo láser que ionize la población transferida al estado excitado y detectar los iones generados.

Ajustando la energía de los fotones del láser de ionización, que no afecta para nada al láser de CPR, podemos conseguir una situación en la que ionicemos un sistema pero siendo la suma de las energías de los fotones absorbidos menor que el potencial de ionización (!!!).
Las cosas se están empezando a complicar un poco.
Tenemos un fenómeno que se puede describir de forma muy fácil teóricamente, de hecho es un ejercicio muy interesante para cualquier estudiante de Mecánica Cuántica, que se puede demostrar experimentalmente, pero que sin embargo no admite una interpretación sencilla ya que todo apunta a que la energía no se conserva.

El asunto es desde luego espinoso y hay que andarse con pies de plomo para no patinar.
De hecho tras unos 4 años trabajando en esto aún no tengo claro como solucionar esta “paradoja”. Al menos sí tengo claro algunas cosas:
1.- No es un efecto del bandwidth
Los láseres pulsados por tener una duración temporal finita tienen asociados un bandwidth, es decir una incertidumbre en frecuencia (o de forma equivalente una incertidumbre en energía), que para pulsos gaussianos cumple la ecuación:
Se podría pensar que teniendo en cuenta las incertidumbres en energía de los láseres de CPR y de ionización se podría salvar la conservación de la energía. Sin embargo es fácil demostrar que la ionización se produce independientemente del detuning Δ que elijamos para el láser de CPR. De hecho la condición para que CPR funciones es que el detuning sea mayor que el bandwidth del láser.
También es posible demostrar experimentalmente y analíticamente que la señal de iones que se obtiene es incompatible con que sea un efecto del bandwidth.
2.- ¿Conservación de la energía en un proceso que depende del tiempo?
Se puede argumentar y con razón que hablar de la conservación de la energía durante un proceso dependiente del tiempo es algo cuando menos dudoso.
De hecho si el hamiltoniano que describe el proceso que estamos estudiando depende del tiempo, la ecuación en Mecánica Cuántica que describe la evolución del valor medio de los operadores nos dice que la energía no se conserva.

Sin embargo si hacemos el balance de energía olvidándonos del momento de la interacción podemos fácilmente comprobar como la energía final es mayor que la inicial.

3.- En interacción láser-materia la materia se trata de forma cuántica y la radiación de forma clásica resultando un tratamiento semiclásico.
Efectivamente. A la hora de resolver la Ecuación de Schrödinger dependiente del tiempo, la materia se trata de forma cuántica, con estado cuantizados, y la radiación de forma clásica.
De hecho un pulso láser se describe por una función envolvente, típicamente una gaussiana, multiplicada por una función oscilante (seno o coseno) que da información sobre la frecuencia de la radiación.
Sin embargo hay varias razones que me hacen pensar que el tratamiento no es el problema.
Por un lado muchos efectos puramente cuánticos, como por ejemplo Electromagnetic Induced Transparency (EIT), son extremadamente bien descritos por un tratamiento semiclásico de la interacción. Y por otro, es posible avanzar hacia un tratamiento “más cuántico” aunque aún semiclásico si se describe el pulso láser en función de los operadores escalera. Es decir si se aplica el modelo de Jaynes-Cummings.
Si se toman el tiempo para describir la interacción usando este formalismo podréis comprobar con sorpresa como el resultado es exactamente el que predice la teoría semiclásica (yo lo he hecho).
Como es habitual en Física sabemos qué no es la respuesta a nuestro problema pero seguimos sin saber cual es la respuesta en sí.
Veamos ahora algunas posibilidades que yo calificaría como plausibles. Más adelante veremos las “ideas locas” fruto de la desesperación.
1.- El concepto de fotón
Si lo pensamos detenidamente el fotón surge de la cuantización de un campo eléctrico ideal. Un campo eléctrico que no depende del tiempo y que por supuesto no está interaccionando con nada.
Sin embargo en este ejemplo estamos usando este concepto de fotón en una situación dependiente del tiempo y de interacción.
¿Tiene sentido hablar de fotones en este caso?
Dicho de otra forma, ¿sabemos contar el número de fotones que se absorben para el caso de CPR?
Porque claro está, si los fotones no tuvieran que absorberse de forma entera, si por ejemplo el sistema pudiera absorber ¾ de un fotón, tendríamos el problema solucionado. ¿Estamos “forzando” demasiado este concepto con nuestras ecuaciones y nuestra interpretación de éstas?
Le he dado muchas vueltas a este asunto con muchos colegas muy inteligentes y la única conclusión a la que hemos llegado es que no estamos seguros.
Hoy por hoy no puedo dar una respuesta clara a esto. ¿Alguna idea?
2.- El concepto de tiempo en Mecánica Cuántica.
Aquí hay que andarse con pies de plomo porque es sencillo patinar.
El tiempo en Mecánica Cuántica es cuando menos peculiar.
Es una variable que se introduce “a presión” en las ecuaciones que describen la interacción y que a veces nos juega malas pasadas.
De hecho la dependencia temporal de la interacción láser-materia es la responsable de que todas las descripciones matemáticas que hagamos sean semiclásicas. Una descripción puramente cuántica produciría un Hamiltoniano no dependiente del tiempo, el pulso láser se describiría como una superposición de modos de fotones, y por tanto tendríamos que la energía se conserva sin problemas.
Para esto necesitaríamos de una Teoría Cuántica de Campos que dependa del espacio y del tiempo que sea capaz de describir una situación de interacción.
Hoy por hoy yo no conozco a nadie capaz de hacer esto, de una forma u otra el tiempo siempre acaba apareciendo de forma artificial y “jodiendo” el invento.
De hecho si lo pensamos detenidamente las implicaciones de la variable tiempo en Mecánica Cuántica son muchas y variadas.
Por ejemplo la relación de incertidumbre energía-tiempo no es “natural” como puede ser la relación “posición-momento” porque el tiempo no tiene operador asociado.
El formalismo está “como forzado” para acoger esta relación de incertidumbre.
Como podéis ver el asunto no está nada pero nada claro, y tras interminables discusiones siempre surgen ideas locas….
1.- La energía no se conserva.
Quizás el concepto de energía en Mecánica Cuántica es mucho más complejo de lo que pensamos. Especialmente si tenemos situaciones de interacción dependiente del tiempo. Al fin y al cabo la conservación de la energía es un principio y no una ley. Vale que se cumple en el 99.9999% de los casos, pero en nuestra desesperación he de confesar que lo hemos llegado a valorar.
2.- ¿Y el vacío?
Hasta ahora no hemos considerado la interacción con el vacío.
Es decir no hemos tenido en cuenta esos estados del vacío que pueden acoplarse con los estados propios de los átomos o moléculas.
El asunto no es baladí ya que incluso para una correcta descripción de un fenómeno tan básico como es la emisión espontánea hay que considerar estos estados o modos del vacío.
¿Es necesario para CPR considerar el vacío y así salvar la conservación de la energía?
¿Estamos drenando energía del vacío?
Si han llegado hasta aquí, espero que sí, con la intención de encontrar una solución de esta aparente paradoja siento decepcionaros.
No sé cual es la respuesta.
Tras unos años trabajando en este tema solo hemos conseguido enredarnos cada vez más. Al abrir un puerta nos encontramos con dos más.
En el fondo supongo que he comprobado en mis carnes la famosa frase de Richard Feynmann que decía:
“Si usted piensa que entiende a la mecánica cuántica… entonces usted no entiende la mecánica cuántica”
