Ecuación de difusión convectiva
La deducción de la ecuación se realiza a partir de un balance de materia a un volumen de control infinitesimal. Para el caso de la difusión, vamos a suponer que las partículas entran al volumen de control con una cierta velocidad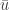 
, que determina la tasa a la que las partículas son arrastradas hacia el volumen de control.
, que determina la tasa a la que las partículas son arrastradas hacia el volumen de control.
Para el volumen de control dado, el flujo de partículas va según el eje 
, por tanto, el flujo de partículas entrantes viene dado por la siguiente relación:
, por tanto, el flujo de partículas entrantes viene dado por la siguiente relación:![\displaystyle{\delta y\delta z\left[n\cdot u_{x} -\frac{\delta x}{2}\frac{\partial\left(n\cdot u\right)}{\partial x}\right]}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cdelta+y%5Cdelta+z%5Cleft%5Bn%5Ccdot+u_%7Bx%7D+-%5Cfrac%7B%5Cdelta+x%7D%7B2%7D%5Cfrac%7B%5Cpartial%5Cleft%28n%5Ccdot+u%5Cright%29%7D%7B%5Cpartial+x%7D%5Cright%5D%7D&bg=ffffff&fg=333333&s=0 "\displaystyle{\delta y\delta z\left[n\cdot u_{x} -\frac{\delta x}{2}\frac{\partial\left(n\cdot u\right)}{\partial x}\right]}")
Para el flujo saliente tenemos análogamente:
![\displaystyle{\delta y\delta z\left[n\cdot u_{x} +\frac{\delta x}{2}\frac{\partial\left(n\cdot u\right)}{\partial x}\right]}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B%5Cdelta+y%5Cdelta+z%5Cleft%5Bn%5Ccdot+u_%7Bx%7D+%2B%5Cfrac%7B%5Cdelta+x%7D%7B2%7D%5Cfrac%7B%5Cpartial%5Cleft%28n%5Ccdot+u%5Cright%29%7D%7B%5Cpartial+x%7D%5Cright%5D%7D&bg=ffffff&fg=333333&s=0 "\displaystyle{\delta y\delta z\left[n\cdot u_{x} +\frac{\delta x}{2}\frac{\partial\left(n\cdot u\right)}{\partial x}\right]}")
Recordemos que la diferencia entre lo que entra y lo que sale es la tasa de acumulación de partículas según el eje x:
.
Para el resto de los ejes se obtienen expresiones análogas. Sumando para los tres ejes, obtenemos la tasa neta de acumulación:
![\displaystyle{-\delta x\delta y\delta z\left[\frac{\partial\left(n\cdot u\right)}{\partial x}+\frac{\partial\left(n\cdot u\right)}{\partial y}+\frac{\partial\left(n\cdot u\right)}{\partial z}\right]\, =\, -\delta x\delta y\delta z \bar{\nabla}\cdot n\cdot \bar{u}}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%7B-%5Cdelta+x%5Cdelta+y%5Cdelta+z%5Cleft%5B%5Cfrac%7B%5Cpartial%5Cleft%28n%5Ccdot+u%5Cright%29%7D%7B%5Cpartial+x%7D%2B%5Cfrac%7B%5Cpartial%5Cleft%28n%5Ccdot+u%5Cright%29%7D%7B%5Cpartial+y%7D%2B%5Cfrac%7B%5Cpartial%5Cleft%28n%5Ccdot+u%5Cright%29%7D%7B%5Cpartial+z%7D%5Cright%5D%5C%2C+%3D%5C%2C+-%5Cdelta+x%5Cdelta+y%5Cdelta+z+%5Cbar%7B%5Cnabla%7D%5Ccdot+n%5Ccdot+%5Cbar%7Bu%7D%7D&bg=ffffff&fg=333333&s=0 "\displaystyle{-\delta x\delta y\delta z\left[\frac{\partial\left(n\cdot u\right)}{\partial x}+\frac{\partial\left(n\cdot u\right)}{\partial y}+\frac{\partial\left(n\cdot u\right)}{\partial z}\right]\, =\, -\delta x\delta y\delta z \bar{\nabla}\cdot n\cdot \bar{u}}")
.
La ecuación anterior es la ecuación de difusión pura y dura, sin tener en cuenta los efectos de fuerzas externas. Teniendo en cuenta dichas fuerzas llegamos a la siguiente expresión:
Podemos reorganizar un poco la ecuación anterior, ya que vista así parece un poco más farragosa de lo que en realidad es.
Además, vamos a desarrollar el término 
.
.
Asumiento flujo incompresible (a veces también son estos flujos incomprensibles) esto es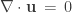 
, que el coeficiente de difusión 
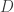es constante y dividiendo por el elemento diferencial de volumen 
llegamos a la ecuación de difusión:
, que el coeficiente de difusión es constante y dividiendo por el elemento diferencial de volumen llegamos a la ecuación de difusión:
El campo de velocidades del fluido 
viene determinado por el régimen mecánico del fluido.
viene determinado por el régimen mecánico del fluido.
En algunos casos, dicho campo de velocidades puede ser obtenido resolviendo las ecuaciones de Navier-Stokes.
Por supuesto, ya sabéis que el coeficiente de difusión puede obtenerse según varias perspectivas y campos distintos de enfoque.
