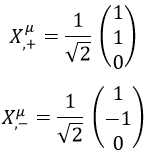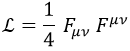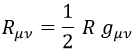
vimos que tanto el electrón como el fotón, una vez fijado su cuadrimomento, tenían dos grados de libertad o configuraciones de espín disponibles.
En el caso del fotón lo demostramos usando las ecuaciones de Maxwell y la propagación de los campos eléctrico y magnético, pero en realidad es mucho más fácil demostrar que las perturbaciones electromagnéticas solo tienen dos grados de libertad usando el cuadripotencial.
En esta entrada deduciremos los dos grados de libertad de los fotones usando coordenadas cono luz para el campo electromagnético y, de paso, usaremos los mismos conceptos para demostrar lo mismo con respecto al gravitón de Einstein.
Las coordenadas cono luz:
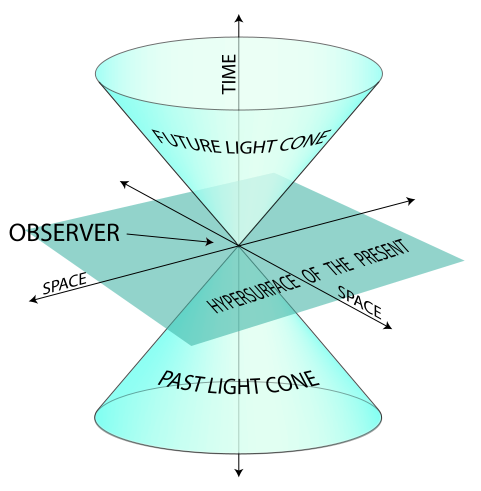
¿Y qué son las coordenadas cono luz? Pues básicamente una parametrización del espacio tiempo muy útil cuando tratamos con partículas que se mueven a la velocidad de la luz (1 en unidades naturales).
Se las denomina x+ y x- y son coordenadas obtenidas de combinar la de tiempo t y la de una dimensión concreta del espacio x (típicamente la que más nos convenga, como la que sigue una partícula):
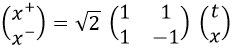
Cuando una partícula sin masa, digamos un fotón o un gravitón, se mueve en la dirección positiva del eje x a la velocidad de la luz, x- se anula.
En el caso contrario se anula x+. En cualquier otro caso no se anula ninguna de las dos componentes. Si etiquetamos como x en negrita todas las coordenadas espaciales distintas a la x elegida previamente, el espacio-tiempo se parametriza en coordenadas cono luz del siguiente modo:
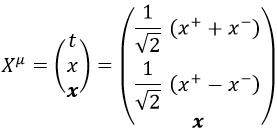
Esta expresión sería general para un número de dimensiones espaciales D arbitrario.
Las derivadas de la cuadriposición respecto a x+ y a x- serían:
Ambos cuadrivectores representan trayectorias tipo luz de módulo negativo, y multiplicados el uno por el otro escalarmente según la regla relativista dan 1:
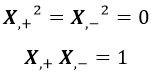
Con lo cual, la métrica relativista de Minkowski η tomaría la siguiente forma en coordenadas cono luz:

Aquí la I representaría una matriz identidad en todas las dimensiones a mayores, cuyas componentes serán etiquetadas con I.
Así pues, si queremos obtener la norma de un cuadrivector, podemos hacerlo de dos modos diferentes según las coordenadas que elijamos:
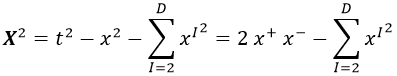
En lo que resta de entrada usaremos la segunda expresión para desarrollar productos escalares y contracciones de índices cuando proceda.
El campo electromagnético:
El campo electromagnético, como sabemos, está determinado por el cuadripotencial A y sus variaciones en el espacio-tiempo. No obstante, distintos valores de cuadripotencial pueden dar lugar a los mismos fenómenos electromagnéticos. Cuando cambiamos sus valores de forma que esto suceda decimos que estamos realizando una transformación gauge sobre el campo, que a priori es imperceptible mediante efectos secundarios.
La palabra “gauge” procede del alemán, y básicamente el concepto sería algo así como “transformación que da las mismas medidas”.
-Cinemática:
El campo electromagnético F se obtiene a partir del cuadripotencial mediante una derivada covariante antisimétrica oderivada exterior:
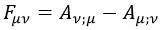
Y F es la única magnitud relevante en los experimentos, de modo que si variamos A de forma que sea irrelevante una vez que se le aplique una derivada exterior nos quedaremos como estábamos. Esto se deduce también de la lagrangiana del campo electromagnético libre, que era de la forma:
A partir de esta, se podía deducir que el momento conservado del cuadripotencial P es el propio campo F.
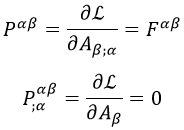
La última ecuación define dos de las ecuaciones de Maxwell en el vacío, y en función del cuadripotencial se puede escribir del siguiente modo:
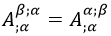
Esta es la ecuación con la que una onda electromagnética se autoimpulsa a sí misma, sin necesidad de agentes externos. Es la ecuación de un fotón.
-Transformación gauge:
Supongamos que tenemos un campo escalar ε y que transformamos el cuadripotencial del siguiente modo:
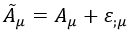
Resulta evidente que el campo electromagnético F que produce es el mismo que antes de producirse dicha transformación:

De modo que la transformación que hemos realizado es una transformación gauge, tal y como queríamos. Dado un campo electromagnético, es imposible saber el valor de ε en el cuadripotencial porque es irrelevante a priori.
Algunos experimentos parecen sugerir lo contrario, pero ya lo comentaremos en otra ocasión.
-Gauge cono luz:
La ecuación del autoimpulso electromagnético tiene, según el índice β, D+1 condiciones, siendo D el número de dimensiones espaciales. Ahora nos proponemos mostrar que algunas de ellas son irrelevantes o dependientes de las otras.
En el gauge cono luz consideraremos siempre la hipótesis de que la partícula que se mueve no lo hace hacia atrás en el eje x, de modo que x+ nunca será nulo. En caso de que dicha condición no se cumpla, podemos hacer que sí lo haga girando el sistema de coordenadas que usamos para analizar el movimiento. Una vez considerada esta hipótesis, imponemos que las componentes + de los campos gauge a considerar sean nulas.
Antes de ver cómo funciona esto, recordemos que en mecánica cuántica podemos relacionar una derivada covariante con el cuadrimomento p de una partícula mediante la relación:
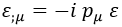
Así pues, si queremos cargarnos la componente + del cuadripotencial transformado, debe cumplirse:
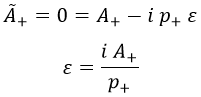
Con esto fijamos el valor exacto de ε y tenemos que llegar a las mismas conclusiones a las que llegaríamos con otro valor. De lo contrario no sería una transformación gauge. Nótese que podemos dividir entre p+ bajo la hipótesis cono luz de que la partícula no se moverá hacia atrás en el eje x. Si lo hiciese, p+ sería nulo.
-Grados de libertad:
Tomemos ahora la ecuación del autoimpulso en función del cuadrimomento:

Si fijamos que β tome el valor +, como nos hemos cargado dicha componente del cuadripotencial se tiene que cumplir una relación entre la componentente A- y las demás:
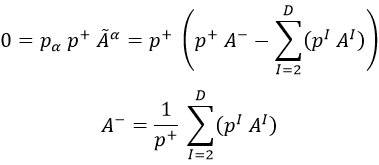
Además, de la primera ecuación se deduce que en el gauge cono luz la parte de la derecha de la ecuación de autoimpulso es nula tome el valor que tome β, con lo que queda:
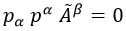
Que es exactamente la ecuación de Klein-Gordon para campos cuánticos escalares sin masa y cuya solución son ondas desplazándose por el espacio con un cuadrimomento p.
Esto implica que las distintas componentes del cuadripotencial o son nulas o oscilan como ondas. ¿Y cuántas componentes hay en D+1 dimensiones? Pues D+1. Ahora bien, una es como si fuese nula por el gauge y otra más queda fijada por su relación con el resto, en este caso A-, con lo que realmente solo hay D-1 grados de libertad:
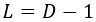
Y en 3 dimensiones espaciales, tal y como sucede en la realidad, el fotón solo posee dos espines o grandos de libertad.
Si denotamos por ξ el vector de espín de un fotón, podemos identificar un estado cuántico del campo electromagnético A mediante operadores de creación electromagnéticos a sobre el vacío sumando para todos los posibles espines la cantidad de ese espín que tienen:
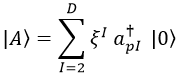
Las oscilaciones trasversales (direcciones I) generadas de este modo fijan A-, y A+ siempre diríamos que vale 0.
El campo gravitatorio:
Desde la relatividad general, denominamos campo gravitatorio a la métrica g del espacio-tiempo, que se puede ver alterada en diferentes regiones del universo.
Este campo también posee transformaciones gauge, por lo que podemos llegar a calcular los grados de libertad de sus gravitones asociados mediante el mismo protocolo que con el campo electromagnético.
-Cinemática:
El campo gravitatorio libre, igual que el electromagnético, también puede autoimpulsarse y propagarse como una onda gravitatoria o conjunto de gravitones. Su movimiento tiene una lagrangiana asociada, pero aún no ha aparecido en este blog y no procede desarrollarla ahora, así que simplemente diremos que la gravedad en el vacío cumple las ecuaciones de Einstein en ausencia de materia.
Comenzábamos definiendo la conexión afín de la métrica del siguiente modo:

Teniendo la conexión afín, era posible definir el tensor y el escalar de Ricci como:
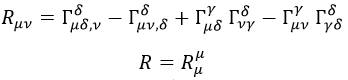
Tanto la conexión afín como el tensor de Ricci serían simétricos en los índices μ y ν.
Usando estos ingredientes, la ecuación de Einstein para el autoimpulso gravitatorio sería:
En este caso, no obstante, g en sí mismo no representaría un gravitón en movimiento, sino que es necesario definirlo a parte a diferencia de lo que sucedía con el cuadripotencial.
-El gravitón:
Un gravitón es una diminuta perturbación del espacio-tiempo. ¿Cómo de diminuta? Lo que sea necesario para que cumpla una ecuación de evolución de Klein-Gordon sin masa, como veremos que cumple.
Comenzamos descomponiendo la métrica g en la vacía de Minkowski η más una pequeña perturbación h de la misma.h*h sería demasiado grande, así que los términos en los que pueda aparecer multiplicándose a sí misma de cualquier modo serán descartados:
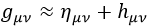
A partir de esta aproximación, la traza de h sería:
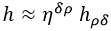
La conexión afín queda del siguiente modo si tenemos en cuenta que las derivadas de η son nulas al ser esta constante:
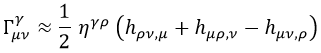
Como todas las componentes de la conexión son proporcionales a h, y hemos dicho que evitaremos multiplicarla por sí misma, el tensor de Ricci se aproxima del siguiente modo:
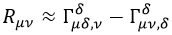
Para calcular los términos de la derecha hacemos las siguientes cuentas y adaptaciones de índices:
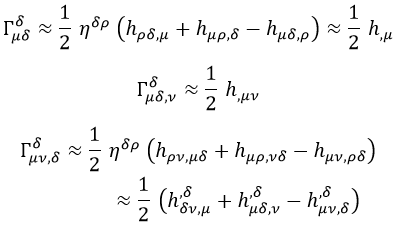
Con lo que el tensor de Ricci resultante es:
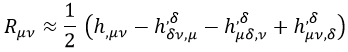
Cuya traza sería nula:
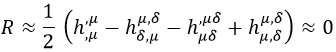
La nulidad de esta traza no es evidente, pero se saca viendo que hay tantos términos sumando como restando y que todos contribuyen las mismas veces con los mismos valores al sumar sobre μ y δ.
Siendo este el caso, la ecuación de autoimpulso gravitatoria sería:
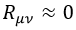
Con lo que para el “gravitón” h impondremos:
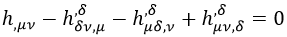
Una ecuación bastante fea, pero que de nuevo gracias a la transformación gauge y al gauge cono luz quedará mucho más sencilla.
-Transformación gauge:
Para el gravitón, la forma de transformarlo que no altera el tensor de Ricci es la siguiente:
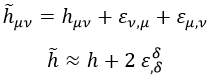
Esto, de nuevo, puede ser comprobado haciendo las cuentas a lo bruto y viendo que se cancela todo lo que se tiene que cancelar:

De modo que, en suma, a un gravitón podemos transformarlo mediante un vector espacio-temporal ε mediante la relación indicada sin peligro de que altere sus efectos. Dicho vector tendrá D+1 grados de libertad que podremos fijar a nuestro gusto para cargarnos componentes de h.
-Gauge cono luz:
Como en el caso electromagnético y por los mismos motivos, buscaremos cargarnos las componentes con + del gravitón, lo que brinda las siguientes D+1 ecuaciones que fijan las componentes de ε:
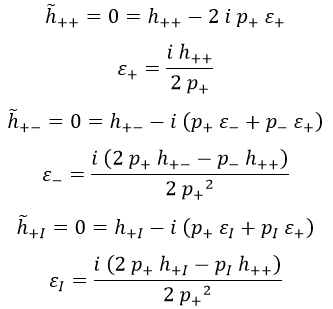
-Grados de libertad:
Antes de nada, escribamos la ecuación del autoimpulso en términos del cuadrimomento del gravitón:
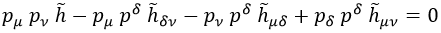
Si fijamos μ y ν para que ambas componentes sean +, obtenemos que necesariamente la traza del gravitón es nula:
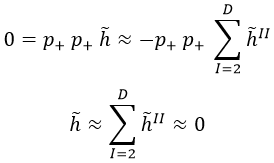
Esto deja el autoimpulso del siguiente modo:
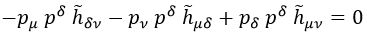
Y si ahora fijamos solo que μ sea +, obtenemos lo siguiente:
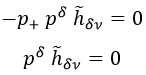
Denominaremos a esta ecuación el teorema de conservación de h, dado que si tenemos en cuenta que p es una derivada a nivel cuántico, estamos diciendo que la derivada de h es nula. Esta es una propiedad que cabía esperar dado que definimos las ecuaciones de Einstein de modo que la métrica tuviese derivada covariante nula.
Dicha expresión, cuando fijamos ν igual a – brinda una relación entre h– y las componentes h-I:
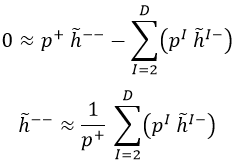
Análogamente, cuando fijamos ν igual a cualquier I brinda una relación entre la componente h-I asociada y las componentes hIJ:
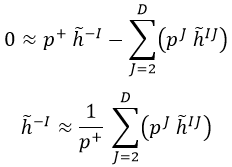
Por último, teniendo en cuenta el teorema de conservación de h, el autoimpulso finalmente toma la sencilla forma:
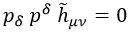
En principio h tiene (D+1)*(D+1) componentes, al ser una matriz cuadrada. Sin embargo, tenemos que tener en cuenta que todas las filas y columnas asociadas a una componente + son irrelevantes y que las asociadas a una componente –hemos visto que dependen de las trasversales. Consecuentemente, solo tendría (D-1)*(D-1) componentes independientes a nivel dinámico. Sin embargo, no todas son tal, ya que h es un tensor simétrico y además sabemos que su traza es nula.
Esto hace que los grados de libertad de un gravitón sean los de un tensor de rango 2 simétrico en un espacio de D-1 dimensiones restándoles 1:
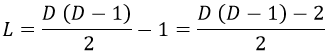
En el caso de tener 3 dimensiones espaciales, el gravitón tiene solo 2 grados de libertad, igual que el fotón, que serían la componente h22 y la h23, por ejemplo. Todas las demás dependerían de esas 2. También sería posible reducir todo a las componentes h23 y h33.
Nótese que ambas cumplirían la ecuación de Klein-Gordon sin masa en cualquier caso, que es la expresión final a la que llegamos con el autoimpulso.
No obstante, cabe destacar que el espín del gravitón y el del fotón tienen naturalezas estructurales diferentes, al ser el primero vectorial y el segundo matricial. En particular, siendo ambos bosones el primero tiene espín 1 y el segundo espín 2.
Por último, si denotamos por ξ la matriz espinorial del gravitón, podemos expresar un estado cuántico gravitatorio del siguiente modo:
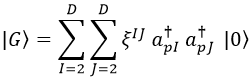
Quiero acabar esta entrada diciendo que, si bien todas las cuentas y consideraciones hechas son correctas, esta cuantización del campo gravitatorio no encaja bien en el Modelo Estándar de la física de partículas y por eso se dice que no hay una teoría cuántica de la gravedad que funcione.
En venideras entradas veremos que en una teoría de cuerdas el gravitón, no obstante, aparece con naturalidad.