Una de las conclusiones más impactantes que predice la teoría de cuerdas es que el universo tiene que tener un número de dimensiones distinto del que percibimos de forma evidente en nuestra vida diaria.
Menos conocido es, sin embargo, que para que ciertos aspectos de la teoría encajen en principio puede haber que reinterpretar qué entendemos por una suma.
Este debate en principio sigue abierto y puede suponer que simplemente toda la teoría esté mal, pero no está de más dedicar una entrada a jugar con series de números y ver a qué conclusiones chocantes y “evidentemente” absurdas llegamos.
¿Puede la suma de todos los números naturales no ser entera, ni mayor que el primero de ellos, ni positiva?
Tal vez, y solo tal vez, en algunos contextos sí.
Repaso al problema:
En la entrada anterior sobre la cuantización de las cuerdas vimos que aparecía un término d cuyo valor dependía del número de dimensiones espaciales D del espacio y de la suma de todos los números naturales:

Si la suma de todos los números naturales es infinita, d es infinito y se acabó la fiesta o el número de dimensiones es 1.
La teoría no funciona. Si no es infinita, puede pasar cualquier cosa.
Siendo este el caso, pusimos un interrogante en la suma S de todos los números naturales:
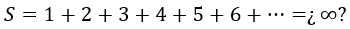
Las series divergentes pueden sumar lo que nos dé la gana:
Antes de abordar el problema, veamos un ejemplo sencillo de cómo podemos jugar con una serie divergente para que nos dé el resultado que queramos. Pongamos por caso la sucesión a1n que consta de 1 y -1 alternados:
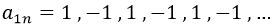
Definamos ahora S1 como la suma de todos sus términos:
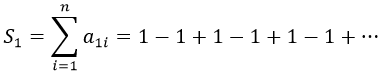
¿Las matemáticas estándar asignan algún resultado concreto a esta cuenta? No, en absoluto.
Sin embargo, podemos decidir suponer que dado que aparecen tantos unos como se restan el resultado tiene que ser nulo:

Ahora bien, yo podría coger y modificar la forma de sumar de modo que cambiase el segundo término por el tercero, el cuarto por el quito y así hasta el infinito. Al hacer esto, por comparativa, podría concluir que la serie realmente suma 1:
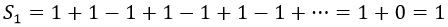
¿Pero por qué quedarme aquí?
Podría volver a hacer lo mismo, empezando en esta ocasión por cambiar de lugar el tercer miembro y el cuarto. Así obtendría un 2:
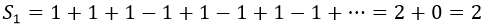
Por poder, podría incluso dividir todos los sumandos en sus dos mitades, reordenarlos por signos y después volver a cambiar el segundo por el tercero y demás.
Así obtendría 1/2:
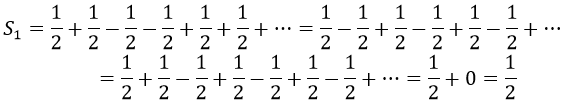
“¡Alto! ¡Te estás inventando números que antes no estaban!”, podría quejarse alguien. Nuestra intuición es incapaz de pensar en el infinito, de modo que cuando decimos que la suma total podría dar 0 inmediatamente pensamos en que el último sumando será un -1.
A partir de este razonamiento, los reordenamientos que he planteado estarían mal porque requerirían dejar un -1 extra como último sumando que no tendría pareja (sería el 1 de más que dejamos en el frente).
Sin embargo, los infinitos no funcionan así. No hay un “último” término de la serie.
Los reordenamientos que he hecho son, en cierto sentido, no tramposos.
La única trampa que hay aquí es haber intentado fijar un valor para una serie divergente.
Al fijar un valor, hemos visto inmediatamente que podemos falsearlo reordenando la serie y viendo que es incompatible con otras formas de sumarla. Las series divergentes, a priori, no tienen ningún valor, y carece de sentido intentar dárselo.
Hemos demostrado por fuerza bruta el teorema “troll” de las series divergentes: “Dada una serie divergente a la que podamos asignar un valor ordenándola de una forma concreta (condicionalmente convergente), podemos reordenarla como queramos para justificar que suma lo que nos dé la gana”.
¿Y ya está? ¿Con esto justificamos que la suma de los naturales no dé infinito? No, porque todavía no la hemos ordenado de ningún modo que justifique asignarle valor alguno.
Pero sigamos avanzando.
La sumación de Cesàro:
La sumación de Cesàro, un criterio para asignar un valor a una serie infinita bastante intuitivo, sugiere que si una serie converge a un valor, entonces dicho valor es la media de todas las sumas parciales de sus términos.
La suma parcial n-ésima Sn, por ejemplo, sería sumar solo los n primeros términos de una serie dada. Las sumas parciales de a1n son:
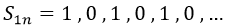
Esta sucesión de sumas parciales puede ser analizada por separado con el nombre de a2 y también tendría sus sumas parciales:

La sucesión S2n, a diferencia de S1n, converge para valores elevados de n de forma que:
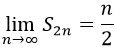
En particular, esta forma es exacta para todos los pares.
El criterio de Cesàro para obtener el valor S de una serie en función de sus sumas parciales Si sería:

Con lo cual, según Cesàro, la serie S1 daría como resultado:
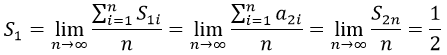
Este es uno de los muchos resultados posibles que habíamos obtenido.
No obstante, cabe destacar que este no “es” el valor de la serie dado que Cesàro solo habló de cómo definiría él el resultado de una serie convergente.
Uno puede discrepar con su criterio de sumación porque es lo que es: un criterio.
De hecho, si nos ponemos rigurosos, podríamos decir que su criterio no debería aplicarse en series divergentes.
La suma de todos los enteros a partir del resultado de Cesàro:
El título de esta sección es un poco engañoso, dado que no será “a partir de” sino que de nuevo haremos trampas reordenando cosas.
Definamos la sucesión a3 y su serie S3:
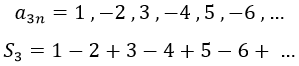
Podemos reescribir ahora S1 de una forma un poco rebuscada, que consiste en cambiar todos los unos por la resta entre el entero n y su anterior, lo que daría como resultado:

Aquí, si nos fijamos, podemos ver que tenemos todos los impares sumando dos veces y todos los pares restando otras dos.
Es decir, el doble de la serie S3. Con lo cual podemos imponer que S3 converge a 1/4:

Por otra parte, podemos considerar la serie S de todos los naturales y restarle S3.
El resultado sería cuatro veces S:
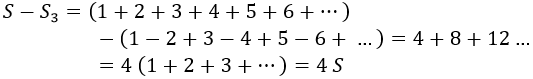
Y, ¡voilà!, ¡tenemos que todos los naturales suman -1/12!
Tras hacer ochenta pasos de dudosa validez, pero lo tenemos:
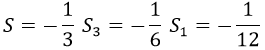
¿No estás contento? Pues veamos otra forma de obtenerlo que coincide.
La extensión analítica de series de Taylor:
Consideremos la expansión en serie de potencias de la siguiente función:
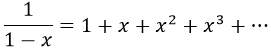
Por su forma, es evidente que la serie de potencias no puede funcionar cuando x vale 1 o más y, de forma análoga por simetría de la convergencia, tampoco cuando vale -1 o menos.
Sin embargo, es posible extender analíticamente la función de forma que este detalle logístico nos de igual e imponer que la igualdad es cierta para cualquier valor de x.
Bajo esta consideración, el valor de la función cuando x vale 1 seguiría siendo infinito, pero por la otra parte con -1obtendríamos que:
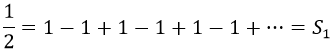
¡Hemos obtenido el mismo resultado que por el método de Cesàro! En principio por casualidad, pero lo hemos obtenido.
Extender el criterio de Cesàro para series divergentes y extender el teorema de Taylor fuera de su rango de convergencia asociado dan lugar al mismo resultado.
Elevemos ahora la ecuación al cuadrado y, de nuevo, no pasemos de la tercera potencia de x en la parte de la derecha:
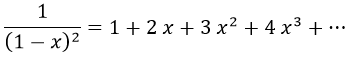
¿Y qué sucede si ahora volvemos a aplicarla en el caso de que x valga -1?

Otra coincidencia inesperada, ¿no?
Uno podría estar al borde de la emoción pensando en que al forzar que la serie genere S este método dará como resultado -1/12. Sin embargo, aquí nos vamos a llevar un pequeño disgusto, pues al sustituir que x valga 1 obtenemos una divergencia:
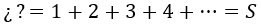
Sí, ya sé que ahí no va un interrogante sino un infinito atendiendo a la ecuación. Pero vamos a dejarlo así para ser más manipuladores si cabe.
Para poder evadir el infinito recurriremos a otra expresión matemática que en principio no fue diseñada para jugar con estas cuentas.
La función zeta de Riemann:
La función zeta se define del siguiente modo:
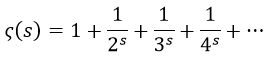
En principio fue definida para valores de s estrictamente mayores que 1, pero Riemann decidió extender su análisis a cualquier número complejo, donde se rodeaba dicha divergencia en el plano complejo gracias a los valores imaginarios.
Sobre variable compleja tendré que hablar más adelante en algún momento.
Una vez extendida la definición de la función zeta, cabe destacar que está estrechamente relacionada con S, dado que coinciden cuando s vale -1:
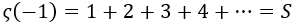
Dividamos la función zeta por 2 elevado a s.
Obtenemos:

Fijándonos en que obtenemos la propia zeta menos el primer término, podríamos usar este resultado para decir que:
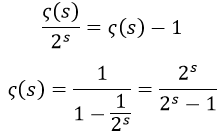
Y usando esto, podríamos sustituir s y obtener:
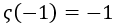
Uno podría realmente verse muy tentado de hacer tal cosa.
Sin embargo, estaría MAl. ¿Por qué?
Por lo que hemos visto en la segunda sección de esta entrada: hemos reordenado la misma serie al hacer la asignación y eso está prohibido.
Si queremos que las cosas queden “coherentes” debemos concretar una forma de ordenar exclusiva y no buscar otras por el camino.
Sí que estaría permitido, sin embargo, hacer la siguiente operación:
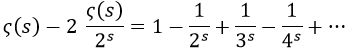
Y teniendo esto, cuando s valiese -1 podríamos usar la extensión analítica para fijar que:
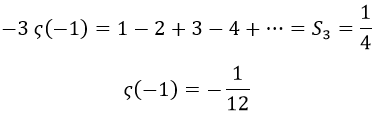
Que es lo que queríamos obtener. De modo que finalmente parece que no es tan descabellado trabajar con la igualdad:
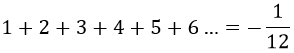
Conclusiones:
Si bien hemos hecho “trampa” y lo hemos reconocido, parece que las extensiones analíticas de la serie de Taylor, la forma más cómoda de intentar asignar valores a ciertas series condicionalmente convergentes, asignan valores concretos a las mismas.
En principio dichos valores rompen con todo lo esperable de una suma:
¿cómo voy a obtener un número fraccionario y negativo sumando naturales?
Sin embargo, en tanto que la serie ha de ser infinita para que se cumpla la igualdad podemos decir que no hay ningún paso discreto “bruto”.
De hecho, en algunos aspectos de la mecánica cuántica, parece que la naturaleza opta por sumar series divergentes usando la zeta de Riemann y sus pintorescos resultados, con lo que la propia naturaleza estaría fijando la forma adecuada de sumar series condicionalmente convergentes.
En el mundo de las matemáticas esto no tendría sentido, pero nadie obliga a la naturaleza a respetar los teoremas de la matemática.
Si quiere sumar de una forma concreta reordenando: puede.
Por supuesto, también puede ser que las teorías cuánticas que usan este tipo de apaño para reducir series divergentes sean erróneas y simplemente hayamos descubierto que en todos los sitios donde la cuántica se equivoca de este modo debería haber aparecido alguna zeta de Riemann.
Pero por lo pronto, y mientras no haya ninguna teoría que lo analice de otra forma, parece que las series divergentes y la zeta de Riemann guardan una estrecha relación, con todo lo que ello conlleva.