Una amiga, a raíz de ver la película “El efecto mariposa” me preguntó como podía interpretarse la película en términos de la mecánica cuántica.
La pregunta es interesante porque, al fin y a la postre, uno de los alicientes de las películas de ciencia ficción es intentar especular sobre la parte científica que normalmente sólo se suele esbozar, y generalmente de mala manera.
Aparte de la película había mas alicientes para pensar en el tema del tiempo en física dónde tenemos cosas como soluciones de la relatividad general que implican trayectorias que llevan hacia atrás en el tiempo (son sus consecuentes paradojas), taquiones, que, de existir, podrían enviar señales al pasado.

Bien, en la película tenemos un joven, estudiante de psicología, que a raíz de unos experimentos con bichos adquiere una habilidad para conseguir que cada vez que hay un aspecto trágico en su vida desencadenado de manera muy clara por un acontecimiento concreto es capaz de enlazar con una realidad en la que el acontecimiento sucedió de manera diferente y vivir las consecuencias de esa versión alternativa.
Supongo que los autores de la película pueden haberse inspirado en la interpretación de Everett de la mecánica cuántica en la que cada vez que se produce una medida cuántica hay una división de la realidad de tal forma que se forma un universo diferente para cada una de los posibles resultados de la medida.
Claramente eso lleva a intentar enfocar el tema del tiempo desde una perspectiva cuántica, y eso es lo que hice.
El punto de partida es a la vez sencillo y delicado.
Recordemos la base de la mecánica cuántica no relativista elemental.
Tenemos una función de onda  cuyo valor al cuadrado nos da la probabilidad de encontrar la partícula que representa esa función en el punto (x,y,z) en el instante t.
cuyo valor al cuadrado nos da la probabilidad de encontrar la partícula que representa esa función en el punto (x,y,z) en el instante t.
Aquí t es el tiempo “newtoniano” que existe de manera universal y es igual en cualquier punto del universo.
Por supuesto algo así no existe ya que la física Newtoniana debe ser sustituida por la de la relatividad general, en la cuál el tiempo forma parte de un cuadrivector.
Pero por ahora ignoremos esa parte relativista.
El planteamiento que hago es muy ingenuo, reinterpreto esa función de onda cómo la probabilidad de encontrar la función de onda en el punto (x,y,z) y, esta es la novedad, en el instante t.
Por supuesto tras esta propuesta ingenua a nivel de lenguaje se esconde una gran dosis de sutileza
¿Cómo es eso de no poder saber en que instante se encuentra la partícula?
Al fin y al cabo si estoy en un laboratorio tengo un reloj, y puedo saber en que momento he detectado la partícula.
Bien, tenemos el principio de incertidumbre de Heisenberg tiempo-Energía que afirma (más adelante entraré en las sutilezas de esta relación) que no podemos saber con total precisión a la vez el tiempo y la energía.
Pero, al fin y al cabo, si tenemos suficiente energía, podemos medir con precisión arbitraria el momento de la medida.
Definitivamente en el universo newtoniano la propuesta no tiene mucho sentido, y es necesario ya meter conceptos de relatividad dónde tenemos las transformaciones de Lorentz (relatividad especial) y, mas generalmente, el efecto de la masa cómo ralentizadora del paso del tiempo (el tiempo transcurre mas lento cerca de un cuerpo pesado que en el espacio libre).
En estas circunstancias no hay tiempo universal y debemos hablar de el tiempo propio relativista (asumo que todo el mundo conoce la paradoja de los gemelos y demás cosas típicas de la relatividad así que no daré explicaciones al respecto).  en relatividad especial, o, mas generalmente
en relatividad especial, o, mas generalmente 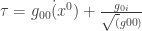 en relatividad general.
en relatividad general.
Bien, entonces, con el concepto de tiempo propio, ya tenemos un ingrediente para una forma posible (hay más) de interpretar eso de “probabilidad de hallar la partícula en el tiempo t”.
La otra cosa que necesitamos es el concepto de reloj cuántico.
Realmente es un concepto sencillo pero encontrar una forma rigurosa de exponerlo es ligeramente mas complejo.
La idea es tener un dispositivo que tenga una parte con un comportamiento periódico y otra que permita construir a partir de ese comportamiento un número que represente el tiempo transcurrido desde que el dispositivo empezó a funcionar.
Y, se supone, que ese chisme debe ser lo bastante pequeño para que los efectos cuánticos sean apreciables claro, que sino cualquier reloj convencional valdría.
Siendo un sistema cuántico compuesto de varias partículas lo vamos a poder representar por una función de onda conjunta 
Bien, aquí se supone que todas las partículas del reloj están en el mismo tiempo. Esto lo interpretamos cómo que no tenemos ningún dispositivo más pequeño que el propio reloj que nos permita medir el tiempo de manera separada para cada una de las partículas.
Asumimos, además, que las partículas del reloj se mantienen siempre confinadas en un volumen concreto (el tamaño del reloj) y que dentro de ese volumen el campo gravitatorio es aproximadamente constante.
En esas condiciones el reloj lo que hace es medir su propio tiempo propio, y ese t sería el  .
.
Con el tiempo propio, y el reloj cuántico para poder medirlo, ya podemos dar sentido a eso de “probabilidad de hallar la partícula (sistema cuántico) en el tiempo t).
Imaginemos que hacemos un experimento de doble rendija con nuestro reloj cuántico, pero con una pequeña variante.
Por una rendija el reloj viaja por un espacio-tiempo plano, por la otra pasa cerca de un miniagujero negro (o cualquier otra cosa lo bastante densa para introducir un retraso temporal que puede discernir el reloj cuántico). Obviamente si pasa por el espacio-tiempo plano el tiempo propio que le lleva al reloj llegar desde el punto de partida al final va a ser mayor que si pasa por la rendija cercana al microagujero negro.
Pero, claro, cómo en cualquier experimento de doble rendija no sabemos por dónde pasó exactamente el reloj cuántico y lo que tenemos es que en el resultado final vamos a encontrar que una vez medimos un valor t1 y otra un valor t2 (en realidad, si tenemos un microagujero negro, podríamos tener muchos valores posibles si al pasar por la rendija del agujero negro el reloj pudiera pasar por diferentes distancias al mismo).
Visto así, no podemos medir el tiempo propio y el tiempo no está determinado. Esta idea es un poco discutible ya que podría argumentarse que hay una cierta redundancia. Al fin y al cabo lo que tenemos es que la función de onda conjunta estaría en un estado de superposición entre dos de autovalores posibles que consideramos cómo “marca temporal”.
En realidad, como veremos, el “tiempo” normalmente va a ser una información menos detallada que un autoestado así que tal vez se podría obviar ese posible criticismo.
Aunque esta exposición de el concepto de reloj cuántico la he elaborado yo en su totalidad soy consciente de que hay mas gente que ha trabajado en esta idea y que incluso se ha hecho alguna implementación experimental de la idea.
Para poner un ejemplo concreto podríamos considerar que nuestro reloj cuántico fuese un conjunto pequeño de átomos con algunos electrones excitados en algún estado metaestable.
Con el paso del tiempo estos electrones irían decayendo al estado fundamental (el periodo de decaimiento al estado fundamental sería el ingrediente “periódico” del reloj) y podríamos usar el número de electrones medidos en el estado fundamental cómo “el tiempo transcurrido”.
Aquí hay varios autoestados compatibles con un número concreto de electrones en el estado fundamental (porque no nos importa en que núcleo concreto se ha producido la caída al estado excitado).
Es interesante el hecho de que aquí el tiempo es discreto, mientras que en física siempre es una variable continua. En teoría siempre podemos hacer un “reloj cuántico” mas preciso (al menos hasta llegar al tiempo de Planck, y según mucha gente incluso más allá) pero, en la práctica, podríamos argumentar que para estudiar nuestro sistema no podemos contar con mas información temporal que la que nos da el reloj cuántico mas preciso que tenemos.
La cosa se vuelve mas divertida cuando usamos estos relojes cuánticos en este tipo de casos para tomar medidas temporales de otros acontecimientos. Tomemos el caso de dos naves espaciales.
Uno viaja de A a B por una zona plana y otra cerca de un agujero negro.
Esas naves usan relojes atómicos para medir el tiempo.
Cómo esos relojes no tienen bien definido el tiempo cualquier evento lleva automáticamente indefinido el tiempo y así las funciones de onda que representen procesos cuánticos en esas naves no tendrían el tiempo bien definido.
Dejo al lector que rellene los detalles de experimentos concretos que ilustren de forma rigurosa esta idea, que no voy a hacerlo todo yo
.
Asumamos que lo explicado anteriormente se sostiene (es un tema abierto a discusión, claro).
En ese caso vamos a proceder a hacer un formalismo Naiver para añadir eso y crear nuestra “cronomecánica cuántica”.
Recordemos que en mecánica cuántica tenemos dos operadores fundamentales, el operador momento  y el operador posición
y el operador posición 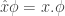 .
.
La justificación del operador x, básicamente, es la de obtener el valor mas probable de la posición, y eso en una variable estadística, es la media (osea, multiplicar por x y sumar/integrar x multiplicado por la distribución estadística, osea, la función de onda.
Otra gente interpreta ese operador cómo trasladar en una distancia x la función de onda, pero, la verdad, yo prefiero la interpretación probabilística.
Cómo quiera que se vea eso permite que, inmediatamente, el operador “posición temporal” sea multiplicar la función por t, i.e.  .
.
El operador análogo al operador momento es mas delicado.
El operador momento se interpreta cómo el generador infinitesimal de las traslaciones .
Entonces, podríamos decir que el operador “Cronos”  genera las traslaciones en el tiempo.
genera las traslaciones en el tiempo.
Si admitimos eso podríamos hallar las relaciones de conmutación entre los dos operadores y comprobar que son las mismas que entre los operadores x y p i.e. ![[\hat x, \hat p]= \hat x \hat p - \hat p \hat x= i\hbar [\hat x, \hat p]= \hat x \hat p - \hat p \hat x= i\hbar](https://s0.wp.com/latex.php?latex=%5B%5Chat+x%2C+%5Chat+p%5D%3D+%5Chat+x+%5Chat+p+-+%5Chat+p+%5Chat+x%3D+i%5Chbar&bg=ffffff&fg=333333&s=0) es decir
es decir ![[\hat t, \hat c]= i\hbar [\hat t, \hat c]= i\hbar](https://s0.wp.com/latex.php?latex=%5B%5Chat+t%2C+%5Chat+c%5D%3D+i%5Chbar+&bg=ffffff&fg=333333&s=0) .
.
Hasta aquí todo parece sencillo y sin sutilezas.
El problema surge cuando uno se da cuenta que ya hay un operador casi idéntico a lo que yo he llamado operador Cronos, el “operador energía” que es igual en todo excepto en el factor de 2m dividiendo.
Este “operador energía” aparece en la ecuación de Schröedinger dependiente del tiempo 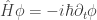 y en la ecuación de Klein-Gordon, dónde es mas evidente que juega el papel de la energía ya que ahí se toma la relación clásica entre el trimomento y la energía:
y en la ecuación de Klein-Gordon, dónde es mas evidente que juega el papel de la energía ya que ahí se toma la relación clásica entre el trimomento y la energía:  y se sustituye la E por el “operador energía” para obtener la ecuación de Klein-Gordon (para mas detalles ver en la wiki la Ecuación de Klein-Gordon.
y se sustituye la E por el “operador energía” para obtener la ecuación de Klein-Gordon (para mas detalles ver en la wiki la Ecuación de Klein-Gordon.
Esto del “operador energía”, cómo digo, es algo curioso.
Al fin y al cabo en mecánica cuántica la energía es el hamiltoniano.
Además, resolviendo la ecuación de Schröedinger dependiente del tiempo se puede ver que el hamiltoniano es lo que genera la evolución temporal del sistema cuántico, en analogía al operador momento que general la traslación espacial.
Resulta curioso también que el “operador energía” no incluya la masa. Mi “operador cronos” si incluye esa masa, y, formalmente, uno podría pensar que también debería generar las traslaciones en el tiempo.
Sobre la presencia o no de la masa se puede argumentar que en un sistema general la masa si influye y no evolucionan en el tiempo de la misma manera dos partículas de distinta masa (eso sólo pasa en el campo gravitatorio, pero no en, por ejemplo, un campo magnético) por lo cuál sería mejor “operador energía” mi operador cronos que el normal.
Por otro lado, si se hace eso, no se obtiene la ecuación de K-G.
Que el operador cronos se pudiera interpretar como una energía sería interesante porque aquí la incertidumbre tiempo-energía tendría la misma interpretación que en el caso de la posición y el momento.
Normalmente la relación de incertidumbre tiempo-energía, se interpreta cómo que en una transición entre dos estados separados por una energía E si queremos medir esa energía con una precisión dada necesitamos al menos un tiempo de observación que cumpla esa relación de incertidumbre.
Eso también lleva al concepto de partícula virtual en la que si no “miramos” durante un tiempo t se puede formar una partícula con energía E compatible mediante la relación de incertidumbre con el tiempo que estamos sin “mirar”.
Cómo, por supuesto, esta teoría no pretende ser totalmente seria no he examinado a fondo estos aspectos, tampoco he mirado otras temas de compatibilidad ¿conmutan estos operadores que he introducido con el hamiltoniano para poder ser observables?
En todo caso, asumiendo que hay una relación entre mi operador C y la energía podemos ir un poco más allá.
El operador C tiene, en general, espectro continuo con valores negativos y positivos, como el operador t. Eso vendría a interpretarse cómo que tenemos partículas yendo hacia delante y hacia atrás en el tiempo, y tendríamos una visión de las antipartículas cómo los autoestados negativos del operador C.
Una vez más no he analizado a fondo el asunto, y dejo en manos de alguien potencialmente interesado que lo haga si le apetece divertirse con un tema desenfadado cómo es este.
Una vez expuesto el “formalismo” de la cronomecánica cuántica vamos a aplicarlo a jugar un poco más con él.
Cuando tenemos algún caso de paradojas temporales, es decir, que viajamos por una curva de tiempo cerrada y partiendo de un tiempo t1 llegamos a un tiempo t2 dónde t2th a otro t1
Aquí ya tenemos un problema posible al intentar hacer superposiciones cuánticas ya que las partículas antes y después del th no son iguales.
Por ejemplo, un bosón vectorial Z tiene masa después de th y es de masa 0 antes de th.
Sí hacemos volver una partícula Z en el tiempo a través de una de esas curvas de tiempo cerrado tendríamos que considerar un estado de superposición entre una partícula sin masa y otra con masa, y con distintos grados de liberad además.
En realidad en cuántica de campos el observable es el campo y podríamos decir que en t
En cualquier caso eso de hacer superposiciones de estados que pertenecen a vacíos distintos es algo que se supone que está prohibido en cuántica por las reglas de superselección y no debería poder hacerse.
Entonces, si conectamos estados temporales dónde el vacío cuántico ha cambiado nuestro formalismo de superposición cuántica de estados ya no valdría y deberíamos buscar algo más sofisticado.

Otro tema mas divertido aún en esto de las paradojas temporales y la definición del tiempo es jugar con cuerdas.
Imaginemos que la teoría de cuerdas es correcta y que agarramos una cuerda elemental y la hacemos crecer hasta un cierto tamaño macroscópico (esto es algo que Witten argumentó que podría haber ocurrido en el periodo inflaccionario y tener cuerdas cósmicas que fuesen cuerdas elementales agrandadas en vez de las asociadas a rupturas de la simetría, que son el otro tipo de cuerdas cósmicas posibles).
Se supone que una cuerda tiene un tiempo bien definido.
Ahora bien, si extendemos una cuerda macroscópica en una curva de tiempo cerrada sus diversos puntos estarían, en general, en tiempos diferentes, y, si la hacemos girar, estaría mandando hacia atrás en el tiempo a una parte de si misma.
Por supuesto esto es un ejemplo muy tramposo porque el propio campo gravitatorio de esta cuerda cósmica fundamental seguramente sería lo bastante intenso para romper la geometría que permite la existencia de esas curvas de tiempo cerradas.
En realidad existe algo llamado el principio de protección cronológica, introducido por Hawking, que argumenta (pero no demuestra) que siempre va a haber efectos cuánticos que arruinan la geometría clásica con curvas de tiempo cerradas.
En su libro de agujeros de gusano Matt Visser hace un cálculo de teoría cuántica de campos que demuestra (al menos en buena parte) que esos efectos cuánticos destruyen el agujero de gusano cuando este intenta usarse cómo máquina del tiempo.
Otras cosa que, por ejemplo, se podría considerar con este formalismo que he introducido es ¿que pasa con el operador de ordenación temporal en teoría cuántica de campos?
Y bastantes otras cosas (he considerado unos cuantos aspectos más, pero me llevaría demasiado espacio discutirlos).
En cualquier caso, la verdad, no creo que el tema merezca meterse en tantas profundidades.
Considero este "formalismo" cómo una guía práctica para tratar con algo de sentido, y un criterio concreto, las paradojas temporales que le gusta analizar a la gente de CF y poco más.
Pero si alguien quiere profundizar en el tema y exprimir más el formalismo libre es.