lunes, 18 de abril de 2011

Pfaffiano de una matriz antisimétrica


DERIVATION FROM DETERMINANT


WE ASSUME THAT N IS AN EVEN NUMBER AND

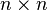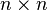 A = (AIJ) IS AN n \times n SKEW-SYMMETRIC MATRIX.
THE PFAFFIAN OF A CAN BE DERIVED AS FOLLOWS.

 USING THE LAPLACE'S FORMULA WE CAN WRITE DET(A)
AS

\det(A) = \sum_j a_{ij}C_{ij}, \,

WHERE CIJ = ( − 1)I + JDET(AIJ) IS THEIJTH COFACTOR OF A AND AIJ IS THEIJTH MINOR OF A. BY THE ADJUGATEFORMULA, WE HAVE

\det(A \times \mathrm{adj}(A))=\det(A)^n. \,

WE HAVE
\det\left( \begin{array}{cccc}1&0&\cdots&0\\ 0&1&\cdots&0\\ a_{31}&a_{32}&\cdots&a_{3n}\\ \cdots&\cdots&\cdots&\cdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}\end{array} \right) \times \det \left( \begin{array}{cccc}C_{11}&C_{21}&\cdots&C_{n1}\\ C_{12}&C_{22}&\cdots&C_{n2}\\ C_{13}&C_{23}&\cdots&C_{n3}\\ \cdots&\cdots&\cdots&\cdots\\ C_{1n}&C_{2n}&\cdots&C_{nn}\end{array} \right) = \det\left( \begin{array}{cc} C_{11}&C_{21}\\C_{12}&C_{22}\end{array} \right) \det(A)^{n-2},

THUS

\det(A_{12, 12})\det(A)^{n-1} = \det \left( \begin{array}{cc} C_{11} & C_{21}\\ C_{12} & C_{22} \end{array} \right) \det(A)^{n-2},

WHERE A_{12, 12} \, IS THE (n-2) \times (n-2)MINOR OF A OBTAINED BY DELETING THE FIRST TWO ROWS AND THE FIRST TWO COLUMNS OF A. 

OF COURSE, IT IS ARBITRARY THAT WE HAVE CHANGED THE FIRST TWO 
ROWS IN THE ABOVE EQUATION. IN GENERAL WE HAVE
C_{ii}C_{jj} - C_{ij}C_{ji} = \det(A_{ij,ij})\det(A), \,

SO FAR WE HAVE NOT USED THE ASSUMPTION THAT N IS EVEN AND A IS SKEW-SYMMETRIC. WITH THAT, SINCE AIIIS AN (n-1)\times(n-1) SKEW-SYMMETRIC MATRIX AND (N − 1) IS ODD, CLEARLYDET(AII) = 0
 AND HENCE CII = 0. SIMILARLY CJJ = 0. ON THE OTHER HAND,

C_{ij} = (-1)^{n-1}C_{ji} = -C_{ji}. \,

SO THE ABOVE EQUATION IS SIMPLIFIED AS

C_{ij} = (-1)^{i+j}\sqrt{\det(A_{ij,ij})\det(A)}. \,.

WE NOW PLUG THIS BACK INTO THE ORIGINAL FORMULA FOR THE DETERMINANT,

\det(A) = \sum_j a_{ij}(-1)^{i+j}\sqrt{\det(A_{ij,ij})\det(A)}, \,

WHICH YIELDS
\sqrt{\det(A)} = \sum_j a_{ij}(-1)^{i+j}\sqrt{\det(A_{ij,ij})}. \,

LA APROXIMACIÓN DE HARTREE-FOCK-BOGOLIUBOV (HFB)
 SE UTILIZA EN FÍSICA CUÁNTICA PARA APROXIMAR 
EL COMPORTAMIENTO DE UNA PARTÍCULA SUJETA AL EFECTO 
DE MUCHAS OTRAS PARTÍCULAS COMO SI ESTAS GENERARAN
 UN CAMPO PROMEDIO EFECTIVO.
DE ESTA MANERA SE EVITA TENER QUE CONSIDERARLAS 
DE FORMA INDIVIDUAL.
LA APROXIMACIÓN FUE INTRODUCIDA POR D.R. HARTREE
 EN 1928 Y POR V.A. FOCK EN 1930 , AUNQUE SE CONVIRTIÓ
 EN UNA HERRAMIENTA FUNDAMENTAL TRAS EL TRABAJO 
DE N.N. BOGOLIUBOV EN 1958 .
CUANDO SE REQUIERE UN RESULTADO MÁS PRECISO, 
HAY QUE APLICAR LA APROXIMACIÓN HASTA SEGUNDO ORDEN, 
LO QUE REQUIERE COMBINAR Y SOLAPAR LAS FUNCIONES
 DE ONDA DE LA APROXIMACIÓN HFB A PRIMER ORDEN.
EL SIGNO DEL SOLAPE REQUIERE EVALUAR UNA RAÍZ CUADRADA.
EL PROBLEMA ES SABER QUÉ SIGNO TIENE QUE 
SER UTILIZADO PARA ESTA RAÍZ CUADRADA.
EN ALGUNOS PROBLEMAS (EN LOS QUE HAY SIMETRÍAS
 DISCRETAS) EL RESULTADO ES INDEPENDIENTE DEL SIGNO 
(NO IMPORTA EL QUE SEA).
PERO EN OTROS PROBLEMAS (EN LOS QUE ESTAS SIMETRÍAS 
ESTÁN ROTAS) LA APROXIMACIÓN NO DICE QUÉ SIGNO USAR.
EL SIGNO HA DE SER CALCULADO UTILIZANDO OTRA TÉCNICA.
PODEMOS UTILIZAR UNA TÉCNICA MUY ELEGANTE 
(QUE SE BASA EN EL USO DE ESTADOS COHERENTES 
FERMIÓNICOS) CON LA QUE LOGRA DETERMINAR EL SIGNO
 DEL TÉRMINO DE SOLAPE SIN NINGUNA AMBIGÜEDAD.
EL SIGNO DEPENDE DEL PFAFFIANO
 DE UNA MATRIZ ANTISIMÉTRICA.
LA NUEVA TÉCNICA ES MUCHO MÁS EFICIENTE Y SENCILLA 
DE APLICAR QUE OTRAS TÉCNICAS ALTERNATIVAS,
 SIN NECESIDAD DE RECURRIR AL USO DE MATRICES
 NO HERMÍTICAS.
EL NUEVO RESULTADO TIENE MÚLTIPLES APLICACIONES,
 COMO EL USO DE LA APROXIMACIÓN HFB PARA EL ESTUDIO
 DE LA DINÁMICA DE PROTONES O NEUTRONES
 EN NÚCLEOS ATÓMICOS CON NÚMERO ATÓMICO IMPAR
 (LA SUMA DEL NÚMERO DE PROTONES Y NEUTRONES).

Publicado por en

No hay comentarios:

Publicar un comentario