He tratado de encontrar cuál era la motivación de Riemann a la hora de proponer que los ceros de la función zeta se encuentran en la línea crítica y lo he hecho recurriendo a la historia, avanzando hasta Ramanujan, reculando hasta Galois, repasando a Hardy, admirando a Euler y en resumen recorriendo los senderos transalgebraicos entre el análisis en variable compleja y la teoría de números algebraicos.
Discurso fluido, sincero y escéptico que me ha llevado a recomendar a los jóvenes lo mismo que se recomendaba John F. Nash a sí mismo:
nunca confíes en los surveys sobre la conjetura de Riemann, todos están equivocados, no ha habido progresos hacia la demostración de la conjetura desde hace muchas décadas.
Ni Deligne, ni Bombieri, ni santas pascuas (y no digamos nada de De Branges, Connes y otros “aficionados al bombo”).
Debemos ser honestos y confesar que ni tenemos ni idea sobre el camino para demostrar la hipótesis de Riemann ni tenemos ni idea sobre su significado transalgebraico.
¡Me ha gustado la palabra“transalgebraico”!
¿cuál es la gran diferencia entre π² y π³?
O en general, entre una potencia par de π
y una potencia impar de este número.
La diferencia ya la conocía Euler y desde entonces, no se ha avanzado nada al respecto.
¿Cuál será? π² es un número transalgebraico que tiene una función entera minimal  .
.
Esta función entera minimal equivale al polinomio mínimo asociado a todo número algebraico.
Nadie sabe cuál es la función entera minimal de π, ni de cualquiera de sus potencias impares; además debería ser tan sencilla que si no conoce es porque no existe.
Si quieres saber más al respecto, te recomiendo la lectura de sus notas
“La hipótesis de Riemann.”
¿Aproximaciones físicas a la hipótesis de Riemann?
Son otro callejón sin salida.
La función zeta de Riemann es tan sencilla (transalgebraicamente hablando) que si modela un sistema físico éste tiene que ser tan sencillo que ya habría sido descubierto y la hipótesis de Riemann habría sido probada.
Como no se ha dado lo segundo, lo primero no implica ningún
tipo de progreso.
Aún así, y como yo soy físico, me gustaría recordar que la función zeta de Riemann aparece en muchos problemas de física, desde la mecánica clásica a la física de la materia condensada.
A los interesados les recomiendo el interesante artículo de Daniel Schumayer, David A. W. Hutchinson, “Physics of the Riemann Hypothesis,” Review of Modern Physics 83: 307-330, 2011 [gratis en ArXiv].
¿Estás interesado en la hipótesis de Riemann?
Deberías empezar leyendo a Aleksandar Ivić, “On some reasons for doubting the Riemann hypothesis,” ArXiv, 11 Nov 2003 ["creer o no creer en la validez de la hipótesis de Riemann, that's the question!"].
Y ni se te ocurra leer a Enrico Bombieri en su descripción del problema del Milenio (“The Riemann hypothesis,” porque dicen que la mejor manera de provocar que toques algo es poner un cartel que diga que no lo toques).
¿Qué deberías leer entonces?
E. Landau, 2Handbuch der Lehre von der Verteilung der Primzahlen,” 2nd Edition, Chelsea, New York, 1953, y a H. M. Edwards, “Riemann’s Zeta Function,” Dover Publications, New York, 2001.

La hipótesis de Riemann
Los números primos  son los números naturales
son los números naturales  que no son divisibles salvo por ellos mismos y por la unidad.
que no son divisibles salvo por ellos mismos y por la unidad.
Hay infinitos primos, pero los detalles de su distribución aún están ocultos. Euler demostró con 1737 que
lo que indica que los números primos son muy frecuentes entre los números naturales; recuerda que
Euler fue más allá y demostró usando el teorema fundamental
de la aritmética que
expresión matemática bien definida para  .
.
La función  no tiene ceros reales para
no tiene ceros reales para  .
.
Bernhard Riemann aplicó las herramientas del análisis en variable compleja
a la función zeta y la extendió a todos los números complejos como
función que puede ser continuada analíticamente para todo el plano complejo  excepto para
excepto para  .
.
Esta función de variable compleja  ,
,
donde 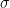 y
y 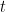 son números reales, y
son números reales, y  , es la llamada función zeta
, es la llamada función zeta
de Riemann y presenta cierta simetría alrededor de la línea crítica
dada por la ecuación funcional
que permite demostrar que tiene ceros (llamados triviales) en todos los
números enteros negativos  .
.
Además, si la función tiene un cero  , con
, con  también tendrá como cero el número simétrico con
también tendrá como cero el número simétrico con 
y sus dos simétricos respecto al eje 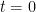 .
.
Riemann conjeturó como hipótesis razonable que todos los ceros no triviales de la función  son de la forma Es=1/2, es decir, se encuentran en la línea crítica.
son de la forma Es=1/2, es decir, se encuentran en la línea crítica.
En 1900, Hilbert consideró la hipótesis de Riemann como el octavo problema de su famosa lista, y de ahí acabó como uno de los problemas del milenio
del Instituto Clay de Matemáticas dotado con un millón de dólares.
Durante el s. XX ha habido ciertos avances menores en la demostración
de la conjetura, como cuando Hardy demostró en 1914 que hay infinitos ceros de la función  en la línea crítica, pero esto no basta para demostrar
en la línea crítica, pero esto no basta para demostrar
la hipótesis de Riemann (hoy sabemos gracias a Conrey, 1989, que al menos dos tercios de los ceros se encuentran en ella).
Todos lo ceros deben estar en ella.
Y no digo más al respecto… porque no quiero que leas a J. Brian Conrey,
“The Riemann Hypothesis,” Notices of the AMS, March 2003.
No hay comentarios:
Publicar un comentario