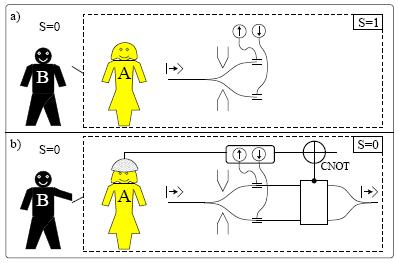
Experimento mental: (a) Alicia en un laboratorio aislado realiza una medida de Stern-Gerlach produciendo un bit de entropía (para ella, no para Bernardo). (b) Bernardo "cancela" la medida de Alicia por decorrelación y la entropía para Alicia se reduce (no así la entropía total) pero ella no puede "recordar" que alguna vez hubiera crecido.
Lorenzo Maccone afirma en “Quantum Solution to the Arrow-of-Time Dilemma,” Phys. Rev. Lett. 103: 080401, 21 Aug. 2010 [gratis en ArXiv], haber resuelto la paradoja de Loschmidt:
¿cómo surge la flecha del tiempo termodinámica en un universo
cuya física es reversible?
¿Cómo surge la segunda ley de la termodinámica que afirma
que la entropía siempre crece?
La definición clásica de la entropía no permite resolver la paradoja.
Maccone utiliza la definición de entropía (cuántica) de von Neumann en la que el observador juega un importante papel.
La ”memoria” del observador recuerda solamente la física compatible
con la segunda ley de la termodinámica.
Las violaciones de dicha ley se pueden dar pero son “olvidadas”
por el observador.
Las ideas de Maccone recuerdan a las de Roger Penrose y otros que ven
en el proceso de medida cuántica la irreversibilidad que conduce a la segunda ley de la termodinámica.
“I show that entropy in a system can both increase and decrease
(as time reversal dictates), but that all entropy-decreasing transformations cannot leave any trace of their having happened.
Since no information on them exists, this is indistinguishable from the situation in which such transformations do not happen at all: ‘‘The past exists only insofar as it is recorded in the present.’’ Then the second law is forcefully valid: the only physical evolutions we see in our past, and which can then be studied, are those where entropy has not decreased.”
[Palabra de Lorenzo Maccone].
Hay que empezar recordando la definición de entropía de von Neumann (recordatorio de cualquier curso de mecánica estadística cuántica).
Hay varias formulaciones equivalentes entre sí de la mecánica cuántica,
cada una de las cuales tiene sus ventajas en ciertos problemas
y sus inconvenientes en otros.
Una de ellas es la basada en matrices de densidad que nos permite estudiar sistemas microscópicos y mesoscópicos con el mismo formalismo,
es decir, nos permite modelar fácilmente un conjunto de sistemas
cuánticos en interacción.
La matriz de densidad cumple versión cuántica de la ecuación de Liouville
de la mecánica clásica estadística.
La ecuación de Liouville-von Neumann es ![\mbox{i}\,\hbar\,\partial\rho/\partial t = [H,\rho]](http://s0.wp.com/latex.php?latex=%5Cmbox%7Bi%7D%5C%2C%5Chbar%5C%2C%5Cpartial%5Crho%2F%5Cpartial+t+%3D+%5BH%2C%5Crho%5D&bg=ffffff&fg=000000&s=0 "\mbox{i}\,\hbar\,\partial\rho/\partial t = [H,\rho]")
,
, donde el operador densidad es el equivalente cuántico de la función
de distribución de probabilidad.
La entropía de von Neumann de un sistema cuántico se define
como ![S(\rho)\equiv-\mbox{Tr}[\rho\,\log_2\rho]](http://s0.wp.com/latex.php?latex=S%28%5Crho%29%5Cequiv-%5Cmbox%7BTr%7D%5B%5Crho%5C%2C%5Clog_2%5Crho%5D&bg=ffffff&fg=000000&s=0 "S(\rho)\equiv-\mbox{Tr}[\rho\,\log_2\rho]")
.
. En los sistemas en los que se pueden definir tanto la entropía clásica como
la entropía de von Neumann, ambas entropías coinciden
(módulo una constante multiplicativa sin importancia).
Por supuesto, hay sistemas en los que solo es aplicable la entropía cuántica.
“Entropy can decrease, but its decrease is accompanied by an erasure of any memory that the entropy-decreasing transformation has occurred.” [Palabra de Lorenzo Maccone].
Cualquier interacción entre dos sistemas 
y 
que haga decrecer la entropía en una cierta cantidad de bits debe reducir la información mutua cuántica
y 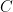que haga decrecer la entropía en una cierta cantidad de bits debe reducir la información mutua cuántica en la misma cantidad de bits, salvo que dicha entropía se acumule en cierto reservorio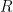 
.
. La información mutua cuántica mide la cantidad de información que correlaciona dos sistemas cuánticos, sean y , definiéndose como
y 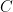, definiéndose como
, donde 
es el estado del sistema conjunto 
, y 
y 
los estados de y por separado.
es el estado del sistema conjunto , y y 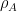los estados de y 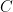por separado. El resultado fundamental del artículo de Lorenzo Maccone, que la reducción de entropía implica un efecto de borrado de la memoria del estado inicial del sistema, se escribe mediante la fórmula matemática
, (1)donde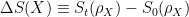 
es la diferencia de entropía entre el estado final (en el momento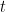 
)
) y el estado inicial para el sistema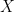 
, y 
.
, y 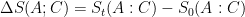. No entraré en los detalles de la demostración (muy sencilla, por otra parte).
La interpretación de esta fórmula es que el efecto de borrado de la memoria proviene de la pérdida de información mutua cuántica.
La memoria de un suceso es un sistema físico que tiene una información mutua clásica no nula de un sistema .
que tiene una información mutua clásica no nula de un sistema 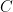. El borrado de la memoria de este suceso se produce al eliminarse
la información cuántica mutua 
, ya que esta última cantidad
, ya que esta última cantidad es una cota superior de la información mutua clásica 
(omito la demostración, también sencilla).
La interpretación de la ecuación (1) es que, si queremos disminuir la entropía de los sistemas y sin incrementar la entropía del reservorio ,
y 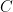sin incrementar la entropía del reservorio 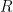, es necesario reducir la información mutua cuántica entre los sistemas y .
y 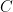. En la figura que abre esta entrada, un experimento mental, el sistema
es el laboratorio de Alicia y el sistemas 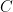es una partícula de espín 1/2:
es una partícula de espín 1/2: sus entropía finales se reducen en un bit a costa de borrar dos bits
de información mutua cuántica 
.
.La ecuación (1) nos dice que tomando como sistema al observador,
al observador, Alicia, y su laboratorio, y considerando un tiempo intermedio en el que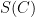 
es mayor que en los momentos inicial y final, debido a alguna transformación que incremente la entropía sin que sea absorbida por el reservorio ,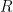
, ésta se puede reducir mediante una transformación que decremente
la entropía a costa de reducir la información mutua entre el observador
y el sistema observado .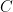
. Incluso si la entropía 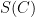, medida desde el punto de vista del observador, decrece, el observador no será consciente de ello, ya que la transformación que decrece la entropía debe factorizar (separar) el observador y el sistema que contienen información del suceso que incrementó con anterioridad
, medida desde el punto de vista del observador, decrece, el observador no será consciente de ello, ya que la transformación que decrece la entropía debe factorizar (separar) el observador y el sistema 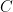que contienen información del suceso que incrementó con anterioridad su entropía.
La memoria de tal evento (que decrece la entropía) será parte
de las correlaciones que se destruirán.
Un resultado directo de la regla de Born aplicada al entrelazamiento
entre observador y sistema observado
(un proceso mecánico cuántico irreversible).
No hay comentarios:
Publicar un comentario