Introducción
La cuadratriz es una curva descubierta por los antiguos matemáticos griegos que resuelve dos de los problemas famosos de la época: la trisección del ángulo y la cuadratura del círculo.
No sabemos quienes descubrieron sus propiedades,
pero autores antiguos la asocian con Dinóstrato, Nicomedes e Hipias.
En el libro IV de la ‘Colección Matemática’ de Pappus de Alejandría nos ha llegado una demostración de la propiedad de la cuadratriz que permite cuadrar el círculo, que presentamos aquí.
Usamos la notación  para expresar ‘
para expresar ‘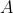 es a
es a 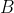 como
como  es a
es a  ’,
’,
en lugar de la notación de igualdad de fracciones, para intentar acercarnos a los conceptos de las antiguas matemáticas griegas.
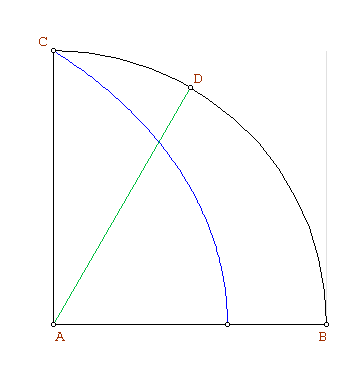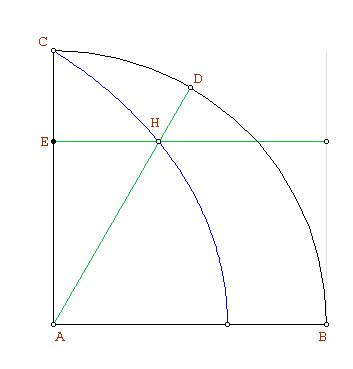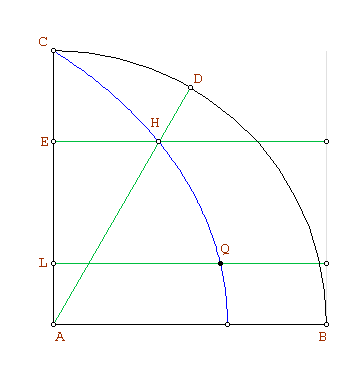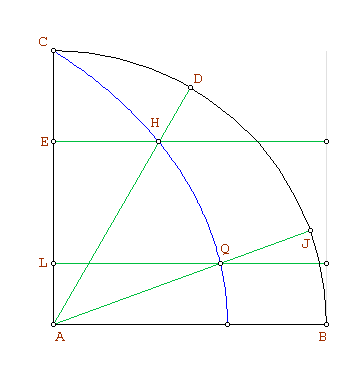
Generación de la cuadratriz
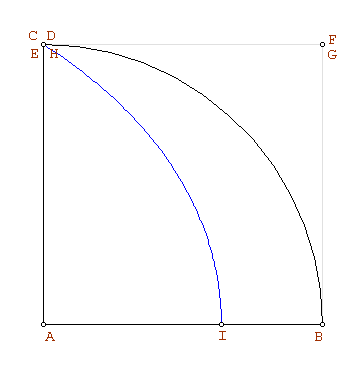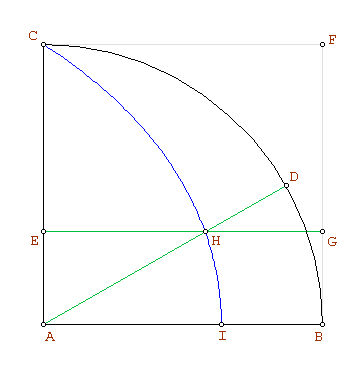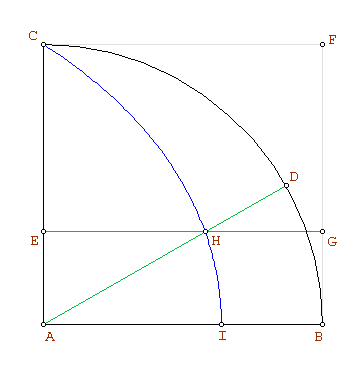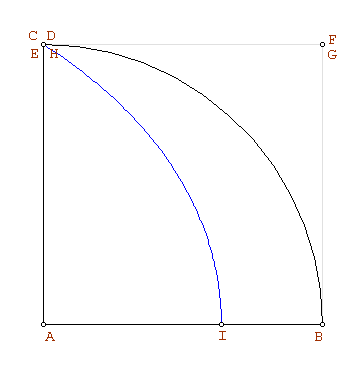
Supongamos inscrito en el cuadrado  un arco de circunferencia
un arco de circunferencia  con centro
con centro 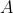 . Sea
. Sea  un punto que parte de
un punto que parte de  y se desplaza por el arco
y se desplaza por el arco  a velocidad uniforme. Sea
a velocidad uniforme. Sea 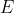 un punto que parte de
un punto que parte de  en el mismo momento que
en el mismo momento que  y se desplaza por el segmento
y se desplaza por el segmento  a velocidad uniforme y de forma que el tiempo en que
a velocidad uniforme y de forma que el tiempo en que  recorre
recorre  es el mismo que el tiempo en que
es el mismo que el tiempo en que  recorre el arco
recorre el arco  . Entonces, en cada instante, la longitud del segmento
. Entonces, en cada instante, la longitud del segmento  es a la longitud del segmento
es a la longitud del segmento  como la longitud del arco
como la longitud del arco es a la longitud del arco
es a la longitud del arco  , lo que expresamos con la notación
, lo que expresamos con la notación  . El punto
. El punto  , en que se cortan la perpendicular a
, en que se cortan la perpendicular a  por
por  y la recta
y la recta , describe la curva llamada cuadratriz.
, describe la curva llamada cuadratriz.
Como con regla y compás podemos bisecar ángulos y obtener el punto medio de segmentos, podemos obtener con regla y compás puntos de la cuadratriz tan cercanos entre sí como queramos.
La división del ángulo
La cuadratriz permite inmediatamente dividir un ángulo en la misma proporción que un segmento y viceversa, es decir, reduce el problema de la división de un ángulo al de la división de un segmento. Se presume que éste fue el uso para el que se inventó en primer lugar la cuadratriz.
Si queremos dividir un ángulo  según una razón dada
según una razón dada  , obtenemos el punto
, obtenemos el punto  de intersección del ángulo con la cuadratriz, y a continuación el punto
de intersección del ángulo con la cuadratriz, y a continuación el punto 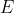 con
con  perpendicular a
perpendicular a  . Obtenemos en
. Obtenemos en  un punto
un punto  de forma que
de forma que  (Elementos VI.9) y a continuación el punto
(Elementos VI.9) y a continuación el punto 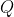 , intersección de la cuadratriz con la perpendicular a
, intersección de la cuadratriz con la perpendicular a  por
por  . Por último obtenemos el punto
. Por último obtenemos el punto 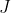 , interseccion de
, interseccion de  con el arco
con el arco  .
.
Como por la definición de la cuadratriz  y
y  , resulta que
, resulta que  , y hemos dividido el ángulo
, y hemos dividido el ángulo  en la razón
en la razón  requerida.
requerida.
La cuadratura del círculo
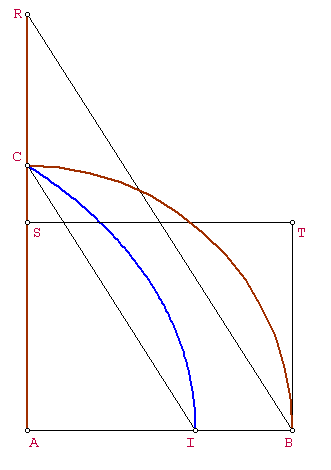
Si primero se concibió la cuadratriz para dividir ángulos, quizá fue una sorpresa descubrir que también resolvía el problema de la cuadratura del círculo. Para ello no hace falta la cuadratriz, sino solo el punto 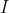 de intersección de la cuadratriz con la base
de intersección de la cuadratriz con la base  . Ese punto
. Ese punto 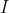 no se produce como intersección de las rectas
no se produce como intersección de las rectas y
y  en la primera figura, porque esas rectas coinciden cuando llegan a
en la primera figura, porque esas rectas coinciden cuando llegan a 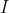 , y por tanto tenemos que definirlo como el punto límite al que tienden los puntos de la cuadratriz cuando
, y por tanto tenemos que definirlo como el punto límite al que tienden los puntos de la cuadratriz cuando  y
y  se acercan a
se acercan a  .
.
La propiedad del punto 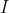 que permite rectificar la circunferencia y cuadrar el círculo es que
que permite rectificar la circunferencia y cuadrar el círculo es que  , o, dicho en palabras, la longitud del arco
, o, dicho en palabras, la longitud del arco  es a la longitud del segmento
es a la longitud del segmento  como la longitud del segmento
como la longitud del segmento  es a la longitud del segmento
es a la longitud del segmento  .
.
Ello implica que si 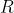 es la intersección de la paralela a
es la intersección de la paralela a  que pasa por
que pasa por 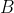 con la prolongación de
con la prolongación de  , la longitud
, la longitud  es igual a la longitud del arco
es igual a la longitud del arco  (porque
(porque  ).
).
Entonces, puesto que el área de un sector circular es la mitad de la longitud del arco por el radio, si 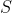 es el punto medio de
es el punto medio de  , el área del sector circular
, el área del sector circular  es igual al área del rectángulo
es igual al área del rectángulo  . Por tanto el área del círculo es 4 veces el área de ese rectángulo.
. Por tanto el área del círculo es 4 veces el área de ese rectángulo.
Y como podemos construir un cuadrado con área igual a un rectángulo dado (Elementos II.14), podemos cuadrar el círculo con regla y compás si nos dan el punto 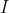 de la cuadratriz en el segmento
de la cuadratriz en el segmento  .
.
Demostración
A continuación damos la demostración que da Pappus de la propiedad  .
.
En  existe un punto
existe un punto 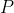 tal que
tal que  .
.
Con centro 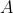 y radio
y radio  trazamos el arco de circunferencia
trazamos el arco de circunferencia  . Entonces
. Entonces  , porque las circunferencias son proporcionales a sus radios. Y como también
, porque las circunferencias son proporcionales a sus radios. Y como también  , tenemos que
, tenemos que  es igual al arco
es igual al arco  .
.
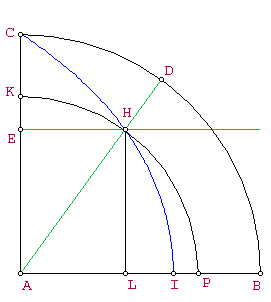

Supongamos que el arco  tiene un punto
tiene un punto distinto de
distinto de  en la cuadratriz (figura de la izquierda). Por definición de la cuadratriz:
en la cuadratriz (figura de la izquierda). Por definición de la cuadratriz:
Como  es igual a
es igual a  y
y  es igual a
es igual a  , resulta que
, resulta que  es igual a
es igual a  , lo que es absurdo. Por tanto
, lo que es absurdo. Por tanto
Supongamos ahora que la perpendicular a  por
por  tiene un punto
tiene un punto  distinto de
distinto de  en la cuadratriz (figura de la derecha).
en la cuadratriz (figura de la derecha).
Por definición de la cuadratriz,  . Como
. Como  es igual a
es igual a  y
y  es igual a
es igual a  , resulta que
, resulta que  es igual a
es igual a  , lo que es absurdo. Por tanto la perpendicular a
, lo que es absurdo. Por tanto la perpendicular a  por
por 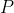 no tiene un punto en común con la cuadratriz, salvo quizá
no tiene un punto en común con la cuadratriz, salvo quizá 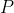 . Entonces
. Entonces  no puede ser menor que
no puede ser menor que  .
.
Pero hemos visto que tampoco puede ser mayor, luego el punto 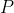 es el punto
es el punto 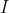 , y entonces
, y entonces  . como queríamos demostrar.
. como queríamos demostrar.
Obtener la ecuación de la cuadratriz en coordenadas polares y cartesianas no es difícil. A ver quién se atreve.
No hay comentarios:
Publicar un comentario