sábado, 27 de agosto de 2011

Formas diferenciales (conceptos básicos), homología y cohomología


Recientemente he tenido que escribir una pequeña introducción informal
 a la teoría de formas diferenciales. 


Aprovecho ese trabajo para extenderlo con explicaciones sobre cohomología
 y homología, que son conceptos que surgen de manera natural al tratar las formas diferenciales y su importancia. 

En este post hago uso libre de los conceptos topológicos que introduje en la entrada que hice sobre la conjetura de Poincaré.

 De hecho, esta entrada contiene material que usaré en el futuro cuando vuelva a hablar sobre la conjetura de Poincaré. 

En general el material de esta entrada es de uso ubicuo en física
 y matemáticas y posiblemente la use de referencia en el futuro 
en muy diversos temas.

Una forma diferencial puede ser entendida como un operador multilineal antisimétrico definido sobre un espacio vectorial. 

Dicho de otra forma sería un elemento del producto tensorial antisimetrizado de elementos del espacio dual a un vectorial.

 Para los propósitos de este post no es necesario dar los detalles algebraicos. 

Lo interesante es conectar esta definición algebraica con una definición operativa. 

Si consideramos que tenemos una familia de espacios vectoriales dependientes de unos parámetros continuos podemos tener una forma diferencial definida algebraicamente (a veces se usa el término “forma exterior” para referirse a la construcción algebraica reservándose el término “forma diferencial” para el caso general)) en cada punto.

 El caso mas sencillo es \mathbb {R}^n  considerado como espacio afín. 

Es decir, que en cada punto de \mathbb {R}^n  tenemos un espacio vectorial copia 
del espacio vectorial en el origen. 

De ese modo podemos tener una forma diferencial, en el sentido algebraico, en cada punto. 

Esto define una forma diferencial en \mathbb {R}^n  .

Una 0-forma sería simplemente una función. 

Si la forma pertenece al espacio dual será una 1-forma. 

Si pertenece al producto tensorial antisimetrizado
 de dos espacios duales sería una 2-forma, etc.

En \mathbb {R}^n  en la práctica esto redunda en una construcción bastante sencilla,
 como a que puede leerse en, por ejemplo, el libro de Marsden-Tromba 
de cálculo vectorial. 

Así una 1-forma es una expresión formal del estilo:

f=f_1(x_1,x_2,..., x_n)dx^1 + f_2(x_1,x_2,..., x_n)dx^2 + .....f_n(x_1,x_2,..., x_n)dx^n

dónde las f_i(x_1,x_2,..., x_n) son funciones arbitrarias de las coordenadas
 y las dxison una notación para indicar la base del espacio dual
 de la base canónica de \mathbb {R}^n

Una n- forma sería una expresión del estilo:

\omega=f_{ij...k}dx^i \wedge dx^j .... \wedge dx^k


En esta expresión se ha introducido un elemento nuevo, el producto exterior \wedge

 Este producto es una notación para el producto tensorial antisimetrizado . 

También puede definirse de otro modo, mediante unas propiedades sencillas:

Sea { dx_i } una base de un espacio vectorial V (o de su dual), que a su vez 
es un espacio vectorial). 

Un producto exterior, o producto cuña, de dos tales generadores se define exigiendo las reglas de cómputo (relaciones) siguientes:


1.dx_i \wedge dx_j = -dx_j \wedge dx_i \ si \ i \neq j

2. dx_i \wedge dx_i=0

Nota: Como estoy trabajando en \mathbb {R}^n  se tiene que la base dual y la base del espacio son isomorfas y que, además, las componentes covariantes y contravariantes de un tensor son las mismas.

A partir de esa propiedad de producto exterior de las bases puede, por linealidad, obtenerse el producto exterior de dos formas arbitrarias.

 En \mathbb {R}^3 , dado que el dual de \mathbb {R}^n  coincide con el mismo, puede identificarse
 una 1-forma con un campo vectorial. 

Y el producto exterior de dos 1-formas puede verificarse que coincide formalmente con el producto vectorial de dos vectores. 

Eso sí, el producto vectorial de una n-forma y una m-forma es una
 (n+m) forma. 

Por tanto el “producto vectorial” de dos 1-formas es una 2-forma, y, 
por tanto, un objeto diferente a los “vectores” de los que era producto. 

Sin embargo la identificación funciona porque una 1-forma arbitraria
 tiene 3 componentes y una 2-forma también
 (ya que los productos exteriores dx^i\wedge dx^i  se anulan) 

y al tener la misma dimensión, 3, pueden considerarse como “vectores” 
de dimensión 3.

El otro elemento importante de las formas diferenciales es la derivada exterior.

 Esta transforma un n-forma diferencial en una (n+1)-forma diferencial.

 La definición formal no es especialmente complicada. 

No obstante a efectos prácticos nos basta con la siguiente definición intuitiva:

d\omega= \sum_{i,j...,k,l} \frac{\partial f_{ij...k}}{\partial x^l} dx^l \wedge dx^i \wedge dx^j ... \wedge dx^k

Vamos a enlazar la derivada exterior con los elementos bien conocidos
 del cálculo vectorial. 

Si f es una 0-forma (recordemos, una función ordinaria) 
su derivada exterior es simplemente:

df=\sum_{i=1}^n \frac{\partial f}{\partial x^i} dx^i

Podemos, como antes, identificar esa 1-forma con un campo vectorial.

 De ese modo la derivada exterior de una 0-forma coincide con el gradiente
 de una función.

Para el caso de una 1-forma tenemos que su derivada exterior es:

d\omega = \sum_{i,j}\frac{\partial f_i}{\partial x^j} dx^j \wedge dx^i=\sum_{i<j}\left( \frac{\partial f_i}{\partial x^j} -\frac{\partial f_j}{\partial x^i}\right) dx^i \wedge dx^j

Si interpretamos la 1-forma como un campo vectorial y la 2-forma también como campo vectorial puede verse fácilmente que la derivada exterior coincide con el rotacional. 

Así mismo podría verse con sencillez que la derivada exterior de una 2-forma identificada a un campo vectorial nos daría la divergencia de ese campo. 

Nótese que la derivada de una 2-forma es una 3-forma. 

La 3-formas en \mathbb {R}^3  tienen una úrica componente no nula y,
 por consiguiente, pueden identificarse con funciones.

Hemos tratado n-formas en \mathbb {R}^n  . 

En una variedad arbitraria (una variedad es, informalmente hablando, 
la generalización a dimensiones arbitrarias de las curvas y superficies
 del analisis vectorial- o de la geometria diferencial clásica, 
si se prefiere verlo así-) tendríamos que en cada punto de la variedad
 va a estar definido su espacio tangente, que será un espacio vectorial.

 Este espacio a su vez tendrá su espacio dual. 

De ese modo podemos trasladar la maquinaria de las formas diferenciales
 en \mathbb {R}^n  a formas en variedades arbitrarias. 

La única circunstancia que da una complejidad extra es que tenemos
 mapas de la variedad a \mathbb {R}^n  y hay que lleva cuenta de esos mapas.

La derivada exterior permite introducir unos conceptos muy interesantes, 
muy útiles en topología diferencial.

i) Se dice que una forma es cerrada cuando su derivada exterior es 0. 

Este concepto es muy útil en física. 

En el caso en que se identifica una forma diferencial con un campo vectorial eso significaba que el rotacional era 0. 

Los campos con rotacional son campos conservativos.

 Eso significa que la integral de ese campo a lo largo de un camino
 cerrado es nula. 

O, equivalentemente, que la integral de dicho campo entre dos caminos distintos con el mismo origen y destino es independiente del camino. 

Como es bien sabido eso permite definir un potencial y el campo
 en cuestión es una derivada del potencial.

 Eso nos lleva al segundo concepto importante relacionado
 con la derivada exterior

ii) Se dice que una n-forma w diferencial es exacta cuando existe 
una (n-1)-forma diferencial f tal que w=df. 

Esto generaliza el concepto de potencial 
de un campo vectorial conservativo.

Puede verificarse usando la definición que toda forma diferencial exacta 
es cerrada, es decir, que d^2 w= 0 \ \forall w. 

Lo contrario es falso. 

Es decir, en general que una forma diferencial sea cerrada no significa
 que sea exacta. 

Se puede dotar a las formas diferenciales de grado n con una estructura 
de grupo siendo la operación de grupo la suma de formas diferenciales (definida de la forma obvia).

 El grupo cociente de las formas cerradas módulo las exactas se conoce
 como grupo de cohomología de de Rham definidas en una variedad diferencial M se denota como H^p(M,R). 

Enseguida comentaré algo sobre que es y que significa.

Antes un pequeña aclaración sobre como entender “módulo las exactas”.

 La idea es muy simple.

 En general el potencial escalar no está definido de manera única. 

Si tenemos que U(x,y,z) es un potencial para un campo vectorial \vec {V}(x,y,z) entonces U(x,y,z) + K (dónde Ka es una constante) también lo es. 

En electromagentismo tenemos el caso del potencial vector \vec{A}(x,y,z)
 de un campo magnético \vec{B}(x,y,z) que no está definido de manera única 
pues si a A le sumamos un campo con rotacional nulo nos dará el mismo campo magnético (recuérdese que el potencial vector cumple que su rotacional es el campo magnético. 

Obviamente sumar al potencial vector algo con rotacional nulo nos va a dar 
el mismo campo magnético). 

Esto se generaliza a formas diferenciales. Si f es tal que w=df se tiene que si a f le sumamos una forma cerrada g se va a seguir teniendo que w=dg.

 Es decir, que la forma diferencial que nos da w esta definida módulo 
formas cuya derivada sea nula.

En física las formas diferenciales se usan de manera muy libre 
con dx indicando “desplazamiento infinitesimal dx”. 

La teoría expuesta aquí formaliza ese concepto. 

Aparte de la relación entre el electroganetismo y las formas diferenciales hay muchas mas aplicaciones directas de esta teoría.

 Por ejemplo, en termodinámica las magnitudes termodinámicas como
 la energía, la entalpía o la energía libre de Gibbs son, formalmente, formas diferenciales.

 En relatividad general las variedades y las formas diferenciales 
son el lenguaje natural para expresar los conceptos.

 En teoría cuántica de campos y en teoría de cuerdas esta teoria de formas diferenciales, y la topologia algebraica y diferencial en general, 
juegan muy diversos papeles esenciales de las mismas.

Puede que a algún físico le haya extrañado la afirmación de que en general una forma diferencial cerrada no es exacta. 

Después de todo la condición de existencia de un potencial para un campo
 es que el rotacional sea nulo, osea, que la derivada exterior sea nula, 
y, por tanto, que la forma sea cerrada. 

La clave está en que normalmente se piensa en campos definidos en \mathbb {R}^n . 

Ahí si se cumple que una forma diferencial cerrada es exacta. 

Eso está conectado con el significado delos grupos de cohomología y,
 en particular, con el hecho de que los grupos de cohomologia
 de \mathbb {R}^n  sean triviales. 

En general en una variedad arbitraria M los grupos de cohomología serán distintos de 0.

 Puede demostrarse que si dos variedades son difeomorfas 
(es decir, existe un difeomorfismo entre ambas, lo que intuitivamente significa que una puede deformarse en otra de forma suave-entiéndase, diferenciable-) sus grupos de cohomologia de de Rham son isomorfos. 

El caso contrario es, en general falso. 

Dos variedades con los mismos grupos de cohomologia de de Rham
 no son difeomorfas.

El concepto de cohomologia expresado mediante formas diferenciales
 (la cohomologia de de Rham) es un caso particular de la definición general 
de cohomología. 

En general una cohomologia es el dual de una homología. 

La homologia es una de las primeras técnicas que se introdujo para intentar clasificar espacios que fueran homeomorfos (equivalentes topologicamente). 

La forma mas sencilla de homologia es la homología simplicial.

Un símplice es, hablando informalmente, algún tipo de conjunto geométrico sencillo cuyo significado tiene sentido en cualquier dimensión. 

Por ejemplo, podríamos definir los 0-símplices como conjuntos de puntos.

 Los 1-símplices como segmentos.

 Hasta ahí no hay arbitrariedad. 

Para definir un 2-simples ya si hay varias opciones.

 La más sencilla sería definir un 1-simplice como un triángulo
 (incluyendo su interior). 

Pero también podríamos definirlo como un rectángulo.

 Si optamos por la primera definición un 3-simples seria un prisma. 

Si optamos por la 2ª un 3 símplice sería un cubo. 

Por supuesto estas definiciones informales pueden y deben expresarse rigurosamente, pero para el propósito de esta entrada no es necesario.

El concepto de símplice nos lleva al concepto de complejo simpicial,
 que es, informalmente hablando, un conjunto de símplices unidos entre
 sí de manera adecuada.


(Imagen de un complejo simplicial)

Una vez dadas estas definiciones comentaré porque son útiles en topología.

 El concepto clave es que podemos hacer una correspondencia entre 
un complejo simplicial y un conjunto topológico. 

Podemos, por ejemplo, deformar (estirando sin romper) las caras 
de un tetraedro o un cubo para convertirlo en una esfera.

 Esto es lo que se conoce como una triangulación de la esfera 
(el nombre proviene del caso en que el símplice son las caras del tetraedro que son triángulos). 

En realidad un cuadrado puede verse como dos triángulos, así que está claro que no hay gran diferencia entre trabajar con símplices cúbicos o triangulares. 

En realidad cuando se habla de complejo simplicial se entiende tanto 
el símplice en sí como el conjunto topológico 
que se pone en correspondencia con él.

En el párrafo anterior he introducido subrepticiamente un concepto clave,
 el de frontera.

 Un símplice tiene una frontera, que a su vez es un conjunto de símplices (excepto los 0-símplices cuya frontera es nula). 

Un 1 simplex tiene como frontera dos puntos (dos 1-simplices). 

Un 2-simplice triangular tiene como frontera tres segmentos (dos símplices). 

Un tetraedro tiene como frontera 4 triángulos, etc.

Un conjunto simplicial es, como dije, un conjunto de símplices de la misma dimensión dispuestos de manera “adecuada”.

 En particular una de las condiciones de “adecuado” es que los símplices siempre estén unidos entre sí por fronteras.

 Esto permite definir para un conjunto simplicial arbitrario, 
que denotaremos por S, su frontera, que denotaremos por \partial S

 (Aquí el símbolo \partial significa frontera y no tiene nada que ver con
 su significado habitual en análisis de derivada parcial).

Nótese que, en general, la frontera de un complejo simplicial puede ser nula. 

Entender porque formalmente requiere dar una definición precisa del concepto de frontera de un complejo simplicial, en la que cada elemento de la frontera se le asigna un signo. 

Intuitivamente puede verse de una manera muy sencilla. 

Un complejo simplicial será cerrado cuando los símplices estén unidos entre
 sí de tal modo que tengan fronteras comunes de tal modo que las de unos símplices cancelan a las de otros.

 Un ejemplo muy intuitivo ilustra esta idea.

 Piensese en la esfera y su triangulación mediante un tetraedro. 

Cada tríangulo del tetraedro tiene vértices comunes con otro triángulo.

 Ese vértice común se cuenta con signo positivo para uno de los triángulos
 y con signo negativo para el otro de tal modo que en conjunto 
su contribución a la frontera es 0. 

Intuitivamente esto esta relacionado con el 
hecho de que la esfera es una superficie sin frontera.

Al igual que con las formas diferenciales formas aquí vamos a tener complejos simpiciales cerrados y exactos. 

Un complejo diferencial (también llamado cadena, a partir de aquí usaré
 este nombre) es cerrado cuando su frontera es nula. 

Una cadena es exacta cuando es la frontera de otra cadena.

Podemos definir formalmente la suma de cadenas (en realidad un complejo simplicial es la suma formal de símplices básicos)
 y se observa que con esa suma el conjunto de cadenas de dimensión n (obviamente las que están formadas por símplices de dimensión n) 
tiene estructura de grupo.

 Las cadenas exactas y las cerradas son subgrupos.

 Al igual que con las formas diferenciales puede verse que una forma exacta siempre es cerrada, pero que el converso es falso en general.

 Eso nos lleva a definir la homología simplicial como el grupo cociente entre cadenas cerradas módulo las exactas. 

El grupo de homologia (sobre un cuerpo K) de dimensión n de un complejo simpicial S se denota por H_n(S, k) .

Un aspecto muy importante a tener en cuenta en las aplicaciones es que en general para un espacio topológico podemos tener una cantidad arbitraria de triangulaciones. 

Lo importante es que los grupos de homología no dependen de la triangulación que elijamos.

Al igual que con la cohomología se tiene que dos espacios homemorfo tienen grupos de homología iguales, pero que, en general, puede haber espacios no homeomorfos con los mismos grupos de homología.

La cohomologia es el dual de la homología. 

Es decir, se trata de buscar una regla que asigne a cada cadena un número
 y que sea compatible con la estructura simplicial. 

En particular puede demostrarse que la cohomologia de de Rham
 es equivalente a la cohomologia singular en el cuerpo 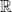\mathbb {R} .

 La cohomología singular es la cohomología “canónica” que se corresponde 
a la homología singular.

La homología singular depende en algunos tecnicismos de la simplicial,
 pero las ideas intuitivas de una y otra son las mismas.

La clave de la relación entre formas diferenciales y cohomologia es el concepto de integral de una forma en una variedad. 

Este generaliza al concepto de integral de línea y de superficie de un vector. 

Además si uno define el concepto e integral para variedades con frontera 
se obtiene el teorema de Stokes en variedaes, que generaliza los teoremas clásicos de Stokes, de Green y de Gauss del análisis vectorial. 

Para dar definiciones adecuadas de estas integrales tendría que dar muchas nociones de teoría de variedades y eso requeriría escribir al menos tanto como lo que ya he escrito y por consiguiente, lo dejaré para otra ocasión. 

No obstante puede entenderse intuitivamente la idea. 

A un símplice le corresponde un trozo de una variedad.

 Uno puede integrar una forma diferencial en ese trozo para 
obtener un número. 

Eso respeta las estructuras homológicas necesarias y puede verse 
que define una cocadena. 

El grupo de cocadenas os da el grupo de cohomología, 
y este es equivalente al grupo de cohomologia de de Rham.

La clave de la homología y la cohomologia desde el punto de vista matemático es que los grupos homologicos y cohomlógicos son relativamente sencillos de calcular (en particular más sencillos que los grupos de homotopía). 

En física es mas normal trabajar con cohomología y formas diferenciales pues las cantidades físicas más habituales son muchas veces, en el fondo, 
formas diferenciales.
Publicado por en

No hay comentarios:

Publicar un comentario