¿Qué es una línea recta?
Las líneas rectas se identifican por esta fórmula  ,
,
donde m es la pendiente de la recta y n la ordenada en el origen (donde corta con el eje Y) (nos estamos restringiendo a rectas en el plano XY.
Si la línea recta no tiene pendiente m=0, tenemos que toma la forma
y = n es decir, una línea horizontal que corta al eje Y en el valor n.
¿Las curvas tienen pendiente?
Efectivamente, las líneas curvas tienen pendiente y para identificarla
¿qué hemos de hacer?
Pues muy fácil, nos ponemos en el punto que queramos calcular la pendiente de la línea curva, y buscamos la recta tangente a ese punto.
La pendiente de dicha recta es justamente la pendiente de esa curva en ese punto. Obviamente las líneas curvas tendrán una pendiente distinta en cada punto.
¿DERIVADAS?
Las derivadas son una forma de ver como cambia una función, una curva, en términos de su variable.
Antes hemos puesto y=mx+n (queremos ver cómo cambia y cuando cambiamos x). Bien, estudiemos ese caso:
A la variación en y (que claramente depende de x, con lo cual podemos escribir y(x) o f(x)=mx+n) la llamaremos dy.
A la variación de x la llamaremos, dx.
Para ver como cambia y (dy) cuando cambia x (dx), simplemente hemos de calcular 
¿Y ESO CÓMO SE CALCULA?
Eso es una derivada y para nosotros será suficiente en esta entrada aprender como se calculan derivadas de funciones , curvas, que dependen de potencias de x,  y números.
y números.
La regla es fácil bajamos el exponente a la x y la elevamos al antiguo exponente menos 1:
Ejemplo:
Si  , la derivada
, la derivada 
Poniendo numeritos:
Si  , la derivada
, la derivada 
Si  , la derivada
, la derivada 
Por otro lado, si y=n su derivada es nula, es lo lógico, por mucho que cambie la x la y siempre es n, nunca cambia, por tanto su derivada es cero.
Otro detalle, si y=mx^n, las reglas de las derivadas dicen que los números salen de la derivada:
Poniendo numeritos:
Ultimo apunte, si tenemos 
Es decir, que si tenemos una función que se puede ver como suma de dos funciones (o resta), la derivada de dicha función es la suma de derivadas.
Por qué la pendiente se relaciona con la derivada.
Tomemos una recta y=mx+n y calculemos la derivada:
así que efectivamente la derivada te da la pendiente de la recta.
MÁXIMOS Y MÍNIMOS:
¿Cómo sabemos que una curva tiene un máximo o un mínimo?
Fácil, vamos estudiando las pendientes de las rectas tangentes a la curva.
Si tengo un máximo está claro que, independientemente de cómo me mueva en la curva de derecha a izquierda o de izquierda a derecha, las pendientes de las curvas tienen primero que crecer y luego tienen que decrecer.
Pero para pasar de crecer a decrecer, en algún momento se tiene que hacer cero.
Pues justamente en el punto en el que se hace cero la curva tiene un mínimo.
Análogamente, si tengo un mínimo está claro que las pendientes de las curvas tienen primero que decrecer y luego tienen que crecer.
Pero para pasar de decrecer a crecer, en algún momento la pendiente también tiene que hacerse cero.
Pues justamente en el punto en el que se hace cero la curva tiene un mínimo.
Es decir que pendiente de la recta tangente igual a cero implica que es un máximo o un mínimo (para decidir si es máx o mín hay que ver si la curva es tal que las pendientes primero crecen y luego decrecen o viceversa y para eso hay que recurrir a la segunda derivada, pero esa es otra historia).
Para lo que nos ocupa esto es suficiente porque conoceremos la forma de la curva que nos interese en esta entrada y podremos ver si es máx o mín.
Hagamos tres ejemplos
Ejemplo 1
Esto es una parábola (sólo tiene un mínimo).
Entonces calculamos la pendiente de las rectas tangentes, es decir, la derivada
Ahora nos preguntamos cuando se hace cero: 
Y resolvemos esta ecuación:  .
.
Y si queremos saber el punto, necesitamos tanto x como y.
Así que sustituimos este valor en la función y obtenemos: y=5.
Así que la parábola tiene un mín en (0,5).
Ejemplo 2
Pongamos esta función: 
Calculamos su derivada: 
La igualamos a cero: 
Resolvemos:
Observamos que tenemos tres soluciones, pero dos de ellas son complejas y nosotros estamos trabajando con una función real y representable en el plano real, por lo tanto el único punto donde pude haber un máx o mín es en el de x=0.
Ejemplo 3
Pongamos esta función: 
Calculamos su derivada 
La igualamos a cero: 
Resolvemos:
Por lo tanto, tenemos una máx para x=0 y dos mín uno para  y otro para
y otro para  .
.
El mecanismo de Higgs:
Como sabemos de la escuela para cada campo tenemos un potencial asociado.
Para el campo gravitatorio producido por una masa m tenemos que su potencial es:
Donde tenemos un coeficiente Gm que esencialmente es la masa
(La constante se puede redefinir para que valga 1)
Para el campo eléctrico producido por una carga q tenemos que su potencial es:
Aquí tenemos un coeficiente Kq que básicamente es la carga,
(la constante se puede redefinir para que valga 1)
Ahora introduzcamos el campo de Higgs, así que elegimos esta letra  .
.
El potencial del campo de Higgs, que se deriva de una concienzuda teoría cuántica de campos, tiene esta forma:
donde 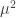 y
y  son números positivos.
son números positivos.
Comparemos esto con  … Sí, es exactamente lo mismo simplemente usando otras letras.
… Sí, es exactamente lo mismo simplemente usando otras letras.
Ahora podríamos sacar los max y mín del potencial de Higgs y tendríamos que calcular las derivadas  , el resto es igual, que el caso que hemos hecho.
, el resto es igual, que el caso que hemos hecho.
Es decir aquí la Y es la energía potencial y la X son los valores del campo.
Así tenemos que el campo de Higgs tiene un max en 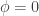 y dos mín en
y dos mín en
Rotura de simetría:
Pongamonos en situación, somos el campo de Higgs, y estamos en 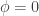 .
.
En la cima de la montaña, y entonces vemos que todo es simétrico, a un lado y al otro.
Pero hay un problema, 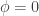 significa que no hay campo, el campo de Higgs es 0, pero resulta que su energía potencial no lo es.
significa que no hay campo, el campo de Higgs es 0, pero resulta que su energía potencial no lo es.
Cosa rara, tenemos un campo que vale cero, pero su energía no es cero. Y qué significa que el campo es cero.
Pues como ya habrán oído o leído por ahí en cada campo cuántico encontramos que sus excitaciones se comportan como partículas, y las partículas del campo de Higgs es el famoso, famosísimo bosón de Higgs, así que campo 0 implica que no hay partículas de Higgs por ningún sitio.
Pero es que si no tiene partículas, ocurre que la energía del campo es diferente de cero.
Y sabemos que tenemos dos mín, dos sitios con energía nula (o en todo caso menor que la del máx) pero ojo, el campo ahí ya no vale cero, entonces hay partículas de Higgs.
Pero resulta que los sistemas decaen a estados energéticos menores, y así lo hace el campo de Higgs, y pufff, de repente encontramos partículas de Higgs por ahí rondando.
Y encima entendemos que tienen que tener una masa ( ) y ahí andamos buscandolos.
) y ahí andamos buscandolos.
Así que el campo pasa espontáneamente de 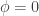 a una de las otras dos opciones
a una de las otras dos opciones
,a o a
o a  .
.
Entonces ahora se encuentra en el “valle” y ya no hay simetría a su alrededor.
Por eso a este fenómeno se le llama rotura espontánea de la simetría.
Lo genial de todo esto es que si esto ocurre así, hay un hecho indirecto muy interesante.
Resulta que si uno estudia la interacción electromagnética y la débil en la teoría cuántica, esas interacciones llevan asociadas cuatro partículas, el fotón 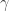 para el electromagnetismo y los bosones Z y
para el electromagnetismo y los bosones Z y  y
y  .
.
Resulta que todos esos bosones son a primeras luces idénticos, por eso se pueden unificar las interacciones electromagnética y débil en la teoría electrodébil.
Sin embargo los bosones débiles tienen masa (de hecho bastante grande) y el fotón no.
Pues lo curioso es que esta “rotura espontánea de la simetría” tiene como efecto dar masa a los bosones Z y W pero no al fotón. Justamente lo que vemos.
Este es el mecanismo más conocido y mejor estudiado de dotar masa a las partículas.
Pero hay otros que no necesitan del Higgs,
algún día lo mismo contamos alguno.



No hay comentarios:
Publicar un comentario