miércoles, 22 de mayo de 2013

Café matemático: Los teoremas de convergencia

Esta entrada comprende tres teoremas que se encuentran entre los más importantes del Análisis Matemático. La potencia y la utilidad de estos teoremas constituyen la principal ventaja teórica de la integral de Lebesgue sobre la integral de Riemann.
Teorema 
(Teorema de la convergencia monótona). Sea 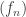(f_n) una sucesión no decreciente de funciones medibles no negativas y sea \displaystyle{f(x)= \lim_{n \rightarrow \infty} f_n(x).} Entonces se tiene
\displaystyle{\int f = \lim_{n \rightarrow \infty} \int f_n.}
Corolario
 (Teorema de Beppo Levi). Si 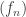(f_n) es una sucesión de funciones medibles no negativas entonces se tiene
\displaystyle{\int\sum_{n=1}^\infty f_n = \sum_{n=1}^\infty \int f_n.}
Teorema
 (Lema de Fatou). Si 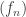(f_n) es una sucesión de funciones medibles y no negativas entonces se tiene
\displaystyle{\int \liminf_{n \rightarrow \infty} f_n \leq \liminf_{n \rightarrow \infty} \int f_n.}
Teorema 
(Teorema de la convergencia dominada). Sea 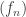(f_n) una sucesión de funciones medibles que converge puntualmente hacia cierta función f y supongamos que existe una función integrable g tal que |f_n(x)| \leq g(x). Entonces se tiene
\displaystyle{ \int f = \lim_{n \rightarrow \infty} \int f_n.}
Publicado por en