lunes, 27 de mayo de 2013

Café matemático... Un conjunto no medible


Vamos a demostrar la existencia de un conjunto no medible.
 Se define una relación de equivalencia en el intervalo [0,1) del siguiente modo: dos números x,y \in [0,1) son equivalentes si x-y \in \mathbb{Q}. 
Esta relación define una partición del intervalo [0,1) en clases de equivalencia.
 Gracias al axioma de elección, existe un conjunto S \subseteq [0,1) que contiene exactamente un elemento de cada clase.
 Sea ahora (r_j) una numeración de los números racionales en el intervalo (-1,1) y sea 
S_j=r_j+S. 
Veamos cómo (S_j) es una sucesión de conjuntos disjuntos. 
Si x \in S_j \cap S_k entonces x=r_j+s_j y x=r_k+s_k con s_j,s_k \in S, 
pero s_j-s_k=r_k-r_j \in \mathbb{Q}, luego s_j=s_k y por lo tanto j=k. 
Además se tiene
\displaystyle{[0,1) \subseteq \bigcup_{j=1}^\infty S_j \subseteq (-1,2),}
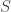porque si x \in [0,1) entonces x está en alguna clase de equivalencia, luego existe algún y \in S tal que x-y \in \mathbb{Q}, de modo que x-y=r_j para algún j \geq 1, y así x \in S_j.Ahora probamos que S no es medible por reducción al absurdo. 
Si 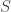S es medible entonces S_j es un conjunto medible con m(S_j)=m(S) para todo j \geq 1 y por lo tanto
\displaystyle{m ( \bigcup_{j=1}^\infty S_j) = \sum_{j=1}^\infty m(S_j)= \sum_{j=1}^\infty m(S),}
y esto es una contradicción porque \displaystyle{ 1 \leq m (\bigcup_{j=1}^\infty S_j) \leq 3}, mientras que la serie \displaystyle{ \sum_{j=1}^\infty m(S)}converge a cero o diverge, según sea la medida m(S) nula o positiva.
Publicado por en