Voy a dar un bosquejo del razonamiento.
La idea es sencilla, los neutrinos viajan en un “universo menguante” debido a que la masa de la tierra contrae el universo en sus inmediaciones.
Esto puede parecer chocante si uno piensa en el campo gravitatorio terrestre en términos de una métrica de Scharschild.
Según el efecto del campo gravitatorio hace cosas como alterar la velocidad de los relojes, de relevancia en el GPS, desviar ligeramente la trayectoria de los neutrinos respecto a la línea recta, en cantidades absolutamente despreciables y cosas así.
El truco está en ver las cosas desde el punto de vista de los neutrinos.
Estos avanzan por un medio material que , más o menos, en las inmediaciones de la trayectoria, es homogéneo e isótropo.
Esas dos palabras automáticamente remiten a una métrica FRW y a modelos cosmológicos.
El lector sin conocimientos previos de cosmología, per que sepa relatividad general, puede visitar la entrada de wikipedia sobre el tema: Friedmann–Lemaître–Robertson–Walker metric.
Para usar el formalismo FRW al presente caso debemos revisar algunos conceptos y adaptarlos.
Lo primero es admitir que podemos aproximar el espacio local de los neutrinos
por un universo uniforme e isótropo.
Si asumimos que la tierra que atraviesan tiene variaciones mínimas de densidad esto es así.
El campo gravitatorio radial correspondiente a una métrica de Schwarschilld (o el análogo con materia, la solución de Tollman-Oppenhemier) son irrelevantes ya que, como argumenté, no desvían a los neutrinos de una trayectoria recta.
Entonce tenemos las ecuaciones de FRW:


Estas son unas ecuaciones diferenciales ordinarias para componentes de una métrica.
El factor a es el “radio 4 dimensional”, rho es la densidad del medio, ka es la curvatura del universo y Sigma la constante cosmológica.
El significado del resto de términos viene explicado en la wiki y menciono estos porque son los que necesito reinterpretar.
Para empezar tenemos que tratar a, el radio 4 dimensional, y como pensar en un universo en expansión
(o contracción) adaptado a nuestro caso.
La idea de la cosmología es que el universo se está expandiendo como si fuese
una esfera en 4-dimensiones de radio a.
Obviamente el interior de la tierra no es un universo y no vamos a tener que pensar en términos locales.
La clave es fijarse en un factor local, el ritmo de expansión del universo, es decir  .
.
También podemos olvidarnos de la curvatura ya que en el trayecto tan corto que cubren los neutrinos no juega ningún papel, y, por el mismo motivo, de la constante cosmológica.
Eso nos deja con que:
1. 
En cosmología la densidad es la masa partida por el volumen, y por tanto, dado que el volumen varía la densidad también lo hace.
Por eso las ecuaciones de FRW son un sistema de dos ecuaciones diferenciales.
En nuestro caso las cosas cambian. Dado que la densidad crítica del universo es mucho menor que la densidad de la tierra podemos asumir sin problemas que, localmente, el universo se está contrayendo (aunque globalmente se este expandiendo).
Eso haría que la tierra disminuyese de tamaño si la materia de la tierra fuese como la que se considera en cosmologia, un fluido, posiblemente con presión.
Pero la tierra es sólida y mantiene su forma incluso aunque el universo este encogiendo.
Aún así, para simplificar, yo asumo que la idea del tensor energía momento del fluido nos vale. Simplemente asumo que no tengo que preocuparme de la presión y el único factor a tener
en cuenta es la densidad.
He buscado algo sobre tensores energía momento relativistas de medios continuos, pero no he hallado nada, así que confío en que mi simplificación valga.
En última instancia la idea es buscar algo razonable que nos permita hacer cálculos.
Si los resultados salen erróneos nos olvidamos, y si salen más o menos bien ya los analizamos a fondo.
Bien, entonces basta sustituir en la ecuación 1 los valores.
Nos da para  un valor de 5.5437 x 10^-5.
un valor de 5.5437 x 10^-5.
Esto es, superficialmente, interesante ya que el factor de violación de la velocidad de la luz de los neutrinos(v-c)/c también es del mismo orden, en concreto es 2.48x 10^-5.
Si ambas cantidades fuesen adimensionales esta coincidencia sería mas significativa, pero no es el caso. Aun así no estamos muy lejos.
Si usamos infnitésimos tenemos que  .
.
Vamos a usar esta aproximación de infinitésimos para ver como precisar la comparación.
Recordemos que los neutrinos recorren un trayecto, d=731.278 metros.
Si fuesen a la velocidad de la luz tardarían un tiempo t=d/c en recorrer ese trayecto.
Ese t es el que va a jugar el papel de 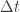 .
.
A la diferencia entre el tiempo que tarda la luz en recorrer el trayecto y la que tardan los neutrinos la denomino  .
.
Ahora voy a hacer otra simplificación.
Voy a considerar que los neutrinos no recorren el total de los kilómetros vistos desde el exterior (los que mide el GPS) sino que como el universo se está encogiendo en realidad recorren una distancia menor, que es la distancia inicial entre ambos puntos, menos la cantidad que se ha encogido el universo.
Este es un punto sutil ya que en realidad, aunque el universo se está encogiendo la tierra no lo hace y los puntos, por fuera, siguen a la misma distancia.
El caso es similar al “Warp drive” de alcubieere: Alcubierre drive.
La idea de warp drive es la siguiente.
Quiero ir del punto a al b, separados por una distancia, en métrica plana, d.
Y quiero ir “mas rápido que la luz”, pero sin violar la relatividad.
El truco es hacer que la métrica delante de nosotros “encoja” y detrás “se estire”, de tal forma que, en todo momento, la distancia total siga siendo d.
Si hacemos eso nosotros nos vamos siempre moviendo a una velocidad inferior a c, pero tenemos que recorrer, en nuestra métrica local, una distancia d’
Aquí no voy a usar todos los detalles del modelo Alcubierre (con su correspondiente adaptación)
y me voy a limitar a una aproximación muy grosera.
Simplemente me voy a preocupar si el resultado de recorrer la distancia original "encogida" por nuestro universo menguante nos da un orden de magnitud adecuado.
Sustituyendo en las expresiones anteriores tengo:
Si se hacen las cuentas (y no me he equivocado en algún lado, y no me he saltado ninguna constante de esas que los autores- en concreto Collins, Martins y Squires cuyo libro "particle physics and cosmology"
he usado de referencia- gustan de hacer iguales a 1 sin avisar)
el resultado para el diferencial de tiempos es a.4.504 x10^-16.
Ahora viene un punto sobre el que aún no tengo clara la interpretación que debo dar.
Este a es el radio del universo y, obviamente, quiero trabajar a nivel local y no debería aparecer.
Debería estar todo en términos del cociente  , pero no es el caso (ver P.S. 2).
, pero no es el caso (ver P.S. 2).
Si, así a lo bruto, sustituyo a por la distancia resulta un valor para el incremento del tiempo
de 3.24 x10 ^-11 sgs= 3.24^10-2 ns.
Teniendo en cuenta que el resultado experimental para ese tiempo es de 60.7 ns estoy tres órdenes de magnitud fuera del valor observado.
Dada la cantidad de simplificaciones brutales, y el error conceptual pendiente de como interpretar a (o como librarme de él) creo que es un fallo corregible si se hacen las cosas con más cuidado.
Más importante, creo que la idea en si misma es conceptualmente elegante.
Básicamente estoy teniendo en cuenta algo que la RG nos dice que debe ocurrir (que el universo encoja) y viendo si ese ritmo de encogimiento, irrelevante para casi cualquier otro propósito, tiene un orden de magnitud medianamente similar a lo que observamos.
Y, pese a la brutalidad de las aproximaciones, y a que hay algún detalle conceptual no muy claro,
resulta que es así.
Si estuviese en una cátedra no presentaría los cálculos en una fase de concepción
tan pedreste cómo lo he hecho aquí.
Pero, claro, si me pagasen habría tenido mucho mas tiempo, y motivación, para ponerme con las cuentas y hacerlas con toda propiedad, y las habría tenido listas hace semanas.
Siendo como son las cosas queda así tal cuál.
Si a alguien le apetece comentar, indicando errores, criticando la aproximación (para bien o para mal) y, incluso, si le apetece usar esta base y hacer bien las cuentas y si haciéndolo bien salen los valores del experimento y publica un artículo que le de fama, por mi no hay problema,
tanto si me menciona en las referencias como si no.
A mi lo que me interesa es ver si esta idea resuelve el problema planteado y no me importa demasiado si los detalles los hago yo o los termina otra persona por mí.
Obviamente, asumo que lo mas probable es que este totalmente equivocado y que algún investigador profesional dará con la respuesta correcta.
Aún así, aún así, tal vez tenga razón, y o bien yo mismo, u otra persona, rehará bien las cuentas
y se explique el resultado, soñar es gratis .
Meditando sobre el asunto creo que dado que el ritmo de expansión del universo en un modelos cosmológico depende del radio del mismo en un momento dado en realidad si deben depender los resultados de a, y no sólo del cociente.
Si admito eso debería buscarse alguna propuesta “natural” en algún sentido para ese valor
(que, obviamente no es el radio cosmológico), ni tampoco creo que deba ser el valor de la distancia entre
el CERN y el observatorio.
En principio, según se me ocurre ahora, debería ser algún tipo de magnitud relacionada con alguna distancia respecto al centro de la tierra a partir de la cuál debamos olvidar esta aproximación
y volver al ritmo general de expansión del universo.
Obviamente mientras este valor de A tenga un valor arbitrario puede elegirse cualquier valor del mismo,
en particular el que sirve para obtener el valor exacto del experimento.
Lógicamente eso hace que la teoría no tenga ningún valor predictivo hasta que no se resuelve este asunto. Intuitivamente pienso que si el radio debemos fijarlo por algún tipo de condición de contorno respecto al punto en cuál el universo recupera su comportamiento promedio tal vez podría ser razonable un valor en un rango de valores próximo al que se necesitaría para obtener el resultado experimental, pero puede que eso sea “whisiful thinking”, o “buenos deseos”.