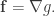Se dice que un campo vectorial  de clase
de clase 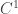 en un abierto
en un abierto  es cerrado si se verifican las condiciones
es cerrado si se verifican las condiciones
Supongamos que  es conservativo, es decir, que existe un campo escalar
es conservativo, es decir, que existe un campo escalar  de clase
de clase 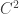 tal que
tal que 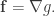
Tenemos como consecuencia de la igualdad de las derivadas parciales cruzadas que
y por lo tanto el campo  es cerrado.
es cerrado.
El lema de Poincaré afirma que el recíproco es cierto si la geometría del dominio es favorable.
Lema de Poincaré.
Sea  un campo vectorial de clase
un campo vectorial de clase 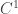 en un abierto convexo
en un abierto convexo 
Si  es cerrado entonces
es cerrado entonces  es conservativo.
es conservativo.
Demostración.
Se puede suponer sin pérdida de generalidad que 
Sea  el campo escalar definido mediante la expresión
el campo escalar definido mediante la expresión
Calculando las derivadas parciales de  resulta
resulta
La función 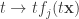 es una primitiva del integrando, puesto que
es una primitiva del integrando, puesto que
Se sigue de la regla de Barrow que
de donde se deduce que