La segunda ley de la termodinámica afirma que en un sistema aislado la entropía nunca decrece. El demonio de Maxwell (1867) logra violar esta ley actuando directamente sobre los grados de libertad microscópicos del sistema. Szilard demostró que un demonio de Maxwell clásico puede extraer de un ciclo termodinámico como mucho un trabajo igual a k T log(2), donde k es la constante de Boltzmann y T es la temperatura.
Físicos japoneses han demostrado que un demonio de Maxwell cuántico puede extraer hasta el doble, 2 k T log(2), gracias al uso del entrelazamiento cuántico; este valor corresponde a la diferencia entre la información cuántica mutua entre el demonio y el sistema realimentado de control necesario para controlar sus acciones. En este sentido, este trabajo se puede interpretar como la conversión de información en energía.
El campo de la termodinámica de la información cuántica promete sorpresas experimentales muy interesantes en los próximos años. Nos lo cuenta KFC, “Entangled Particles Break Classical Law of Thermodynamics, Say Physicists. Japanese physicists show how to extract more energy from entangled particles than is possible with classical thermodynamics,” The Physics ArXiv Blog, August 1, 2012, haciéndose eco del artículo técnico de Ken Funo, Yu Watanabe, Masahito Ueda, “Thermodynamic Work Gain from Entanglement,” arXiv:1207.6872, Subm. 30 Jul 2012.
La figura que abre esta entrada muestra el protocolo de transferencia de entropía que utiliza el demonio de Maxwell cuántico. La parte (a) muestra que los subsistemas A y B están inicialmente entrelazados y hay una entropía negativa debido a la correlación entre ambos subsistemas igual a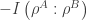 
.
.
La entropía de los subsistemas A y B se puede reducir una cantidad 
si se realiza una transformación unitaria del estado total. La parte (b) muestra que al realizar una medida del subsistema A se produce una transferencia de entropía del sistema hacia una memoria M. La correlación cuántica entre el sistema AB y la memoria M implica una ganancia de entropía igual a 
, que se compensa con la entropía positiva que gana la memoria M, igual a 
. La parte (c) muestra el sistema realimentado de control, cuyo papel es clave en el protocolo. Este sistema de control actúa sobre los subsistemas A y B, produciendo una entropía negativa 
y 
, cuyo origen es la correlación inicial y la ganancia debida a la información .
si se realiza una transformación unitaria del estado total. La parte (b) muestra que al realizar una medida del subsistema A se produce una transferencia de entropía del sistema hacia una memoria M. La correlación cuántica entre el sistema AB y la memoria M implica una ganancia de entropía igual a , que se compensa con la entropía positiva que gana la memoria M, igual a . La parte (c) muestra el sistema realimentado de control, cuyo papel es clave en el protocolo. Este sistema de control actúa sobre los subsistemas A y B, produciendo una entropía negativa 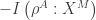y , cuyo origen es la correlación inicial 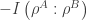y la ganancia debida a la información .
Como consecuencia, la entropía total de los subsistemas A y B disminuye y se puede extraer trabajo útil de ellos. La correlación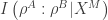 
entre los subsistemas A y B, aunque no nula, no puede ser utilizada para extraer trabajo (al menos que se realice otra transformación unitaria en el sistema total).
entre los subsistemas A y B, aunque no nula, no puede ser utilizada para extraer trabajo (al menos que se realice otra transformación unitaria en el sistema total).
Como esta explicación es muy técnica, requiere un comentario para legos (que obviamente incluirá “licencias poéticas” que los japoneses no han podido demostrar en su artículo).
El demonio de Maxwell clásico actúa de la siguiente forma. Imagina dos cajas llenas de sendos gases a la misma temperatura. Entre ambas cajas se encuentra una trampilla bajo el control del demonio. El demonio deja pasar las moléculas lentas que se acercan a la trampilla desde la caja izquierda a la derecha, e impide que las moléculas lentas de la derecha salgan de ella. Además, el demonio deja pasar las moléculas rápidas que se acercan a la trampilla desde la caja derecha a la izquierda, e impide que las moléculas rápidas de la izquierda salgan de ella. Como resultado de la acción el demonio, la caja izquierda se calienta (la velocidad promedio de sus moléculas crece) y la caja derecha se enfría.
Este gradiente de temperatura nos permite extraer trabajo útil del sistema.
En el protocolo de acción del demonio cuántico se supone que las partículas de ambas cajas están entrelazadas, de tal forma que la acción del demonio sobre una de ellas implica la acción sobre la otra (es decir, al dejar pasar una partícula rápida de la caja derecha a la izquierda, también se está dejando pasar una lenta de la izquierda a la derecha).
Por ello, la acción del demonio conduce a la producción del doble de trabajo en el caso cuántico que en el clásico.
