domingo, 25 de agosto de 2013

Bienvenidos al Caos (30077)


Todos hemos oído hablar de la teoría del caos. 
No se puede negar que el nombre es sugerente. Entre mariposas que crean tormentas y la impotencia a la hora de hacer predicciones, pocas veces se pone uno a toquetear el caos de verdad.
En esta entrada vamos a intentar jugar con el caos con el ejemplo más simple en el que podemos encontrarlo.
 Les voy a presentar la aplicación logística, y vamos a manipularla para sacar de ella muchas cosas interesantes.
Advertencia:
 Sería genial que tuvieran una calculadora a mano ;) (da igual que sea de primera o de última generación).
El ingrediente principal: La aplicación logística
Esta aplicación no es más que una función iterativa.
 ¿Qué significa eso de ‘iterativa’? 
 Pues que introducimos un valor elegido para la incógnita  hacemos las operaciones que nos diga la función, obtenemos un resultado, y ese resultado lo volvemos a meter en la incógnita  volvemos a operar y obtenemos un nuevo resultado. Este proceso lo podemos repetir tantas veces como queramos.
 A cada paso de este procedimiento lo llamaremos, iteración.
La aplicación de marras, la logística, tiene esta forma:
x_{n+1}=rx_n(1-x_n)
  1. x_n Es la incógnita obtenida en el paso n de la iteración.
  2. n nos indica el número de la iteración y toma valores 0, 1, 2,..
  3. r es un valor real, puede tomar cualquier valor real positivo. Este coeficiente nos servirá para modular distintos comportamientos de la aplicación como veremos.
  4. x_{n+1} es la solución obtenida al introducir el valor x_n de la iteración previa.
Un ejemplo:
Elegimos 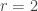r=2.
Elegimos el valor inicial de la variable, 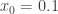x_0=0.1
Comenzamos:
  1. n=1.  x_1=2\times 0.1(1-0.1)=0.18
  2. n=2. Introducimos el valor anterior x_2=2\times 0.18(1-0.18)=0.2952
  3. Repetimos el proceso
Veamos algunos casos:
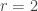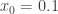
Para r=2, x_0=0.1
x_0=0.1000000000
x_1=0.1800000000
x_2=0.2952000000
x_3=0.4161139200
x_4=0.4859262512
x_5=0.4996038592
x_6=0.4999996861
x_7=0.5000000000
x_8=0.5000000000
x_9=0.5000000000
x_{10}=0.5000000000
Esto lo podemos ver de forma gráfica. Disponemos en el eje vertical los valores de 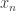x_n y en el eje horizonta n (el orden de la iteración). 
Así en este caso podemos ver que el sistema se estabiliza para el valor 0.5.
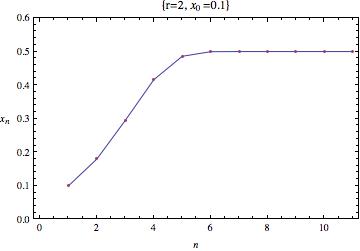
recursividad1
Aprovecharemos este método gráfico para ver más claramente lo que pasa cuando jugamos con el factor r.
Para r=2.5 y x_0=0.1:
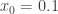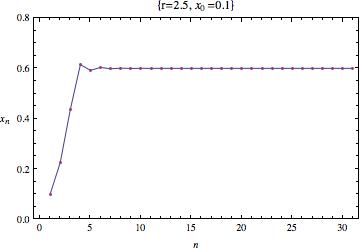
recursividad2
En este caso vemos como el sistema se estabiliza para el valor o.6.
 También es interesante observar que se llega a este punto estable en un número de iteraciones más alto.
Para 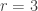r=3 y x_0=0.1
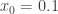
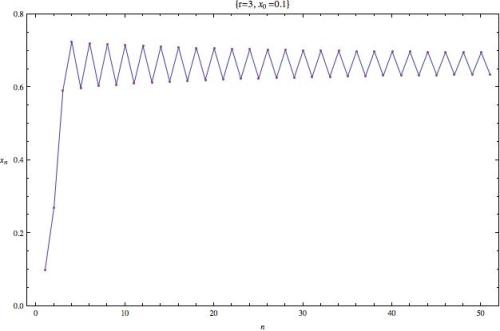
recursividad3
Aquí surge una cuestión interesante, ahora tenemos que el sistema oscila entre dos valores, 0.643 y 0.688.  
El sistema pasa de tender a un punto estable a tener una oscilación entre dos valores. A cada paso en la oscilación salta entre uno de esos dos valores.
Para r=3.2 y x_0=0.1
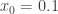
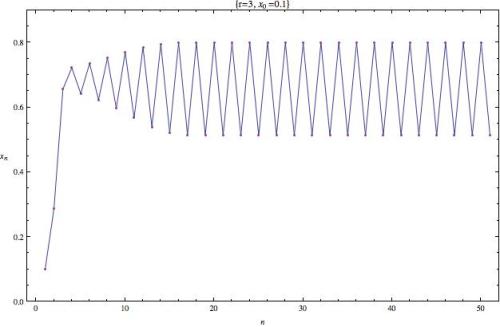
recursividad4
El comportamiento se mantiene, estamos oscilando entre dos valores.
 En cierto sentido, hemos doblado el periodo, ahora en vez de caer en el mismo valor cada salto (iteración), tenemos que esperar dos saltos para llegar al mismo valor.
Pero la historia no acaba aquí, sigamos.
Para 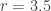r=3.5 y x_0=0.1:
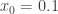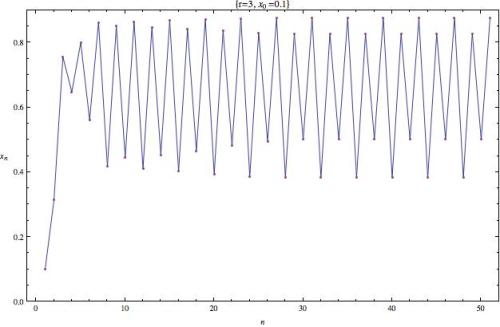
recursividad5
Aquí el sistema pasa a oscilar entre 4 puntos diferentes, se queda saltando entre cuatro valores. Se puede decir que hemos vuelto a doblar el periodo.

Si vamos aumentando la r los periodos se irán duplicando y cada vez con mayor rapidez al aumentar el parámetro.  
Al final llegamos un punto en el que el periodo es infinito, es decir, nunca volvemos a un valor previo, ¡hemos llegado al caos!. 
Para r=4 y x_0=0.1:
recursividad6

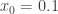Bifurcación, el periodo se dobla


Los matemáticos se pusieron a estudiar esto como locos y miraron los puntos estables que se tenían en la aplicación logística cuando se va aumentando el valor del parámetro. 
 Lo que descubrieron es justamente lo que nosotros hemos visto aquí, que el periodo se va doblando en valores concretos del parámetro hasta que llega un momento en el que el periodo es infinito y se llega al caos:
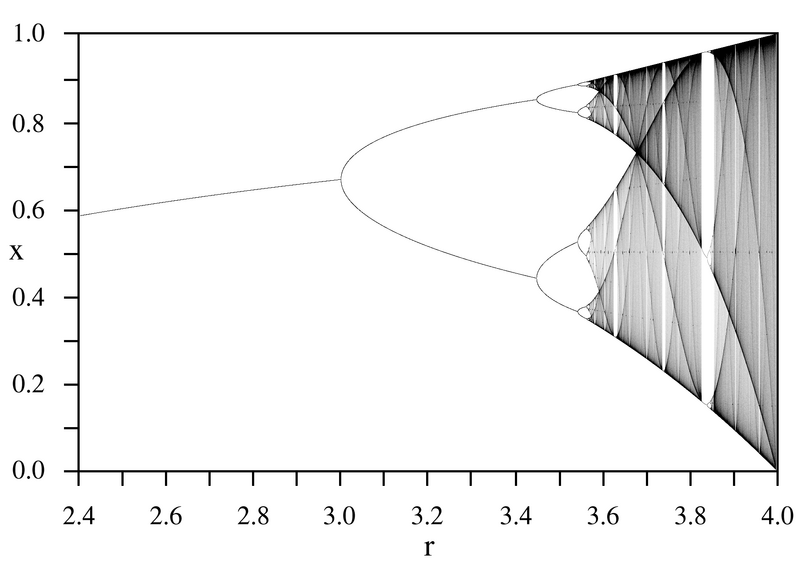
Aquí tenemos los puntos estables finales en el eje vertical y los valores del parámetro r en el eje horizontal.
Para r entre 0 y 3 tenemos un único valor para punto final estable que va aumentando poco a poco.
Justo para r=3 el periodo se dobla y el sistema oscila entre dos valores estables.
Para valores de r entre 3 y 4 el periodo se va doblando una y otra vez y cada vez más rápido con la variación del parámetro.
Para r=4 entramos en el reino del caos, ya no hay ningún periodo, nunca se vuelve a un punto anterior.

¿Y la mariposa? ¿Qué pasa con la mariposa?


Cuando se habla de caos es difícil no hablar de mariposas, somos así de tiernos. 
Una mariposa aletea en Nueva Zelanda y se produce una granizada en Murcia.
Una bonita forma de decir que una pequeña variación en las condiciones iniciales de un sistema hace que la evolución del mismo varíe muchísimo. 
En los casos que hemos visto anteriormente hemos pasado a un régimen caótico en r=4.
 ¿Podemos ver la sensibilidad a las condiciones iniciales?
  La respuesta es afirmativa.
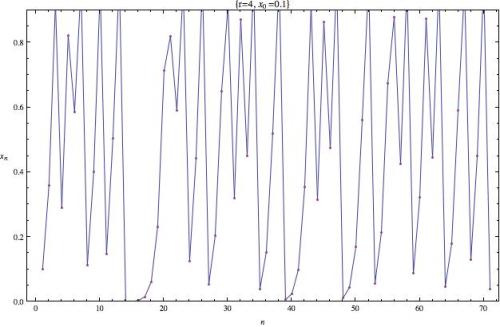
Vamos a graficar de forma superpuesta la evolución para una aplicación logística con r=4.
 Pero las condiciones iniciales las tomaremos 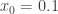x_0=0.1 y x_0=0.101. 
Y lo que obtenemos es:
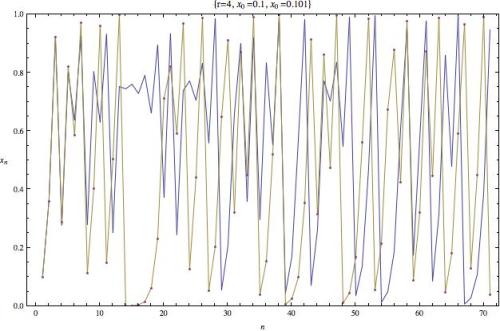
sensibilidad
¡Impresionante! ¿qué no?

Vemos como al principio las curvas se superponen pero rápidamente las gráficas se hacen muy distintas. 
Esto es la sensibilidad a las condiciones iniciales en estado puro.
 Bienvenidos al caos.

Concluyendo


Es evidente que la teoría del caos es muy amplia y con muchos detalles matemáticos, muchos de ellos de una gran profundidad y no carentes de dificultad. 
Sin embargo, es posible para todo el mundo jugar con el caos porque la propia matemática nos regala sistemas muy simples en los que el caos se pone de manifiesto.
Con esta entrada lo único que pretendíamos era picar la curiosidad de los lectores, la red está llena de aplicaciones online para jugar con la aplicación logistica y hay multitud de lecciones que servirán para profundizar en el tema. Solo hay que buscar en tu buscador favorito.
Pienso que es posible entender por lo menos los fundamentos de teorías matemáticas como el caos.
 Espero que esta entrada les haya resultado interesante.
Nos seguimos leyendo…
Publicado por en