El número e
Se relaciona con muchos interesantes resultados.
Por ejemplo, la derivada de la función exponencial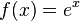 
es esa misma función.
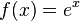es esa misma función.
El logaritmo en base 
se llama logaritmo natural o neperiano.
se llama logaritmo natural o neperiano.
El número , conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemáticoescocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.
, conocido a veces como número de Euler o constante de Napier, fue reconocido y utilizado por primera vez por el matemáticoescocés John Napier, quien introdujo el concepto de logaritmo en el cálculo matemático.
Es considerado el número por excelencia del cálculo, así como 
lo es de la geometría y el número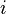 
del análisis complejo
lo es de la geometría y el número 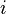del análisis complejo
El simple hecho de que la función 
coincida con su derivada hace que la función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas.
coincida con su derivada hace que la función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas.
Como consecuencia de esto, describe el comportamiento de acontecimientos físicos regidos por leyes sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto.
De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.
El número , al igual que el número y el número áureo (φ), es un irracional, no expresable por la razón de dos enteros; o bien, no puede ser expresado con un número finito de cifras decimales o con decimales periódicos.
, al igual que el número y el número áureo (φ), es un irracional, no expresable por la razón de dos enteros; o bien, no puede ser expresado con un número finito de cifras decimales o con decimales periódicos.
Además, es un número trascendente, es decir, que no puede ser obtenido mediante la resolución de una ecuación algebraica con coeficientes racionales.
e es el único número a, tal que la derivada de la función exponencial f(x) = ax (curva azul) en el punto x = 0 es igual a 1. En comparación, las funciones 2x (curva a puntos) y 4x (curva a trazos) son mostradas; no son tangentes a la línea de pendiente 1 (rojo)
es aproximadamente:
2,71828182845904523536028747135266249775724709369995…
Claro el problema es que no recuerdas más que de un par de cifras…
¿Qué hacer?
Es fácil, ve al banco y cambia unos euros por un billete de 20 dólares… pero un billete como el de la imagen.
Y memoriza el 2 (por los 20 dólares).
La imagen del billete es de Andrew Jackson, el séptimo presidente de los EE.UU. Así que memoriza el 7. Vamos por el 2,7.
Como cualquiera sabe -bueno, o casi- Jackson fue elegido en 1828, así que podemos añadir el 1828, es decir, tenemos:
2,71828.
Como hay un 2 delante de la coma, repetimos el 1828.
Tenemos la aproximación del número e:
2,718281828.
Ahora fíjate en el cuadro rojo en la cara de Jackson.
La diagonal genera dos triángulos rectángulos congruentes con ángulos de 45, 90 y 45 grados.
Por lo tanto, podemos añadir los dígitos 459045 a la aproximación del número e:
2,718281828459045.
Con esto tenemos ¡15 dígitos tras la coma decimal!
Seguro que hay otras muchas maneras de recordar estas cifras.
¿Se te ocurre alguna?
¿Eres capaz de aumentar los decimales?
