
Ya es hora de que hablemos del teletransporte cuántico.
Vamos a insistir desde el inicio que cuando hablamos de teletransporte cuántico no hablamos de hacer desaparecer algo “aquí” y volver a hacerlo aparecer “allí”.
Cuando hablamos de teletransporte cuántico nos referimos a que tenemos una partícula “aquí” y otra partícula “allí” y llevamos el estado cuántico de la partícula “aquí” a la partícula “allí”.
El fundamento de este proceso, que puede parecer increible, a mí me lo parece, reside en eso que se llama entrelazamiento. Intentaremos dar una explicación de qué es eso de entrelazamiento, que no es trivial, y tal vez no lo consiga.
Pero tenemos que intentarlo, ¿no?.
Por otro lado tenemos que comentar algo sobre el teorema de no-copiado de la mecánica cuántica y del por qué el teletransporte no está en contradicción con esta condición que nos impone la cuántica.
Para empezar, algo fácil
El cuadrado de la suma de dos númerosy
es igual al cuadrado del primero más el cuadrado del segundo más el doble del primero por el segundo.
Realmente fácil, ¿no?
Evidentemente esto lo podemos escribir de esta forma:
Tampoco hemos hecho mucho, es una manipulación bastante simple 
Ahora, vamos a poner subíndices indicando que cada uno de los factores los aporta o bien un tipo denominado 1, o bien un tipo denominado 2.
Y, como no, ahora viene una pregunta:
¿Estamos convencidos de que si alguien nos da 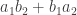 podemos concluir lo siguiente?
podemos concluir lo siguiente?
Pare que sí, ¿verdad?
Pues ya estamos listos para hablar de correlaciones y entrelazamientos 
Entrelazamiento
Ya hemos hablado varias veces sobre el principio de superposición en la cuántica.
Este principio nos dice que si un sitema puede estar en los estados  o
o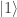 entonces puede estar en un estado
entonces puede estar en un estado  que sea un estado combinación de los anteriores:
que sea un estado combinación de los anteriores:
donde  y
y 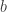 son números (pueden ser complejos) tales que se cumple:
son números (pueden ser complejos) tales que se cumple:
Lo que significa esto es lo siguiente:
- Cuando hacemos una medida sobre el sistema en el estado
el resultado nos dirá que el sistema queda en el estado
o
.
- Obtendremos
con una probabilidad
o el estado
con una probabilidad
.
Entrelazados
Imaginemos que tenemos dos sistemas como el anterior que pueden estar en un estado superpuesto con los estados  y
y 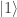 (omitimos los coeficientes a y b para simplificar las expresiones ya que no vamos a hacer cálculos explícitos).
(omitimos los coeficientes a y b para simplificar las expresiones ya que no vamos a hacer cálculos explícitos).
Ahora calculamos su producto:
¿Pero qué pasa si nos dicen que tenemos el siguiente estado?
Podemos concluir que este estado no es posible reescribirlo como el producto de un estado para el subsistema 1 y un estado para el subsistema 2:
Si nos dan el estado 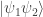 y hacemos una medida sobre el subsistema 1 obteniendo que queda en el estado
y hacemos una medida sobre el subsistema 1 obteniendo que queda en el estado 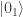 el subsistema 2 podría estar en
el subsistema 2 podría estar en  o
o 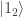 .
.
Si por el contrario, nos dan el estado  si mido en el susbsistema 1 y obtengo
si mido en el susbsistema 1 y obtengo  el subsistema 2 solo puede estar en
el subsistema 2 solo puede estar en 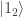 .
.
Y viceversa, si el subsistema 1 está en  el subsistema 2 estará en
el subsistema 2 estará en  .
.
Y podemos decir que estos subsistemas están entrelazados y eso se ve (matemáticamente) en que su estado no se puede escribir como el producto de estados para cada uno de los subsistemas.
Un estado se dice entrelazado si no se puede escribir como producto de los estados de los subsistemas que lo conforman.En esta situación no hay una distinción de los subsistemas. Esta correlación o entrelazamiento se verificará independientemente de la distancia entre los subsistemas.
Alicia y Bob

Tenemos dos amigos, Alicia (subsistema 1) y Bob (subsistema 2).
En un determinado momento estuvieron juntos en un laboratorio y entrelazaron un par de partículas. Es decir, el estado total de las dos partículas no se puede descomponer en el producto del estado de una de ellas por el estado de la otra.
Desgraciadamente, Alicia y Bob fueron enviados a laboratorios muy distantes entre si. Pero tuvieron el capricho de “copiar” el estado cuántico de un sistema en el que Alicia estaba trabajando del laboratorio de Alica al laboratorio de Bob.
¿Cómo pueden hacer eso? Pues siguiendo estos pasos:
- Alicia tiene un sistema S en un estado cuántico que desconoce. Pero también tiene parte del sistema entrelazado con Bob.
- Bob solo tiene su parte del sistema entrelazado con Alicia.
- Alicia hace una medida sobre su sistema S y su parte del sistema entrelazado. Al efectuar esta medida se produce un cambio en el estado del sistema S y en el de su parte del sistema entrelazado.
- Ella mira los resultados de esta medida y deduce como ha cambiado la parte del sistema entrelazado que tiene Bob.
- Alicia llama por teléfono a Bob y le comunica el resultado.
- Una vez que Bob recibe la llamada sabe en qué estado está su trozo de sistema entrelazado sin haberlo tenido que tocar.
- Con esa información recibida por teléfono Bob deduce qué acciones tiene que hacer sobre su parte del estado originalmente entrelazado para tenerlo en el estado S del sistema de Alicia.
Con estos pasos hemos conseguido llevar el estado cuántico de un sistema S desde el laboratorio de Alicia hasta el laboratorio de Bob, sin importar la distancia.
Aquí surgen un par de cuestiones:
- ¿Se ha transmitido información instantánea desde Alicia a Bob?
- ¿Se ha copiado el estado de Alicia en el laboratorio de Bob?
La respuesta a la primera pregunta es NO el estado solo se recupera cuando Alicia llama a Bob por teléfono. Es decir, tiene que decirle lo que hacer por algún medio clásico para que el teletransporte se pueda realizar.
La respuesta a la segunda pregunta es NO, Alicia al hacer la primera medida destruye su estado. El sistema S ya no está en el estado original, por tanto Bob reconstruye ese estado en otra parte pero el original ya no existe.
No hay problema con el teorema de no-copiado de la mecánica cuántica.
Como hemos visto, para hacer el teletransporte tenemos que tener tres partículas (como mínimo) para llevarlo a cabo. Las cosas no desaparecen y aparecen en otro sitio, lo que se transporta es la información acerca de un estado cuántico.
Por lo tanto, yo no me metería en un teletransportador 

Nos seguimos leyendo…