viernes, 6 de septiembre de 2013

Prohibido conmutar I (30356)


Uno de los hechos más característicos de la mecánica cuántica es la imposibilidad de determinar simultáneamente con toda precisión algunos pares de observables. 
Esta es la base del principio de indeterminación de Heisenberg.
Seguramente que cada uno de nosotros ha leído y/o estudiado eso de que no se puede conocer a la vez la posición y el momento (producto de masa por velocidad) de una partícula cuántica.
¿Qué pasaría si esto ocurriera con las coordenadas de un espacio?
 ¿Qué pasaría si por ejemplo en el plano no pudiéramos determinar simultáneamente la coordenada x y la coordenada y con total precisión?
Si esto ocurriese nos enfrentaríamos a tener geometrías no conmutativas. Este tipo de geometrías han sido desarrolladas por los matemáticos y han sido empleadas en teorías físicas.
 El ejemplo que podríamos poner es la teoría de cuerdas, sin embargo, en esta entrada veremos que hay situaciones físicas mucho más cotidianas donde esta idea se manifiesta de manera natural.
 Así que aprovecharemos las siguientes entradas para hablar un poco de geometría no conmutativa, esencialmente de su idea principal y presentaremos un ejemplo nada exótico donde se pone de manifiesto (en la siguiente entrada). 
Espero que les interese.
Hoy nos toca hablar de indeterminación y de no conmutatividad.

Principio de Indeterminación

Para empezar veamos la famosa expresión del sacrosanto principio de indeterminación de Heisenberg para la posición y el momento.
Lo que significa esta expresión es lo siguiente:
  • Cuando determinamos la posición de una partícula cuántica, extrayéndola del estado cuántico de la misma, generalmente no nos da un valor exacto sino que viene acompañada con una indeterminación asociada. Esta indeterminación, un intervalo en el que puede estar la partícula, está representada por \Delta x.
  • Si en vez de la posición intentamos determinar el momento de la partícula nos encontramos en una situación análoga. La indeterminación en el momento viene representada por \Delta p.
  • El principio de indeterminación nos dice que el producto de ambas indeterminaciones tiene que ser mayor o igual que una determinada cantidad, en este caso \hbar/2.
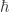Si uno mejora la indeterminación en la posición aumenta la misma para el momento y viceversa de forma que el producto siempre es igual o mayor a \hbar/2.  Recordemos que la constante \hbar es la constate de Planck dividida por 2\pi, es la llamada constante reducida de Planck.
Una visión geométrica
Supongamos que estamos estudiando una partícula que se mueve en una dimensión, una línea recta por ejemplo.
 Para determinar la forma en la que la partícula se mueve, en física clásica, determinamos sus posiciones y sus momentos de forma exacta y simultáneamente.
Si uno construye un espacio donde en un eje dispone las posiciones y en el otro eje dispone el momento de la partícula que estamos moviendo, en la mecánica clásica está perfectamente permitido determinar un punto en este espacio:
Según la física clásica podemos determinar simultáneamente posiciones y momentos así que en el espacio de fases podemos identificar puntos. Para una partícula moviéndose en una dimensión podemos construir un espacio de dos dimensiones, donde un eje es para las posiciones y el otro eje es para los momentos. A este espacio se le denomina espacio de fases.
Para una partícula moviéndose en una dimensión podemos construir un espacio de dos dimensiones, donde un eje es para las posiciones y el otro eje es para los momentos. A este espacio se le denomina espacio de fases.
 Según la física clásica podemos determinar simultáneamente posiciones y momentos así que en el espacio de fases podemos identificar puntos.
La mecánica cuántica, a causa del principio de indeterminación, lo que nos dice es que en este espacio uno no puede localizar este punto en un área menor que \hbar/2.
indeter
Dicho de otra forma, el área dada por el producto de indeterminaciones en posiciones y momentos, tiene que ser mayor o igual a esa cantidad. 
Así que, si uno disminuye la indeterminación en la posición, la del momento necesariamente tiene que aumentar.
indeter2
Por supuesto que uno puede hacer medidas de la posición con indeterminación nula, pero entonces, el principio de indeterminación nos dice que el momento de la partícula está totalmente indeterminado.

indeter3
Aquí hay una ‘magia’ matemática, cuando tengo el producto de dos factores, acotado por abajo, y quiero llevar uno de esos factores a cero manteniendo el producto acotado, el otro factor necesariamente se hace infinito. 

El punto está en que matemáticamente el producto 0\times \infty puede ser mayor o igual a una constante elegida, es lo maravilloso de los límites.

Esta discusión se puede realizar de manera análoga para el momento.
No eres torpe es que está indeterminado
Hay una idea muy extendida acerca del principio de indeterminación que nos induce a pensar que las indeterminaciones en las magnitudes físicas de la cuántica están asociadas a nuestra torpeza experimental. 
Es muy cierto que en todos los experimentos cometemos errores que nos proporcionan indeterminación en nuestras medidas. Sin embargo, en este contexto hay que recalcar lo siguiente:
El principio de indeterminación es una característica inherente a los sistemas cuánticos. No es que no podamos determinar experimentalmente de forma simultánea posiciones y momentos por incompetencia o falta de medios técnicos.
Lo que nos dice este principio es que ESTE PAR DE MAGNITUDES NO ESTA DEFINIDO SIMULTÁNEAMENTE.  Y no podríamos mejorar esta situación aunque tuviéramos metodologías experimentales perfectas que no introdujeran errores ajenos a esta circunstancia.

El origen de la indeterminación: No conmutes


En matemáticas elementales la propiedad conmutativa parece universal. Luego uno va creciendo y se encuentra con cosas que no conmutan cuando se opera con ellas de determinada manera. 
Si te has encontrado con las matrices en tus estudios estarás sonriendo ahora mismo, (no te preocupes tu cam está apagada, creo).

Se puede definir un objeto llamado conmutador que justamente pone de relieve si un par de magnitudes conmutan o no. 
 El conmutador se define del siguiente modo:
\left[A,B\right]=AB-BA
Evidentemente si el par de magnitudes A, B cumple que: \left[A,B\right]=0 
se dice que conmutan y si \left[A,B\right]\neq 0 se dice que no conmutan.
El principio de indeterminación recibe ese nombre por razones históricas, porque en realidad es un teorema, es decir, se puede probar que es cierto dentro de las hipótesis iniciales de la teoría (confirmadas experimentalmente hasta la fecha.
El teorema nos dice que el producto de la indeterminaciones a la hora de calcular las magnitudes A y B, \Delta A, \Delta B verifica lo siguiente:
\Delta A \Delta B\geq \dfrac{1}{2}|\langle\left[A,B\right]\rangle|
Aquí es donde se pone de manifiesto la relación entre indeterminación de observables y su conmutación.
Debería de estar claro que si trabajamos con un par de observables que conmuten esta expresión sería:
\Delta A\Delta B\geq 0
Lo que implica que podríamos hacer cero, simultáneamente, ambas indeterminaciones.
Toda la raíz del principio de indeterminación se encuentra en la no conmutatividad de algunas magnitudes físicas.
Posición y momento
En cuántica la relación de conmutación entre x y p viene dada por:
\left[x,p\right]=i\hbar
Para una prueba pedestre de este resultado: Cuantización Canónica.
Dado que no conmutan entre sí tendremos:
\Delta x\Delta p \geq \dfrac{1}{2}|i\hbar|
  • El valor absoluto de |i\hbar|=|i||\hbar|.
  • \hbar es una cantidad positiva así que |\hbar|=\hbar.
  • El valor absoluto de la unidad imaginaria es |i|=|\sqrt{-1}|=+\sqrt{|-1|}=\sqrt{1}=1.
Por tanto obtenemos el resultado famoso:
\Delta x\Delta p \geq \dfrac{\hbar}{2}

La no conmutatividad es más común de lo que podemos imaginar

Todo esto puede parecer un poco abstracto, lo es, pero no es menos cierto que hay operaciones que no conmutan y que las puede ver en cosas que uno puede tener a mano.
¿Tienes un libro a mano?
¿Ya?
Ok, pues dispongamos el libro en una mesa en su sentido de lectura natural:
primera
Ahora gíralo 90º hacia la izquierda.
segunda
Giramos una vez más 90º hacia arriba:
tercera
Aquí hemos hecho dos operaciones matemáticas, girar hacia la izquierda y girar hacia arriba. Cambiemos el orden, giraremos primero hacia arriba y posterior mente hacia la izquierda, la secuencia queda:
Original:
primera
Girado hacia arriba:
cuarta
Girado hacia la izquierda:
quinta
El resultado, parece evidente que no es el mismo que en el caso anterior.
 Por tanto estas operaciones, que como ven se pueden realizar en casa, no conmutan entre sí. (En este proceso, el libro no ha sufrido ningún daño).

¿Que pasa si imponemos que las coordenadas no conmuten?

Uno puede hacer la pirueta matemática de imponer que sean las propias coordenadas de un espacio las que no conmuten entre si. 
Es un concepto sutil, su estudio da lugar a lo que se conoce como geometría no conmutativa.
En principio, uno puede imponer que el conmutador entre la coordenada x y la coordenada y de un plano no conmuten:
\left[x,y\right]=i\theta
Esto se puede hacer por simple imitación de la no conmutatividad de la mecánica cuántica, donde en este caso \theta es una constante.
Pues bien, en la próxima entrada veremos como este caso de hecho se da en física. Y no, no vamos a hablar de física especulativa, de teorías de gran unificación, de supercuerdas, es un caso muy simple y fácil de conseguir donde las partículas de interés, que constituyen el sistema, viven de forma efectiva en un plano no conmutativo.
 No te pierdas la próxima entrega de este tema.
Nos seguimos leyendo…
Publicado por en