La Teoría de Probabilidades es una rama de las matemáticas que se centra en el análisis de lo esperables que pueden ser un conjunto de sucesos, útil para estimar posibles comportamientos promedios de la naturaleza, así como la economía o el mundo de los juegos de azar.
Cuando estudiamos un suceso, definimos como Espacio Muestral los posibles resultados del mismo: E {a1, a2, a3, …, an}.
σ-Álgebra:
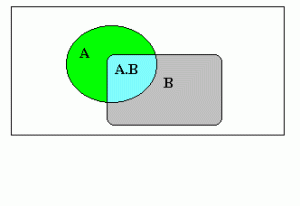
Aplicada a un Espacio Muestral, definimos como σ-Álgebra al álgebra que define 3 operaciones en “E”, que son la unión “U“, la intersección “∩” y la negación “‾”, bajo las cuales el Espacio Muestral es cerrado. Si consideramos los subconjuntos “Ai” de “E” y los elementos “ai” del mismo, se cumple:
.-”Ai U Aj” es el conjunto de elementos “ai” que o bien pertenecen a “Ai” o bien pertenecen a “Aj”.
.-”Ai ∩ Aj” es el conjunto de elementos “ai” que pertenecen a “Ai” y también a “Aj”.
.-”Ai‾” es el conjunto de elementos “ai” que no pertenecen a “Ai”.
La σ-Álgebra cumple las siguientes propiedades:
.-El vacío “ø” pertenece al Espacio Muestral “E”.
.-Si “Ai” pertenece a “E”, “Ai‾” también.
.-U(Ai) desde “i = 1″ hasta “n” pertenece a “E”. (La unión numerable de subconjuntos de “E” pertenece a “E”). Si unimos todos los subconjuntos Ai posibles obtendremos, evidentemente, el propio Espacio Muestral.
Espacio de Probabilidad:
El Espacio Muestral “E” toma valores en el Espacio de Probabilidad, contenido en el intervalo [0, 1], de tal modo que a cada subconjunto “Ai” le corresponde una determinada probabilidad “p(Ai)” contenida en el mencionado Espacio de Probabilidad. Si la probabilidad de un suceso es “1″ se dará siempre, si es nula no se dará nunca, y en cualquier otro caso puede acontecer o no.
Podemos interpretar la probabilidad técnicamente como el límite de la frecuencia relativa de los elementos de una Muestra cuando el número de los mismos tiende a infinito.
- p(Ai) = lim(N→∞) n(Ai) / N.
En caso de que no dispongamos de ninguna muestra analizada, hay otras formas de intuir la probabilidad, como es el caso de la Regla de Laplace:
- p(Ai) = nº casos favorables / nº casos posibles.
En caso de que no sepamos nada sobre el experimento y dispongamos del Espacio Muestral, el Principio de Razón Insuficiente o de Máxima Entropía nos explica que todos los casos son igual de favorables:
- p(Ai) = 1 / n.
Podemos, en resumen, definir la probabilidad como una medida del grado de certidumbre sobre un suceso en un experimento aleatorio, o como una medida de información sobre el mismo.
Axiomas de Kolmogorov:

Siempre que estemos ante un fenómeno aleatorio definido en un espacio muestral “E”. La representación a través de la función “p” que lleva cada elemento “Ai” de “E” al Espacio de Probabilidad es una medida de probabilidad si se verifica que:
- 0 ≤ p(Ai) ≤ 1.
, que la probabilidad de “E” es 1, o sea, es un suceso seguro:
- p(E) = 1.
, y que si “Ai” y “Aj” son sucesos mútuamente excluyentes:
- Ai ∩ Aj = ø.
- p(Ai U Aj) = p(Ai) + p(Aj).
Algunas otras propiedades son:
- p(Ai‾) = 1 – p(Ai).
- p(Ai U Ai‾) = p(E) = 1.
- p(Ai ∩ Ai‾) = 0.
- p(Ai U Aj) = p(Ai) + p(Aj) – p(Ai ∩ Aj).
Para evaluar prácticamente la probabilidad de un suceso desconocido debemos realizar experimentos, analizarlos teóricamente aplicando el Principio de Máxima Entropía, y combinar la teoría con la experiencia.
Definimos Probabilidad Marginal como la de un subconjunto de “E”, es decirm a “p(Ai)”, Probabilidad Conjunta de dos subconjuntos “Ai” y “Aj” como la de su intersección: p(Ai ∩ Aj), cumpliéndose que la Probabilidad Marginal de un elemento es igual a la suma de sus Probabilidades Conjuntas con los otros “n” subconjuntos mútuamente excluyentes:
- p(Ai) = ∑(p(Ai ∩ Aj)) desde “j = 1″ hasta “n”.
La Probabilidad Condicionada es la probabilidad de que se de un suceso “Ai” sabiendo que se ha dado otro “Aj”:
- p(Ai / Aj) = p(Ai ∩ Aj) / p(Aj).
- p(Ai / Aj) ≠ p(Aj / Ai).
Hablamos de Independencia Estadística entre dos subconjuntos “Ai” y “Aj” cuando, siendo ambos aleatorios, se cumple:
- p(Ai / Aj) = p(Ai).
- p(Aj / Ai) = p(Aj).
También enunciable como:
- p(Ai ∩ Aj) = p(Ai) p(Aj).
Teorema de Bayes:
Si disponemos de un experimento aleatorio en dos etapas de espacios muestrales {Aa, A2, …, An} y {B1, B2, …, Bm}, y conozco todos los posibles valores de p(Bj / Ai), se cumple que:
- p(Ai / Bj) = (p(Bj / Ai) p(Ai)) / (∑(p(Bj / Ak) p(Ak)) desde “k = 1″ hasta “n”).
Variables Aleatorias Discretas:
Si nuestro Espacio Muestral “E” toma valores numerables en la recta real, o puede ser asociado a ellos, estamos ante una variable aleatoria discreta, donde E{x1, x2, …, xn}.
.-Función de Probabilidad:
La probabilidad de que un suceso tome el valor “xi” se define como:
- p(x = xi) = pi.
- 0 ≤ pi ≤ 1.
- ∑(p(x = xi)) desde “i = 1″ hasta “n” = ∑(pi) desde “i = 1″ hasta “n” = 1.
.-Distribución Uniforme:
Si todos los posibles valores “xi” poseen una misma probabilidad de acontecer hablamos de una distribución de probabilidad uniforme:
- pi = p(x = xi) = 1 / n.
.-Función de Distribución de Probabilidad:
Si definimos “F(xk)” como la función que determina la probabilidad de que un suceso tome un valor menor o igual a “xk” obtenemos la siguiente igualdad:
- F(xk) = p(x ≤ xk) = ∑(p(x = xj)) desde “j = 1″ hasta “k”.
- F(x) = 0, si el suceso toma un valor menor a “x1″.
- F(xn) = 1.
“F(xk)” es una función monótona creciente.
Variable Aleatoria Continua. Función de Densidad de Probabilidad:
Si nuestro Espacio Muestral “E” toma valores no numerables en la recta real, o puede ser asociado a ellos, estamos ante una variable aleatoria continua, donde el Espacio Muestral es infinito. Esta inmensa cantidad de posibles resultados “xi” hace que la probabilidad particular de cada uno de ellos sea “0″, pues cada “xi” lleva asociada una probabilidad “p(x)” tal que:
- dp(x) = f(x) dx.
, siendo f(x) la Función de Densidad de Probabilidad, que indica la probabilidad particular de cada suceso:
- f(x) = dp(x) / dx.
.-Paso al Continuo:
Si en la variables discretas el espacio muestra se podia definir como:
- E = ∑ desde “i = 1″ hasta “n”.
, en la variable continua nos encontramos con que:
- E = ∫(dx) en el Espacio Muestral = ∫(dx) desde “- ∞” hasta “∞”.
.-Distribución de Probabilidad:
Al ser “E” continuo, debemos redefinir la función de probabilidad:
- p(a ≤ x ≤ b) = ∫(dp(x)) desde “a” hasta “b” = ∫(f(x) dx) desde “a” hasta “b”.
.-Función de Distribución Acumulativa:
Es fácil redefinirla también a partir de la discreta:
- F(x0) = p(x ≤ x0) = ∫(f(x) dx) desde “- ∞” hasta “x0″.
- lim(x0→-∞) F(x0) = 0.
- lim(xo→∞) F(x0) = 1.
A través del Teorema fundamental del cálculo integral, obtenemos:
- dF(x) / dt = f(x).
Medidas Características de una Distribución de Probabilidad para una Variable Aleatoria Discreta:
.-Espacio Muestral:
- E = {A1, A2, …, An}
para “n” elementos.
.-Sucesos:
A través de la función “x(Ai)” denominamos a los elementos de “E” como el suceso tal que:
- x(Ai) = xi.
.-Función de Probabilidad:
Definimos “p(xi)” como la función que da a un suceso el valor de su probabilidad (en el Espacio de Probabilidad):
- p(xi) = pi.
.-Medidas de Centralización:
..-Moda:
La moda es el suceso “xi” con mayor probabilidad.
..-Mediana:
La mediana es el suceso “xi” que toma el valor 0,5 en la función de distribución acumulativa, es decir:
- F(xi) = 0,5.
..-Media o Valor Esperado:
- E{x} = ∑(pi xi) desde “i=1″ hasta “n” = μ.
.-Medidas de Dispersión:
..-Varianza:
- σ^2 = E{(x – μ)^2} = ∑(pi (xi – μ)^2) desde “i = 1″ hasta “n”.
..-Desviación Típica:
- σ = (σ^2)^1/2.
..Función Generatriz de Momentos:
- mr(c) = E{(x – c)^r} = ∑(pi (xi – c)^r) desde “i=1″ hasta “n”.
Hablaremos de momentos respecto al origen y centrales si se cumple:
- c = 0.
- c = μ.
respectivamente.
Medidas Características de una Distribución de Probabilidad para una Variable Aleatoria Continua:
.-Espacio Muestral:
En esta ocasión abarca todo el conjunto de los números reales.
- E = R.
.-Sucesos:
- x(Ai) = xi.
.-Función de Probabilidad:
Definimos “f(x)” como la función que da a un suceso el valor de su probabilidad (en el Espacio de Probabilidad):
- f(xi) = pi.
Cumple que:
- ∫(f(x) dx) desde “- ∞” hasta “- ∞” = 0.
- ∫(f(x) dx) desde “- ∞” hasta “∞” = 1.
.-Medidas de Centralización:
..-Moda:
La moda es el suceso “xi” con mayor probabilidad. Cumple que:
- f’(xi) = 0.
- f”(xi) < 0.
..-Mediana:
La mediana es el suceso “xi” que toma el valor 0,5 en la función de distribución acumulativa, es decir:
- F(xi) = 0,5.
..-Media o Valor Esperado:
- E{x} = ∫(x dp(x)) desde “- ∞” hasta “∞” = ∫(f(x) x dx) desde “- ∞” hasta “∞” = μ.
.-Medidas de Dispersión:
..-Varianza:
- σ^2 = E{(x – μ)^2} = ∫(f(x) (xi – μ)^2 dx) desde “- ∞” hasta “∞”.
..-Desviación Típica:
- σ = (σ^2)^1/2.
..Función Generatriz de Momentos:
- mx(t) = E{e^(t x)} = ∫(f(x) e^(t x) dx) desde “- ∞” hasta “∞”.
- e^(t x) = h(x).
- mx(t) = E{h(x)} = ∫(f(x) h(x) dx) desde “- ∞” hasta “∞”.
Distribución Binomial:

La probabilidad de que se de un determinado suceso en un experimento sigue una distribución binomial si cumple los requisitos de ser un experimento de Bernoulli, es decir, que sea un fenómeno con dos posibles sucesos mútuamente excluyentes. Uno de los sucesos será el éxito: “A”, y el otro el fracaso: “B”. Obtenemos así nuestro espacio muestral y nuestros sucesos:
- E = {A, B}.
- x(A) = 1.
- x(B) = 0.
La distribución de probabilidad, que veremos ahora en detalle, cumplirá los axiomas elementales de nuestra σ-Álgebra, teniendo en cuenta la nueva nomenclatura:
- p(A) = p.
- p(B) = 1 – p(A) = q.
Si consideramos una variable “x” que represente el número de sucesos, su espacio muestral será el conjunto de los números naturales (1 éxito, 2 éxitos, 3 éxitos…), y la probabilidad de obtener “n” éxitos la denominamos como: p(x=r).
La media o esperanza de la distribución binomial y su varianza son:
- μ = E{x} = p 1 + q 0 = p.
- σ^2 = E{x – E{x}} = p (1 – p)^2 + q (0 – p)^2 = p (1 – p) = p q.
Y su distribución de probabilidad para “n” experimentos es:
- p(x = r) = (n|r) p^r q^(n – r).
, donde (n|r) representa un número combinatorio derivado del binomio de Newton, y que se define por:
- (n|r) = n! / (r! (n – r)!).
- r ≤ n.
Recordemos que el factorial de un número entero “n!” no es más que el producto del mismo por todos y cada uno de los enteros menores que él.
Si queremos normalizar la distribución, entre otras cosas, debemos asegurarnos de que cumple con los axiomas de Kolmogorov, sobre todo el de que la suma de todas las probabilidades de todos los posibles de “r” para un determinado valor “n” de experimentos sumen 1:
- ∑(p(x = r)) desde “r = 0″ hasta “n” = ∑((n|r) p^r q^(n – r)) desde “r = 0″ hasta “n”.
Por simetría con el binomio de Newton:
- ∑(p(x = r)) desde “r = 0″ hasta “n” = (p + q)^n = 1^n = 1.
Se cumple el axioma de Kolmogorov.
Calculemos ahora la media o esperanza matemática para un valor dado de “n”:
- E{x} = ∑(pi xi) desde “i = 1″ hasta “n”.
- E{x} = ∑(r (n|r) p^r q^(n – r)) desde “r = 0″ hasta “n”.
- E{x} = ∑(r (n|r) p^r q^(n – r)) desde “r = 1″ hasta “n”.
Haciendo un cambio de variable:
- r’ = r – 1.
- n’ = n -1.
Y operando:
- E{x} = n p.
La varianza, y consecuentemente la desviación típica, son algo más complejas de calcular, por lo que obviaremos pasos intermedios:
- σ^2 = E{x^2} – E{x}^2 = n p q.
- σ = [n p q]^1/2.
1ª Variable de Pascal o Geométrica:

En un experimento de Bernoulli definimos una nueva variable “x” que medirá el número de éxitos antes de el primer fracaso, por lo que su Espacio Muestral “E” tomará valores naturales: 0, 1, 2…, y aplicando la distribución binomial obtenemos que la probabilidad de que el número de éxitos “x” antes del primer fracaso sea igual a “r” es:
- p(x = r) = p^r q.
Se cumple:
- ∑(p(x = r)) desde “r = 0″ hasta “∞” = 1.
- E{x} = p / q.
- σ^2 = p / q^2.
- σ = p^1/2 / q.
2ª Variable de Pascal o Geométrica:
De nuevo en un experimento de Bernoulli, esta vez definiremos una variable “x” que indicará el número de intentos hasta el primer fracaso, por lo que su Espacio Muestral tomará los mismos valores que en el caso anterior menos el “0″ (no se pueden hacer 0 intentos y fracasar). En esta ocasión:
- p(x = r) = p^(r – 1) q.
Y se cumple:
- ∑(p^(r – 1) q) desde “r = 1″ hasta “∞” = 1.
- E{x} = 1 / q.
- σ^2 = p / q^2.
- σ = p^1/2 / q.
Ley de los Grandes Números:
Supongamos una variable binomial “A”que, muestra a muestra, resulta poseer una frecuencia relativa “fA” aleatoria, y sea “f(fA)” la función de probabilidad de que tome un valor concreto. Si definimos el valor esperado de fa “E{fA}” como el estimador más fiel del valor de la misma, y lo calculamos haciendo “N” experimentos, cuando el número de los mismos tienda a infinito veremos que:
- E{fA} = p(A).
Veamos si se cumple:
- fi = nA / N.
, siendo “ni” la frecuencia absoluta (número de veces que aparece en total).
- E{fA} = E{nA / N} = E{nA} / N = N pA / N = p(A).
Vemos que la igualdad se cumple.
Comprobemos qué sucede con la varianza:
- σ(fA)^2 = σ(nA / N)^2 = σ(nA)^2 / N^2.
Por ser una variable binomial:
- σ(fA)^2 = N p q / N^2 = p q / N.
Si el número “N” de experimentos tiende a infinito, concluimos que la varianza de nuestra media tiende a “0″, y que por tanto nuestro valor de la probabilidad es exacto:
- lim(N→∞) σ(fA)^2 = lim(N→∞) pq / N = 0.
Distribución de Poisson:

Siguen una distribución de probabilidad de este tipo todos aquéllos experimentos en los que una variable discreta tiene lugar sobre un soporte continuo (espacio-tiempo). Algunos ejemplos son las llamadas a una central de averías o el bombardeo de una lámina de oro con neutrones.
Tiene que ser un proceso estable, en el que más o menos se establezca un valor medio representativo de la variable, y los sucesos han de surgir continuamente de manera independiente.
Nuestra variable “x” (número de sucesos por intervalo continuo) tomará valores en el Espacio Muestral “E” de los números enteros {0, 1, 2, …}, y si los posibles valores de “x” tienden a infinito la probabilidad de cada uno de ellos tiende a “0″. Definimos la media “λ” como:
- λ = n p.
- lim(n→∞) p = 0.
La probabilidad de que en un intervalo concreto la variable “x” tome un valor “r” es:
- p(x = r) = (n|r) p^r q^(n – r) = (n|r) p^r (1 – p)^(n – r).
Aplicando la igualdad anterior:
- lim(n→∞) (n|r) (λ / n)^r (1 – λ / n)^(n – r) = lim(n→∞) p(x = r).
- lim(n→∞) p(x = r) = λ^r e^(- λ) / r!
, que es la disribución de la archifamosa ecuación de la distribución de Poisson.
Veamos que cumple el tercer axioma de Kolmogorov:
- ∑(p(x = r)) desde “r = 0″ hasta “∞” = ∑(λ^r e^(- λ) / r!) desde “r = 0″ hasta “∞”.
- ∑(p(x = r)) desde “r = 0″ hasta “∞” = e^(- λ) ∑(λ^r / r!) desde “r = 0″ hasta “∞”.
- ∑(p(x = r)) desde “r = 0″ hasta “∞” = e^(- λ) e^(λ) = e^0 = 1.
Lo cumple.
Analicemos ahora el valor esperado:
- ∑(p(x = r) r) desde “r = 0″ hasta “∞” = ∑(λ^r e^(- λ) r / r!) desde “r = 0″ hasta “∞”.
- ∑(p(x = r) r) desde “r = 0″ hasta “∞” = λ ∑(λ^(r – 1) e^(- λ) / (r – 1)!) desde “r = 1″ hasta “∞”.
- ∑(p(x = r) r) desde “r = 0″ hasta “∞” = λ e^(- λ) e^(λ) = λ.
La varianza tendrá la peculiaridad de ser igual a la media:
- σ^2 = E{x^2} – E{x}^2 = λ.
Y el Coeficiente de Variación:
- CV = σ / E{x} = λ^1/2 / λ = 1 / λ^1/2 = 1 / (n p)^1/2 ≈ 1 / n^1/2.
Distribución Exponencial:
Si suponemos un proceso de Poisson de media “λ”, y queremos definir la variable “t”, tiempo entre dos sucesos, dicha variable será continua y tomará valores en el intervalo [0, ∞). Si queremos calcular la probabilidad de que "t" tome un valor mayor que "t0", su distribución de probabilidad se define como:
- p(t > t0) = p(x = 0 en (0, t0)) = (λ t0)^0 e^(λ t0) / 0! = e^(λ t0).
, de ahí que se la denomine distribución exponencial.
Análogamente, la probabilidad de que "t" sea menor o igual que un determinado "t0" se define como:
- p(t ≤ t0) = 1 - p(t > t0) = 1 - e^(λ t0).
Otras características son:
- F(t) = 1 - e^(λ t).
- f(t) = dF(t) / dt = λ e^(λ t).
Distribución Gaussiana o Normal:
Supongamos una variable aleatoria continua (de cualquier valor numérico real) que posea una media "μ" y una desviación típica "σ". Decimos que estamos ante una Variable Aleatoria Normal N(μ, σ) si su distribución de probabilidad es:
- f(x) = e^((x - μ)^2 / (2 σ^2)) / ([2 π]^1/2 σ).
Esta función, que como se aprecia en la representación tiene forma de campana, es la conocida Campana de Gauss, cuyo valor central toma el valor “μ”, y posee puntos de inflexión en los puntos “μ – σ” y “μ + σ”.
La función Acumulativa de esta distribución se define como:
- F(x0) = ∫(e^((x – μ)^2 / (2 σ^2)) dx / ([2 π]^1/2 σ)) desde “- ∞” hasta “x0″.
Y la probabilidad de que “x” tome valores en el intervalo [a, b] es de:
- p(a ≤ x ≤ b) = ∫(e^((x – μ)^2 / (2 σ^2)) dx / ([2 π]^1/2 σ)) desde “a” hasta “b”.
El problema de esta función de densidad de probabilidad reside en que no es integrable, y por tanto los valores de su primitiva se deben tantear por métodos numéricos. Asimismo, como hay infinidad de distribuciones gaussianas según sus valores de “μ” y de “σ”, necesitamos buscar una relación entre todas ellas para estudiarlas todas de golpe.
Llamamos proceso de Normalización o Tipificación al proceso mediante el cual convertimos cualquier variable aleatoria N(μ, σ) a una N(0, 1). Para ello, definimos un parámetro “z” tal que:
- z = (x – μ) / σ.
De modo que:
- f(x) = e^(z^2 / 2) / [2 π]^1/2.
Cualquier función normal tipificada de este modo se denomina Variable Aleatoria Estándar, y su distribución de probabilidad es:
- p(a ≤ x ≤ b) = p((a – μ) / σ ≤ x ≤ (b – μ) / σ) = F((b – μ) / σ) – F((a – μ) / σ).
La Función Generatriz de Momentos de la Gaussiana Estándar se define como:
- mz(t) = E{e^(z t)}.
- mz(t) = ∫(e^(z t) e^(z^2 / 2) dz / [2 π]^1/2) desde “- ∞” hasta “∞”.
- mz(t) = e^(t^2 / 2).
Teorema del Límite Central:
Supongamos una variable “X” definida com0:
- X = x1 + x2 + x3 + x4 + x5 + … + xn.
Si cada “xi” que la compone es una variable aleatoria independiente de las demás, con una media “μi” y una desviación típica “σi”, y estos valores no son muy dispares entre cada uno de los elementos, podemos concluir que cuando el número “n” de elementos tiende a infinito la distribución de probabilidad de “X” es gaussiana.
Distribución Log-Normal:
Definamos una variable aleatoria “Y” dependiente de otras variables aleatorias “xi” independientes entre si de modo que:
- Y = x1 x2 x3 x4 … xn = Π(xi) desde “i = 1″ hasta “n”.
Consecuentemente:
- Ln(Y) = ∑(log(xi)) desde “i = 1″ hasta “n” = z.
Por el teorema antes mencionado, cuando el número de elementos “xi” tiende a infinito, “z” se vuelve una variable aleatoria normal de media “μ” y desviación típica “σ”:
- μ = ∑(log(μi)) desde “i = 1″ hasta “n”.
, por lo que su función de densidad de probabilidad es:
- f(z) = e^((z – μ)^2 / (2 σ^2)) / ([2 π]^1/2 σ).
Por otra parte, sabemos que:
- dp(z) = f(z) dz.
- dp(y) = g(y) dy.
Como ambas distribuciones son continuas sus diferenciales de probabilidad son nulos y podemos igualarlas:
- f(z) dz = g(y) dy.
- g(y) = f(z) dz / dy.
- dz / dy = dLn(y) / dy = 1 / y.
Para este último resultado aplicamos la derivada del logaritmo natural, por lo que esta “y” solo toma valores en (0, ∞), y la función de probabilidad de “y” nos resulta:
- g(y) = e^((z – μ)^2 / (2 σ^2)) / ([2 π]^1/2 σ y).
Distribución de Weibull (Gompertz):
Esta distribución analiza la probabilidad del fallo de un elemento, también enunciable como la esperanza de vida. Si definimos “t” como el tiempo que puede pasar antes de que el elemento analizado falle, evidentemente tomará valores en el intervalo (0, ∞). Su distribución genérica de probabilidad de durar “t” tiempo es:
- λ(t) = p(t0 < t ≤ t0 + Δt) = p(t0 < t ≤ t0 + Δt) / p(t > t0).
- λ(t) = f(t0) Δt / (1 – F(t0)).
Su función acumulativa es:
- Λ(t) = ∫(λ(t0) dt0) desde “0″ hasta “t”.
- Λ(t) = ∫(f(t0) Δt dt0 / (1 – F(t0))) desde “0″ hasta “t”.
- Λ(t) = – [Ln|1 - F(t0)|] desde “0″ hasta “t” = - Ln|1 – F(t0)|.
De donde:
- F(t) = 1 – e^(- Λ(t)).
- f(t) = dF(t) / dt = 1 – λ(t) e^(- Λ(t)).
Si suponemos una Tasa de Fallo Potencial o de Weibull para “h” y “c” predeterminados obtenemos:
- λ(t) = h t^(c – 1).
- Λ(t) = h t^c / c.
- f(t) = h t^(c – 1) e ^(- h t^2 / c).
Si suponemos una Tasa de Fallo Exponencial o de Gompertz para “k” y “b” predeterminados obtenemos:
- λ(t) = k e^(b t).
- Λ(t) = k (e^(b t) – 1) / b.
- f(t) = k e^(b t) e ^(- k (e^(b t) – 1) / b).