lunes, 25 de noviembre de 2013

Café matemático... Números algebraicos


Se dice que un número real x \in \mathbb R es algebraico si existe un polinomio 

p(x)=a_0+a_1x+\cdots +a_nx^n con coeficientes enteros con a_n \neq 0

tal que p(\alpha)=0.

Cualquier número racional x=a/b con a,b \in \mathbb Z y con b \neq 0 es raíz del polinomio p(x)=a-bx y por lo tanto es algebraico. 

Si \alpha \in \mathbb R es algebraico entonces existe un polinomio mónico de grado mínimo 

p(x)=a_0+a_1x+\cdots +a_{n-1}x^{n-1}+x^n 

tal que p(\alpha)=0. 

Se dice que 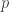p es el polinomio mínimo de \alpha.

Es obvio que \sqrt{2} y \sqrt{3} son algebraicos, pues son raíces de los polinomios
 x^2-2\; y \; x^2-3, respectivamente.
 Sin embargo, no es evidente que la suma x=\sqrt{2}+\sqrt{3} 
sea también un número algebraico. 
Veamos que esto es así. 
Tenemos (x-\sqrt{2})^2-3=0 pero no todos los coeficientes en esta expresión son enteros, por lo que consideramos la expresión conjugada (x+\sqrt{2})^2-3. 
Multiplicando ambas expresiones se cancelan los términos cuyos coeficientes no son enteros y resulta
[(x-\sqrt{2})^2-3] \cdot [(x+\sqrt{2})^2-3]=

=(x^2-2\sqrt{2} x -1)\cdot (x^2+2\sqrt{2} x -1)=x^4-10x^2+1,

de donde se obtiene el polinomio mínimo
 p(x)=x^4-10x^2+1.
El siguiente criterio indica que muchos números algebraicos son irracionales,
 como por ejemplo \sqrt{2}+\sqrt{3}.
Teorema. 
Si x \in \mathbb{R} satisface una ecuación algebraica con coeficientes enteros
\displaystyle{ x^n + a_{n-1}x^{n-1}+ \cdots + a_1x+a_0=0 }
entonces x es irracional si no es entero.
Demostración. Razonamos por reducción al absurdo.
 Suponemos que x=r/s 
con r,s \in \mathbb Z\;corrimos y con s \neq 0, \pm 1. 
Tenemos
\displaystyle{ \frac{r^n}{s^n} + a_{n-1} \frac{r^{n-1}}{s^{n-1}} + \cdots + a_1 \frac{r}{s} + a_0=0 }

y por lo tanto
\displaystyle{ (\ast) \qquad r^n =-( a_{n-1}r^{n-1} s + \cdots + a_1 r s^{n-1} + a_0 s^n). }

Como s \notin \{-1,0,1\} se sigue que s posee un divisor primo.
 Este número divide al segundo miembro de (*)
 y por lo tanto divide a r^n luego divide a r. 
Hemos llegado a la contradicción de que r,s poseen un divisor común.
Publicado por en