sobre El campo de Higgs (31865)

En la concepción del Modelo estándar de física de partículas, el bosòn de Higgs así como otros bosones (encontrados ya experimentalmente) y ligados en esta teoría, se interpretan desde el Bosón de Goldstone donde cada parte del rompimiento de simetría genera un campo, para el cual los elementos que viven en este campo son sus respectivos bosones. 

Existen teorías creadas a partir del miedo de la no existencia del bosòn de Higgs donde no es necesaria su aparición. 

El campo de Higgs es el ente matemático donde existe, su interpretación con la teoría es el producto de él con los otros campos que sale por el mecanismo de ruptura, este producto nos da el acople y la interacción de él, con esta interacción con los otros campos legamos la característica de generador de masa.

Formulación matemática

Introducimos un campo adicional ?

 que rompa la simetría SU(2)L × U(1)Y ? U(1)em.

 Debido a las condiciones que se exigen a la teoría será un doblete (de SU(2)L) de campos escalares complejos (doblete de Higgs):

 Dobletes de Higgs

El número total de entradas (número dimensional del vector) de Higgs no está determinado por la teoría y podría ser cualquiera. 

No obstante la versión mínima del SM posee uno solo de estos dobletes.

El sistema vendrá entonces descrito por un Lagrangiano de la forma:

tal que:

donde V(phi) es el potencial normal (y por tanto que mantiene la invarianza gauge) más sencillo.

 Para que se produzca ruptura espontánea de simetría es necesario que el valor esperado del campo de Higgs en el vacío sea no nulo.

 Para lambda mayor que 0, si mu 2 menor que 0, el potencial posee infinitas soluciones no nulas (ver figura 1), en las cuales sólo la norma del campo de Higgs está definida:

Estado fundamental

El estado fundamental está, por consiguiente, degenerado y no respeta la simetría del grupo SU(2)L × U(1)Y. 

Sin embargo, sí conserva la simetría del grupo U(1)em.

 El valor de cup ?

 indica la escala de energía a la que se produce la ruptura de la simetría electrodébil. La ruptura SU(2)L × U(1)Y Phi  U(1)em se produce cuando se selecciona un estado del vacío concreto.

 La elección habitual es aquella que hace que Phi 3 sea no nulo:

Espectro de partículas

El espectro de partículas físicas resultantes se construye realizando pequeñas oscilaciones en torno al vacío, que pueden ser parametrizadas en la forma:

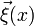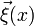donde el vector  y el escalar h(x) son campos pequeños correspondientes a los cuatro grados de libertad reales del campo . 

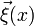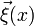Los tres campos  son los bosones de Goldstone, de masa nula, que aparecen cuando una simetría continua es rota por el estado fundamental (teorema de Goldstone).

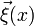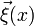En este punto aún tenemos 4 bosones gauge (Wi?(x) y B?(x)) y 4 escalares ( y h(x)), todos ellos sin masa, lo que equivale a 12 grados de libertad 

(Conviene notar que un bosón vectorial de masa nula posee dos grados de libertad, mientras que un bosón vectorial masivo adquiere un nuevo grado de libertad debido a la posibilidad de tener polarización longitudinal: 12 = 4[bosones vectoriales sin masa] × 2 + 4[escalares sin masa]). P. W. Higgs fue el primero en darse cuenta de que el teorema de Goldstone no es aplicable a teorías gauge, o al menos puede ser soslayado mediante una conveniente selección de la representación.

 Así, basta con escoger una transformación:

de forma que:

con lo cual desaparecen los tres campos de Higgs no físicos .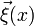

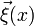 Debemos aplicar estas transformaciones sobre la suma de las Lagrangianas para bosones y fermiones:

Al final del proceso, tres de los cuatro bosones gauge adquieren masa al absorber cada uno de los tres grados de libertad eliminados del campo de Higgs, gracias a los acoplamientos entre los bosones gauge y el campo Phi presentes en la componente cinética de la Lagrangiana SBS:

Por otro lado, el vacío de la teoría debe ser eléctricamente neutro, razón por la que no existe ningún acoplamiento entre el fotón y el campo de Higgs, h(x), de forma que aquél mantiene una masa nula. Al final, obtenemos tres bosones gauge masivos (W±?, Zµ), un bosón gauge sin masa (A?) y un escalar con masa (h), por lo que seguimos teniendo 12 grados de libertad

 (del mismo modo que antes: 12 = 3[bosones vectoriales masivos] × 3 + 1[bosón vectorial sin masa] × 2 + 1[escalar]). 

Los estados físicos de los gauge" 

bosones gauge se expresan entonces en función de los estados originales y del ángulo de mezcla electrodébil ?W:

Ángulo de mezcla

El ángulo de mezcla ?W, se define en función de las constantes de acoplamiento débil, g, y electromagnética, g´, según:

Las predicciones de las masas de los bosones a nivel de árbol son:

donde (e es la carga eléctrica del electrón):

 Masa del bosón de Higgs

La masa del bosón de Higgs se expresa en función de ? y del valor de la escala de ruptura de simetría, ?, como:

La medida de la anchura parcial de la desintegración:

a bajas energías en el SM permite calcular la constante de Fermi, GF, con gran precisión.

 Y puesto que:

se obtiene un valor de ? = 246 GeV.

 No obstante el valor de ? es desconocido y por tanto la masa del Higgs" 

el bosón de Higgs en el SM es un parámetro libre de la teoría.

 Bosones gauge y fermiones

Análogamente al caso de los bosones gauge, los fermiones adquieren masa mediante los denominados acoplamientos de Yukawa, que se introducen a través de una serie de nuevos términos en la Lagrangiana:

donde:

Del mismo modo que antes, se aplica la transformación sobre la parte levógira de los fermiones, mientras que la parte dextrógira no se transforma:

Y finalmente se obtienen las masas de los fermiones según:

Es conveniente hacer notar en este punto, que la determinación de la masa del bosón de Higgs, no explica directamente las masas fermiónicas ya que dependen de las nuevas constantes ?e, ?u, ?d, … 

Por otro lado, se deduce también el valor de los acoplamientos del bosón de Higgs con los distintos fermiones y bosones, los cuales son proporcionales a las constantes de acoplamiento gauge y a la masa de cada partícula.

Ya hablaremos más sobre el tema