
Curiosamente hoy ha saltado la noticia de que han demostrado la existencia de un ser superior usando el teorema de Gödel.
Diseña tu teoría física — Crash Course
Ya ha salido el susodicho teorema para concluir que las mates y la física son incompletas y por lo tanto no podemos confiar en ellas.
Esa conclusión, partiendo del magnífico trabajo de Kurt Gödel, es tan acertada como atribuirle al Quijote la expresión:
Cosas veredes, Sancho.
Pues sí amigos, cosas veredes.
En esta entrada vamos a intentar dar unas pinceladas sobre el teorema de Gödel y sobre sus magnífica y populares malinterpretaciones.
El amigo Kurt ... la complicó.

¿Qué dijo Gödel?
¿Terminó con la utilidad de las matemáticas?
¿Las sentenció a muerte?
¿Todas las ciencias que dependan de las matemáticas están abocadas al fracaso?
Pues no, tranquilos, este hombre lo que hizo fue estudiar la matemática desde el punto de vista de su fundamento lógico. Desnudó a la matemática de todo significado y estudió las condiciones en las que la matemática se desarrollaba.
Y su trabajo fue fundamental para entender la base de la matemática y deliciosamente inútil respecto al trabajo diario de un matemático.
Así de simple y así de hermoso.
Sin embargo, sus resultados pueden que sean de los más empleados en discusiones ajenas a la matemática, casi siempre fuera de todo el contexto en el que sus teoremas tenían significado.
Los teoremas de incompletitud de Gödel, se han pervertido hasta límites insospechados. Y generalmente, todo parecido con la realidad es pura coincidencia.
¿Qué es la matemática?
La matemática no es más que una serie de afirmaciones que se prueban ciertas o falsas en términos de unas afirmaciones previas siguiendo unas reglas establecidas, partiendo de unas afirmaciones iniciales que tomamos como ciertas porque sí.
Es decir, en matemática trabajamos con:
1.- Definimos unos objetos.
Números, vectores, funciones, conjuntos… llámalo X.
2.- Definimos unas afirmaciones que tomamos como ciertas.
A esto lo llamamos: AXIOMAS.
3.- Definimos unas reglas para manipular los objetos que hemos definido anteriormente.
4.- Haciendo uso de los objetos, las reglas definidas y los axiomas nos planteamos si una determinada afirmación que involucra dichos objetos es cierta o no dentro de este esquema.
Estas afirmaciones que se prueban como verdaderas dentro de este sistema los llamamos: TEOREMAS.
Y ESTOS TEOREMAS SON VERDAD ÚNICAMENTE DENTRO DEL ESQUEMA EN EL QUE SE HAN PROBADO COMO CIERTOS.
Al conjunto de puntos del 1 al 4 lo podemos llamar: SISTEMA FORMAL.
Por ejemplo, si yo digo:
Los ángulos de un triángulo suman 180º
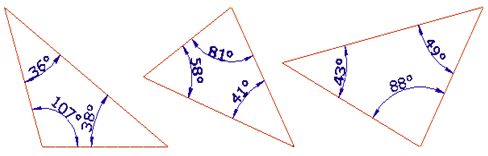
Esto es verdad en la geometría Euclídea.
Pero en una esfera, donde los axiomas de la geometría son diferentes a los de la geometría euclídea, esto no es cierto.

Aquí ya no estamos en la geometría euclídea sino en la geometría no-eclídea.
Por lo tanto, una cosa puede ser cierta en un sistema formal y falsa en otro.
Incompletitud

El caso es que Gödel dijo que en un sistema formal cerrado se podría dar el caso de poder formar una afirmación dentro de la que no podríamos decidir si era cierta o falsa.
En general, solemos pensar que si una afirmación no es cierta su negación sí lo es:
- Es falso que sea de noche, entonces es cierto que sea de día.
- Es cierto que llueve, entonces es falso que “no llueve”.
Sin embargo, en determinados sistemas formales no podemos probar que una afirmación o su negación sean ciertas o falsas dentro de dicho sistema.
Es decir, hay afirmaciones indecidibles.
Si encontramos una afirmación de este tipo en un sistema formal se dice que este es INCOMPLETO.
Claro, entonces como la matemática es un sistema formal esto implica que la matemática en incompleta y por tanto habrá cosas que no podamos demostrar.
FALSO.
Esta es la conclusión simplona que nos quieren vender del teorema de Gödel.
Gödel trabajó con la aritmética, y dijo que si esta era consistente, es decir, libre de contradicciones (que una afirmación y su negación fueran ciertas dentro de ella) entonces debería de ser incompleta (existirían afirmaciones indecidibles).
¿La matemática está condenada?
Pues no

.
¿Por qué?
Porque como el mismo Gödel demostró también existen sistemas formales completos. Todas las afirmaciones dentro de dicho sistema serán decibles.
Un ejemplo es el sistema de los números reales.
Y es curioso, porque los reales contienen a la aritmética de los naturales que no es completa.
El truco está en que nada nos prohíbe ampliar nuestro sistema formal, añadiendo nuevos axiomas, cambiando totalmente el conjunto de objetos, reglas y axiomas matemáticos o cualquier variante que se nos ocurra.
Así pues los matemáticos pueden trabajar tranquilos que si un teorema no se puede probar en una determinada rama de las matemáticas seguro que pueden recurrir a otra.
Valga como ejemplo que el señor Wiles demostró el último teorema de Fermat:

(que parece que es una relación entre números, y que con “aritmética” no se ha sabido demostrar. Es decir, no sabemos si es decidible o no en ese contexo.
utilizando curvas elípticas:
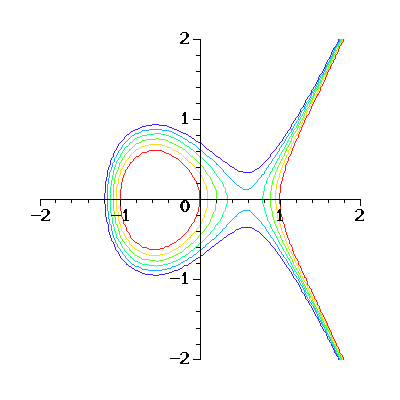
Entonces la física…
Entonces la física, nada. Es cierto que la física usa las matemáticas para expresar sus ideas y las teorías. Pero también es cierto que no está constreñida a usar aritmética.
Por tanto cuando nos dicen:
La física no puede probarlo todo por el teorema de Gödel.
Están cometiendo dos errores:
1.- La física no es un sistema formal cerrado.
2.- En física hay alguien que decide lo que es verdadero o falso en última instancia: EL EXPERIMENTO.
Aquí ahora podríamos discutir sobre si tendremos una teoría del todo, si esta teoría tendrá un conjunto de axiomas finitos y si estos son análogos a los de la aritmética. Entonces, podríamos discutir más en profundidad.
Por el momento hay que evitar confundir física con los modelos teóricos de la física y no hay que olvidar que es una ciencia experimental donde al final, la verdad o falsedad de un modelo se determina con observaciones y medidas.