domingo, 22 de diciembre de 2013

Ecuaciones de Maxwell y Relatividad (32430)

Qué tienen que ver las ecuaciones de Maxwell con la relatividad?
 En seguida vamos a verlo, pero, empecemos por el principio…
Maxwell
James Clerk Maxwell en una ilustración de 1880 aparecida en la revista Popular Science Monthly Volume 17
Las ecuaciones de Maxwell llevan más de 140 años describiendo los fenómenos electromagnéticos. Aquí las tenemos:
\vec{\nabla}\cdot \vec{E} = \dfrac{\rho}{\epsilon_0}
\vec{\nabla}\times \vec{B} = \mu_0 \vec{J} +\dfrac{1}{c^2} \dfrac{\partial \vec{E}}{\partial t}
\vec{\nabla}\cdot \vec{B} = 0
\vec{\nabla}\times \vec{E} = -\dfrac{\partial \vec{B}}{\partial t}
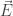donde \vec{E} es el campo eléctrico, 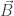\vec{B} es el campo magnético y 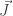\vec{J} la densidad de corriente.
Estas ecuaciones han resistido a todas las teorías de la Física que han venido después, incluida la relatividad. Esto significa que deberían poder aplicarse cuando tratemos con fenómenos relativistas.
Los fenómenos electromagnéticos son, en algunas ocasiones, curiosos. Por ejemplo, si tenemos un grupo de cargas fijas, un observador en reposo respecto a ellas ve un campo eléctrico asociado, pero otro observador que está en movimiento puede ver también un campo magnético. 
¿Cómo se pasa de una descripción a la otra? 
Necesitamos unas relaciones matemáticas que hagan las transformaciones .
 Y esas relaciones no son las conocidas transformaciones de Galileo, son las transformaciones de Lorentz.
Se llaman así porque en 1904 fueron escritas por Hendrik Antoon Lorentz.
 Las transformaciones proporcionaban una base para el desarrollo de la relatividad especial, aunque las consecuencias importantes de la relatividad no fueron descubiertas por este científico.
 Lorentz creía en el concepto de eter, e intentó ajustar sus cálculos para que cuadraran con dicho concepto.
Lorentz
Hendrick Antoon Lorentz por Jan Veth
Las transformaciones conectan las coordenadas del espacio y del tiempo de un sistema de referencia con las cantidades correspondientes en otro sistema de referencia que se encuentra en movimiento uniforme respecto al primero. Podemos interpretarlas como una rotación en el espacio de cuatro dimensiones 
x, y, z, t.
x' = \dfrac{1}{\sqrt{1-\dfrac{u^2}{c^2}}}\left( x - u t \right)
y' = y
z' = z
t' = \frac{1}{\sqrt{1-\dfrac{u^2}{c^2}}}\left( t - \dfrac{u}{c^2} t \right)
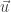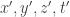donde \vec{u} es la velocidad uniforme de un sistema de referencia S’ que se mueve en la dirección x respecto de otro sistema de referencia S.  x',y',z',t' son las coordenadas en el sistema de referencia S’ y 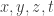x, y, z, t son las coordenadas en el sistema de referencia S.
Henri Poincaré y Albert Einstein enunciaron el principio de la relatividad, según el cual las leyes de la naturaleza deben ser las mismas para dos observadores en movimiento uniforme uno respecto al otro.
En concreto, en 1905, en su artículo “Sobre la electrodinámica de los cuerpos en movimiento” (en alemán, “Zur elektrodynamik bewegter körper”), Einstein enunció los dos postulados básicos de la relatividad.
卡西爱因斯坦Karsh Einstein
El primer postulado dice: “Las leyes de la naturaleza son las mismas en todos los sistemas de coordenadas que se mueven con movimiento uniforme uno respecto al otro”.
Y sabemos que los postulados de la relatividad especial tienen que cumplirse.
 Al menos, hasta ahora, todos los intentos de encontrar fisuras en esta teoría han fallado. Luego entonces, las ecuaciones de Maxwell tendrán que cumplir el primer postulado.  Y ¿lo hacen? Claro que sí. 
El propio Einstein en el mencionado artículo de 1905 lo comprueba.
Sin embargo, hemos visto que las transformaciones de Lorentz mezclan las coordenadas del espacio y del tiempo. En las ecuaciones de Maxwell las coordenadas deberían también aparecer en una forma simétrica. 
Dicho de otra manera, que entren en la ecuación en un nivel equivalente tanto coordenadas espaciales como el tiempo, con rotacionales y divergencias en cuatro dimensiones.
Hay una forma de escribir estas ecuaciones, llamada formulación covariante, en la que  tenemos esta simetría.  Serán las mismas ecuaciones, pero escritas de otro modo . Para llegar a esta formulación habrá que hacer algunas cuentas. Pues, allá vamos…
Sabemos que los campos eléctrico y magnético pueden derivarse de los potenciales escalar y vectorial, \phi y \vec{A}:
\vec{B} = \vec{\nabla}\times\vec{A}
\vec{E} = -\vec{\nabla}\cdot\phi - \dfrac{\partial\vec{A}}{\partial t}
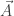Y con ambos potenciales vamos a escribir un cuadrivector 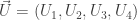\vec{U}=(U_1, U_2, U_3, U_4) donde:
U_1 = A_x
U_2 = A_y
U_3 = A_z
U_4 = \dfrac{i\phi}{c}
Al que vamos a llamar cuadripotencial o potencial universal.
Si calculamos las tres componentes del campo eléctrico y las tres del campo magnético, usando las definiciones anteriores, y sustituimos las componentes de los potenciales vector y escalar por las del potencial universal, obtenemos:
\frac{i}{c} E_1 = \dfrac{\partial U_1}{\partial x_4} - \dfrac{\partial U_4}{\partial x_1}
\frac{i}{c} E_2 = \dfrac{\partial U_2}{\partial x_4} - \dfrac{\partial U_4}{\partial x_2}
\frac{i}{c} E_3 = \dfrac{\partial U_3}{\partial x_4} - \dfrac{\partial U_4}{\partial x_3}
B_1 = \dfrac{\partial A_z}{\partial x_2}-\dfrac{\partial A_y}{\partial x_3}
B_2 = \dfrac{\partial A_x}{\partial x_3}-\dfrac{\partial A_z}{\partial x_1}
B_3 = \dfrac{\partial A_y}{\partial x_1}-\dfrac{\partial A_x}{\partial x_2}
Por tanto, 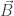\vec{B} e \dfrac{i}{c}\vec{E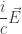} juntos, forman el rotacional cuadridimensional de \vec{U}.
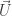Si ahora definimos una cantidad a la que vamos a llamar 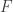F, Tensor de Campo Electromagnético, como:
F_{\mu\nu} = \dfrac{\partial U_{\nu}}{\partial x_{\mu}} - \dfrac{\partial U_{\mu}}{\partial x_{\nu}}
Resulta que 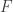F es el rotacional en cuatro dimensiones de \vec{U}.
F = \vec{\square}\times \vec{U}
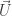¿Os gustan las matrices? Pues, vamos a escribir 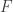F en forma matricial, simplemente, para verlo mejor:
F = \left( \begin{array}{cccc} 0 & B_3 & -B_2 & -\frac{i}{c}E_1 \\ -B_3 & 0 & _1 & -\frac{i}{c}E_2 \\ B_2 & -B_1 & 0 & -\frac{i}{c}E_3 \\ \frac{i}{c}E_1 & \frac{i}{c}E_2 & \frac{i}{c}E_3 & 0 \end{array} \right)
Ahora tenemos que calcular la divergencia del tensor de campo electromagnético. Nos queda lo siguiente.
\sum_{\nu=1}^{4} \dfrac{\partial F_{\mu\nu}}{\partial x_{\nu}} = \dfrac{\partial}{\partial x_{\mu}} \sum_{\nu} \dfrac{\partial U_{\nu}}{\partial x_{\nu}} - \sum_{\nu} \dfrac{\partial^2 U_{\mu}}{\partial x_{\nu}^2}
Y ahora, ¿qué hacemos con ésto? 
Aunque parece que las expresiones son cada vez más complicadas, en realidad, ya está casi todo el trabajo hecho. Vamos a ver que los dos sumandos a la derecha del igual van a simplificarse, de tal forma, que nos va a llevar a una fórmula muy sencilla para justo la  mitad de las ecuaciones de Maxwell.
El primer sumando es cero. Y ¿por qué? 
La respuesta está en una condición que hacemos cumplir a los potenciales escalar y vectorial, la llamada condición de Lorentz. 
Es ésta:
\vec{\nabla} \cdot \vec{A} = -\mu_0 \epsilon_0 \dfrac{\partial \phi}{\partial t}
Que escrita en función de las componentes del potencial universal es:
\sum_{i=1}^{4} \dfrac{\partial U_{\nu}}{\partial x_{\nu}} = 0
Hay una razón para imponer esta condicion y es simplificar las expresiones que se obtienen cuando en la segunda y cuarta ecuaciones de Maxwell sustituimos las ecuaciones que relacionan los campos con los potenciales.
 Operando, tras esta simplificación,  llegamos a una ecuación de onda para el potencial vector:
\nabla^2 \vec{A} - \frac{1}{c^2} \dfrac{\partial^2 \vec{A}}{\partial t^2} = -\mu_0 \vec{J}
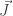Donde \vec{J} es la densidad de corriente.
Usando el cuadripotencial se escribe así:
\sum_{\nu=1}^{4} \dfrac{\partial^2 U_{\lambda}}{\partial x_{\nu}^2} = -\mu_0 J_{\lambda}
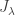donde J_{\lambda} son las componentes del cuadrivector 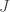J. Porque la densidad de corriente también puede, y debe, escribirse en forma covariante. 
 Las tres primeras componentes seran las componentes conocidas en tres dimensiones y la cuarta es ic\rho . Esto es así debido a la relación que existe entre ambas, la conocida ecuación de continuidad:
\vec{\nabla}\cdot \vec{J} + \dfrac{\partial \rho}{\partial t} = 0
Usando el cuadrivector se escribe:
\sum_{\nu=1}^{4} \dfrac{\partial J_\nu}{\partial x_\nu} = 0
O, lo que es lo mismo.
\vec{\square}\cdot \vec{J} = 0
Pero, no nos desviemos del camino. En la ecuación de onda del potencial vector escrita usando el cuadripotencial aparece, a la izquierda del igual, una expresión que vimos antes cuando calculamos la divergencia del tensor de campo electromagnético. 
Vamos a sustituir en la expresión de la divergencia del tensor esta expresión por lo que nos ha salido en la ecuación del potencial vector. Y nos encontramos, una vez hecho ésto, con una bonita expresión para 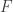F:
\sum_{\nu} \dfrac{\partial F_{\mu\nu}}{\partial x_{\nu}} = \mu_0 J_{\mu}
Pero a los físicos nos gustan más las ecuaciones simples y elegantes, así que la escribimos de esta manera:
\vec{\square}\cdot F = \mu_0 \vec{J}
Esta ecuación representa a las dos primeras ecuaciones de Maxwell, en lo que se llama Formulación Covariante de las Ecuaciones de Maxwell.
Las otras dos ecuaciones de Maxwell vienen representadas, en la mencionada formulación, por la siguiente expresión:
\dfrac{\partial F_{\mu\nu}}{\partial x_{\lambda}} + \dfrac{\partial F_{\nu\lambda}}{\partial x_{\mu}} + \dfrac{\partial F_{\lambda\mu}}{\partial x_{\nu}} = 0
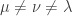donde \mu \neq \nu \neq \lambda representan tres de los subídices 1, 2, 3 ó 4. Esta formula se deduce directamente de la expresión del tensor de campo electromagnético.
Llegamos al final. 
Ahora, ya sabemos  cómo se escriben las ecuaciones de Maxwell para que las coordenadas del espacio y del tiempo estén tratadas a un nivel equivalente tal como se hace en relatividad.
¡Hasta pronto!
Publicado por en