La mecánica clásica era incapaz de explicar la existencia de átomos con protones y electrones ya que las cargas opuestas se atraen y, sin embargo, ambas partículas están separadas cuando forman átomos.
Era necesario explicar qué detenía a los electrones antes de llegar al núcleo.
En esta entrada veremos una posible forma de abordar el problema que además nos facilitará la conocida ecuación de la energía de Planck.
La energía electrostática:
Según la ley de Coulomb, la energía potencial creada entre 2 cargas q1 y q2 separadas una distancia r es:
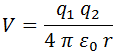
Aquí ε0 representa la permitividad del vacío. Básicamente esto implica que la energía tiende a cero cuando la distancia es infinita (cargas libres) y que la interacción será repulsiva si ambas tienen el mismo signo mientras que por el contrario será atractiva si tienen signo opuesto.
En principio esta energía definirá la interacción entre el núcleo y un electrón.
Extendiendo las unidades naturales:
La expresión anterior tiene en el denominador 3 términos de nulo interés físico, por lo que del mismo modo que omitimos previamente la velocidad de la luz y la constante de Planck para crear el sistema de unidades natural, en esta ocasión nos cargaremos la permitividad.
Para ello, en primer lugar tomamos su valor según el sistema internacional:
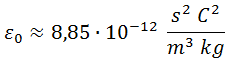
Tras esto, recordamos la equivalencia entre segundos y metros debida a la velocidad de la luz:
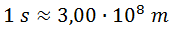
Y la equivalencia inversa entre quilogramos y metros debida a la constante de Planck:
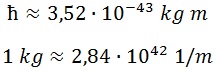
Teniendo esto, la permitividad en el sistema natural toma la forma:
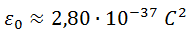
Y estamos interesados en imponer:
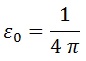
Con lo que, en resumen, estamos diciendo que el Coulombio deja de tener unidades y pasa a ser un número:

Sabiendo esto, podemos reescribir la carga del protón (opuesta a la del electrón) como:
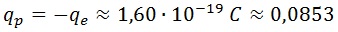
El truco que acabamos de hacer con las unidades da un valor numérico a la carga de los constituyentes del átomo que parece más “natural”, valga la redundancia, que cuando la expresamos en culombios.
Lagrangiana del sistema:
Como vimos ya en la entrada sobre el formalismo de Lagrange, la lagrangiana para una partícula girando en torno a otra con velocidad angular ω constante mientras es atraída por una fuerza central es:
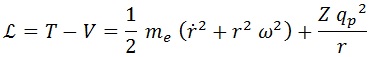
Aquí me es la masa del electrón y Z el número de protones en el núcleo (todos contribuyen a la carga).
El punto sobre la r representa una derivada temporal.
El movimiento queda determinado por las ecuaciones de Euler-Lagrange:
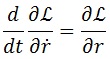

En principio esperamos que la órbita que describe el electrón sea circular, con lo que anulamos el término de la izquierda y fijamos la velocidad angular en función de la distancia:
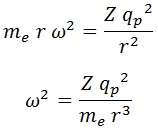
Sustituyendo todo esto en la lagrangiana para darle un valor numérico, obtenemos que su expresión final es:
Cuantización de la acción:
Como la lagrangiana es constante en el tiempo, sale fuera de la integral que define la acción. Lo que haremos para cuantizar el sistema (permitir que sus parámetros sólo tomen parámetros muy concretos) será: en primer lugar, recordar que la constante de Planck tiene unidades de acción; en segundo lugar, imponer que la acción cuando el electrón da una vuelta sea n veces un término proporcional a la constante de Planck.
Como dicha constante la estamos obviando, en resumen imponemos que la acción sea proporcional a un natural n:
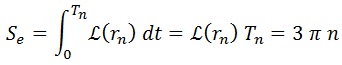
Cada valor de n fija un valor para la acción.
Según cuánto valga la acción el electrón estará a una distancia concreta rn y tendrá un periodo de giro Tn. Uno se podría preguntar por qué integramos en un periodo y por qué la constante al final es 3π.
La respuesta es “porque da”.
Decir que estamos haciendo algo sin sentido por fijar términos ad hoc no sería correcto. Esto simplemente va a ser un axioma para este movimiento, que ya es más que lo que teníamos.
Caracterización de átomos monoelectrónicos:
El periodo de giro es el perímetro de la circunferencia que recorre el electrón entre la velocidad con la que lo hace, que es a su vez el producto de radio por velocidad angular:

Teniendo esto y la lagrangiana, podemos sustituir en la igualdad que obtuvimos cuantizando la acción para obtener una expresión para el radio del átomo en función de n:

Vemos que cuanto mayor es la acción mayor es el radio, de modo que el radio más pequeño posible tiene n igual a la unidad.
Por otra parte, vemos que el radio disminuye cuantos más protones hay debido a que la atracción electromagnética es más fuerte.
Además, si quisiésemos considerar que la partícula de carga negativa que oscila en torno al núcleo no es un electrón sino alguno de sus hermanos de masa mayor, como el muón o el tauón, también quedarían más cerca.
Antes de dar un valor numérico a la masa es importante recordar la correspondencia natural entre electronvoltios (eV), julios (J) y quilogramos:
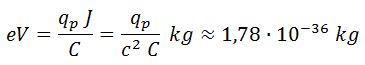
Consecuentemente, la masa del electrón en quilogramos, electronvoltios y metros es:
Lo que nos da un radio de la forma:
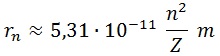
Cuando tenemos un protón y el nivel energético fundamental, el electrón está a 53,1 picometros del núcleo, distancia conocida como radio de Bohr y que define al átomo de hidrógeno más elemental.
La velocidad angular resultante implica una cantidad enorme de revoluciones por segundo, aumentando con el número de protones y disminuyendo con la energía:

Por su parte, la velocidad es muy pequeña comparada con la de la luz siempre que el nivel energético no se dispare, con lo que no debemos preocuparnos por no haber analizado el problema de forma relativista:
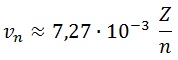
La expresión para la energía, que llevamos todo el rato diciendo que aumentará con n, toma la forma:
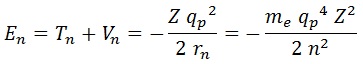
Nótese que aunque n aparezca dividiendo, como la energía es negativa realmente aumenta. Numéricamente, vemos que un átomo pequeño supone una inversión energética del orden de las decenas de electronvoltios:
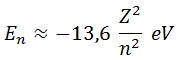
En otras entradas analizaremos en más detalle la cuantización en átomos.
La energía de Planck:
Para concluir, podemos repetir rápidamente este planteamiento con un rayo de luz propagándose con periodo T.
Como no interacciona con nada, su energía potencial es nula y su lagrangiana, su energía cinética y su energía son idénticas:
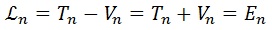
Al imponer la cuantización sobre su acción obtenemos directamente que la energía es la frecuencia (multiplicada por la constante de Planck).
En este caso elegimos como factor de proporcionalidad 2π:
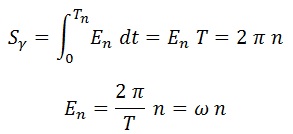
La energía de un haz de luz de periodo/frecuencia característica es una composición de n paquetes de energía, fotones γ, de valor idéntico a la frecuencia en unidades naturales.
Conclusiones:
Tenemos una forma de fijar valores de la acción que reproduce las cosas bien, aunque no resulta intelectualmente muy satisfactoria porque simplemente da. Tenemos también que la constante de Planck es fundamental para obtener valores correctos en el orden de magnitud esperable.
Si bien es evidente que esta no es una teoría última de la física, sí que obtenemos 2 cosas muy importantes: la acción va a ser la suma de n cosas contribuyendo siempre y cualquier sistema cuántico debe imponer de algún modo los valores que permite para sus parámetros.