Una entrada anterior ha suscitado cierta polémica sobre si un determinado efecto era clásico o cuántico. Si el uso de la cuántica no era más que un capricho.
La sensación que me ha dado la discusión, y esto es una apreciación personal, es que hay ciertas reticencias a que la cuántica sea la que marque las normas.
No entiendo el porqué. La cuántica ha superado todas las pruebas experimentales durante su siglo (aproximadamente) de existencia.
Y aquí deberíamos insistir en que los experimentos se diseñan generalmente para mostrar que la cuántica se equivoca.
Y hasta el momento nadie ha conseguido un resultado positivo en este sentido.
Por eso quiero dedicar unas cuantas líneas a aclarar ciertas confusiones que pueden generarse con estos ejemplos experimentales o con las discusiones que se presentan a la luz de los mismos.
Y para que conste… A mí los clásicos me encantan.

¿La clásica y la cuántica explican los mismos fenómenos?
Pues evidentemente no, la clásica no puede explicar la estabilidad de la materia, por poner un ejemplo. La cuántica y la clásica se diferencian en muchas de sus predicciones en muchos fenómenos, desde el efecto fotoeléctrico hasta el efecto túnel.
Ahora bien, hay situaciones en las que la cuántica y la clásica tienen que dar necesariamente los mismos resultados.
Es por aquello de que la física clásica no es más que un límite de la cuántica.
Es decir, la física clásica emerge de la cuántica en determinados límites.
¿Cuáles son los límites esos?
1.- Que se involucren muchas partículas.
2.- Que las energías sean altas comparadas con la constante de Planck.
3.- Que las condiciones experimentales no excluyan una de las dos opciones (clásica/cuántica).
Evidentemente hay muchos matices a estas condiciones pero esencialmente podemos decir que se cumplen en las situaciones usuales.
Por lo tanto, si uno tiene una onda electromagnética podría hacer la descripción como onda clásica o como un paquete de miles de millones de fotones. Personalmente me decantaría por la primera opción, por aquello de simplificar los cálculos y tal.
En la entrada en cuestión, se ha discutido sobre si el resultado experimental ese es propio de la cuántica o de la clásica.
La respuesta es que se puede estudiar con ambas teorías.
Pero hay un matiz importante del que nos vamos a ocupara después de hablar de un ejemplo que nos va a esclarecer el tema.
Cuando todo se reduce a un fotón

Viñeta de Nick Kim
Aproximadamente desde mediados de los años 80 del pasado siglo somos capaces de hacer experimentos con un único fotón.
No entraremos aquí en los detalles técnicos de esto. Ya le dedicaremos otra entrada a cómo se consigue aislar un único fotón. Pero para los interesados:
Bien, nos guardamos en la cabeza que es posible experimentar con un único fotón.
Ahora hablaremos de otro elemento que nos va a ser útil.
El divisor de haz.
Divisor de haz
Un divisor de haz es un cristal que tiene la particularidad de que cuando le llega un flujo de luz divide la intensidad en dos direcciones perpendiculares. La mitad de la luz es reflejada y la otra es transmitida.

1 –> Haz incidente 2 –> Haz transmitido (50% del incidente) 3 –> Haz reflejado (50% del incidente)

Divisores de haz
Pues bien, ¿qué pasa si lo que lanzamos al divisor de haz es un único fotón?
Según la clásica, cualquier onda electromagnética se dividiría en dos partes con una reducción de intensidad a la salida. Si pusiéramos detectores en las dos direcciones de salida dichos detectores tendrían que dar señal simultáneamente. Evidentemente les llegarían ondas a la vez y serían detectadas.
Pero si reducimos la onda electromagnética a un único fotón, cosa que es posible, tenemos una situación nueva.

En este caso lo que se encuentra experimentalmente es lo siguiente:
1.- Si uno de los detectores se activa (detecta el fotón) el otro no lo hace.
2.- Si repetimos el experimento en las mismas condiciones muchas veces, el 50% de las veces el fotón llegará a un detector y el 50% de las veces llegará al otro.
3.- Nunca hay una detección simultánea de ambos detectores a la vez.
Esto se ha comprobado experimentalmente en muchas ocasiones, entre ellas en este artículo:
Este ejemplo indica que hay situaciones en los que la clásica no puede explicar ciertos fenómenos “sencillos”. A menos que pensemos que la clásica puede concluir que el fotón elige un único camino en cada caso… Y que en cada repetición se decide por un camino u otro con una probabilidad del 50%.Una idea peregrina, pero alguien podría pensar así.
Así que tendremos que ir a otro caso un poco más complicado.
Compliquemos la cosa
Ahora vamos a jugar con dos divisores de haz y dos espejos dispuestos de la siguiente manera
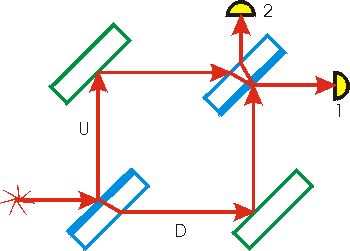
Los divisores de haz están en azul.
Los espejos están en verde.
A esta configuración se la denomina interferómetro de Mach-Zehnder.
En la misma uno puede ajustar las posiciones de los espejos (que reflejan toda la luz recibida, al contrario que los divisores de haz) para hacer los caminos recorridos por los haces divididos más largos o más cortos.
Si fijamos una configuración estaremos provocando una interferencia a la salida del interferometro.
Eso quiere decir que tendremos zonas por las que nunca detectaremos luz y otras en las que detectaremos toda la intensidad.
Evidentemente si estamos jugando con muchos fotones las predicciones de la cuántica y la clásica coinciden. El proceso es una interferencia, y ambas teorías nos dirán donde podremos o no detectar la luz que ha interferido.
Ahora tomemos un único fotón, y lancémoslo sobre el interferómetro con una configuración de espejos que nos dice que siempre irá a parar a uno de los detectores. (Esto es perfectamente posible, solo hay que usar la interferencia).

Esto equivale a decir que hemos conseguido una interferencia destructiva en uno de los detectores y una interferencia constructiva en el otro.
Aquí nos enfrentamos a varias cuestiones siendo las más importantes:
¿Cómo es posible que el fotón que se detecta como partícula interfiera como onda? ¿Un único fotón? ¿Un único fotón en el sistema es capaz de producir interferencias? ¿No se detectaba cada vez por un camino en el caso anterior?
Si le preguntamos a la clásica nos dirá que el fotón es como una onda y ha pasado por los dos caminos a la vez para poder interferir.
Pero ojo, eso es incompatible con la idea del otro experimento en el que en cada ocasión se decanta por un camino o por otro.
Pues bien, la cuántica (como se puede comprobar en los artículos enlazados previamente en esta entrada) explica esto sin problemas, lo asume como natural ya que combina información de partícula y de onda en un único sistema cuántico.
¿Qué problema tenía la controvertida entrada?
En la entrada, se dio lugar una interesante discusión. En lo tratado en esta entrada se ponía de manifiesto un fenómeno cuántico en esencia. Sin embargo, se puede deducir de forma clásica.
¿Por qué dije que era un fenómeno cuántico?
a) Porque el fenómeno tiene su raíz en la interferencia cuántica de fotones individuales. Pero en el experimento realizado se trabajan con muestras que contienen del orden de  fotones.
fotones.
b) Es cierto que tal y como está diseñado el experimento todo lo que importa es el carácter ondulatorio de las partículas tratadas, de hecho son tantas que la aproximación por onda electromagnética clásica es pertinente.
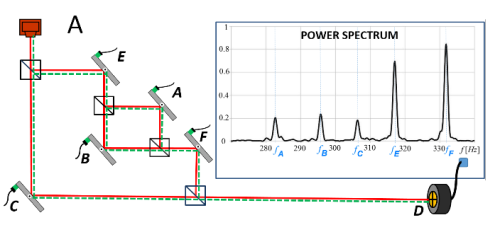
La configuración del experimento es esa. Hay varios interferómetros MZ anidados. El problema aquí es que solo hay un detector ya que toda la señal se condensa al final para dirigirla al mismo, por tanto la aproximación clásica es válida. ¿Por qué?
Porque no hay posibilidad de preguntarle al sistema por características ondulatorias y corpusculares al mismo tiempo. Sin embargo…
¿Qué pasaría si se repitiera este experimento con un único fotón?
¿Qué resultado obtendríamos? ¿La descripción clásica sería válida?
Afortunadamente estoy convencido de que este tipo de experimentos se repetirán con fotones aislados, con neutrones y con otros sistemas cuánticos de forma que la explicación clásica no sea aplicable.
En el artículo sobre el que iba la entrada anterior lo único que han puesto de manifiesto es:
1.- El experimento es realizable. Ahora hay que mejorarlo.
2.- El resultado del mismo lo puede explicar la cuántica y es más fácil de “visualizarlo” con una determinada formulación.
3.- Se seguirá trabajando en esta línea para explorar estos resultados en distintos sistemas.
Y a modo de final… La cuántica es imprescindible para entender nuestro universo y supera a la clásica en la explicación de muchos fenómenos.
Nos seguimos leyendo…