miércoles, 18 de diciembre de 2013

Oscilones (32328)

El Hamiltoniano


Como hemos explicado el Hamiltoniano del oscilador armónico se puede escribir como:
\hat{H}=\hbar\omega(a^\dagger a+\dfrac{1}{2})
En el Reto II hemos demostrado que esta forma del Hamiltoniano es equivalente a la forma usual en términos de energías cinéticas y potenciales. 
 Y además hemos visto que para que la teoría sea consistente se ha de cumplir:
[a,a^\dagger]=1
Lo que implica la condición básica de la mecánica cuántica entre posiciones y momentos:
[\hat{x},\hat{p}]=i\hbar
Ahora nos proponemos a ver para qué sirven esto y de qué manera podemos interpretar los objetos a y a^\dagger.

Número

Dado que el Hamiltoniano tiene la forma \hat{H}=\hbar\omega(a^\dagger a +\dfrac{1}{2}) uno puede dar un nombre a la asociación a^\dagger a. 
 A esta asociación la llamaremos operador número (la razón se hará evidente en lo que sigue) y lo denotaremos por \hat{N}. 
 Por lo tanto el operador número es:
\hat{N}=a^\dagger a
Y así el Hamiltoniano se puede escribir cómo:
\hat{H}=\hbar\omega(\hat{N}+\dfrac{1}{2})
Calculemos unos cuantos conmutadores.  
Recordemos que el conmutador es la operación esencial en la mecánica cuántica, esta operación es la que determina las particularidades de la teoría, así que siempre es interesante jugar con estos bichos.
Dado que ya hemos calculado varias veces conmutadores en esta ocasión los dejaremos sin desarrollar poniendo simplemente los resultados finales. 
 Conmutadores varios:
1.-  [\hat{N},\hat{H}]=0
2.- [\hat{N},a]=-a
3.- [\hat{N},a^\dagger]=+a^\dagger
4.- [\hat{H},a]=-\hbar\omega a
5.- [\hat{H},a^\dagger]=+\hbar\omega a^\dagger
La ecuación de Schrödinger en abstracto. Notación de Dirac
Como hemos discutido varias veces a lo largo del blog la ecuación de Schrödinger (independiente del tiempo) se escribe cómo:
\hat{H}\psi_n(x)=E_n\psi_n(x)
Aquí estamos viendo el estado cuántico expresado en función de las coordenadas espaciales, al ser este ejemplo de una dimensión sólo depende de x.  
Pero también podemos expresarlo en términos del momento, p. 
 O bien podríamos buscar otras combinaciones siempre y cuando se respeten la condición
 [\hat{x},\hat{p}]=i\hbar.
Pero eso sólo es una forma de representar los estado, en realidad el estado cuántico no tiene por qué ser expresado en términos de posiciones, momentos u otras variables. 
 En mecánica cuántica el estado es un objeto abstracto que contiene toda la información que podemos obtener del sistema descrito, y ese objeto abstracto viene representado por |\psi\rangle. 
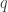 Si este objeto, que llamaremos estado, se entiende como una función de las coordenadas lo escribiremos \psi(x), si lo consideramos como función de los momentos \psi(p) y si es en una coordenada arbitraría q definida como sea pero consistente con la teoría, \psi(q).
Por lo tanto uno puede escribir la ecuación de Schrödinger en este caso como:
\hat{H}|\psi_n\rangle=E_n|\psi_n\rangle
Aquí |\psi_n\rangle  Es el estado del sistema que tiene una energía dada por E_n.  En el caso del oscilador armónico E_n=\hbar\omega (n+\frac{1}{2}).
Estos estados se llaman estados propios del Hamiltoniano o autoestados del Hamiltoniano. 
 Y son estados en los que el sistema tiene una energía definida.
Sin embargo, podemos preguntarnos que le pasa a un estado |\psi_n\rangle cuando le aplicamos los objetos a o a^\dagger.  Con esto veremos cómo interpretar estos objetos y ponerles, por fin, un nombre adecuado.

Creación y Aniquilación


Bien, nosotros sabemos que tenemos una clase de estados |\psi_n\rangle que tienen la particularidad de tener una energía definida. 
 Es decir, cuando les aplicamos el Hamiltoniano nos dice que tienen una energía E_n.
Ahora nos preguntamos:
¿Qué les hace el objeto (operador) a a los estados |\psi_n\rangle?
¿Tendrá una energía definida o no?
Estudiaremos el procedimiento pormenorizadamente:
1.-  Aplicamos el operador a en un estado |\psi_n\rangle.
a|\psi_n\rangle
En principio, no tenemos ni idea del resultado.
  Lo que podemos suponer es que al actuar a sobre el estado |\psi_n\rangle
 lo cambia a un estado |\chi\rangle.
|\chi\rangle=a|\psi_n\rangle
Pero queremos saber si tiene energía definida o no, entonces vamos a aplicar a ese estado el Hamiltoniano.
\hat{H}|\chi\rangle=\hat{H}(a|\psi_n\rangle)=\hat{H}a|\psi_n\rangle
2.-  Lo que sabemos cómo actúa sobre el estado de energía definida es el Hamiltoniano, así que en vez de tener \hat{H}a nos gustaría tener la agrupación a\hat{H}.   Pero no podemos darle simplemente la vuelta porque como hemos visto antes no conmutan, así que lo que podemos usar es el conmutador:
[\hat{H},a]=-\hbar\omega a
y [\hat{H},a]=\hat{H}a-a\hat{H}
Por lo tanto,
\hat{H}a=a\hat{H}+[\hat{H},a]=a\hat{H}-\hbar\omega a
3.-  Ahora lo que podemos hacer es lo siguiente:
\hat{H}a|\psi_n\rangle=(a\hat{H}-\hbar\omega a)|\psi_n\rangle
Eso se puede escribir:
a\hat{H}|\psi_n\rangle-\hbar\omega a|\psi_n\rangle
4.-  Lo que ahora sabemos es como actúa el Hamiltoniano sobre el estado, por lo tanto:
aE_n|\psi_n\rangle-\hbar\omega a|\psi_n\rangle=
=(E_n-\hbar\omega)a|\psi_n\rangle
5.-  Recordemos que E_n=\hbar\omega (n+\frac{1}{2}) por lo tanto:
E_n-\hbar\omega=\hbar\omega\left((n-1)-\dfrac{1}{2}\right)
Pero eso es la energía E_{n-1}.
6.- Por lo tanto, cuando aplicamos el Hamiltoniano al estado |\chi\rangle=a|\psi_n\rangle lo que nos dice es que tiene la energía E_{n-1} y por tanto podemos decir que |\chi\rangle=|\psi_{n-1}\rangle.
Entonces la actuación de a  sobre el estado |\psi_n\rangle baja destruye un cuanto de energía y nos da el estado |\psi_{n-1}\rangle. 
 Por eso se llamaremos a a operador de destrucción.
Ahora podéis intentar mostrar por qué a^\dagger se llama operador de creación.  
Espero que lleguen a que a^\dagger|\psi_n\rangle
 nos da |\psi_{n+1}\rangle.

Oscilones


En este contexto la única característica intrínseca que podemos saber del sistema es su energía.  Y hemos visto que con a^\dagger y a aumentamos o disminuimos un cuanto de energía del oscilador.
Si pensamos que eso es porque aparecen partículas con una energía dada, lo que nos está diciendo es que estamos creando o destruyendo partículas con una energía \hbar\omega y les podríamos poner  por ejemplo oscilones.
En teoría cuántica de campos, ocurre esto justamente, cuando uno estudia el campo electromagnético encuentra que hay excitaciones del campo que se pueden crear y destruir (con operadores a^\dagger y a). 
 Y a estas excitaciones se les llama fotones. 
 La situación es la misma en todos los campos.

Operador Número otra vez


Si ahora hablamos en términos de oscilones, partículas cuánticas del oscilador, podemos hablar de:
1.-  El vacío |\psi_0\rangle es el estado de mínima energía:
\hat{H}|\psi_0\rangle=E_0|\psi_o\rangle
Este estado tiene una energía correspondiente a n=0:  E_0=\dfrac{1}{2}\hbar\omega.
Dado que es el vacío, no hay oscilones, si aplicamos el operador de destrucción sobre el vacío simplemente nos devuelve un 0, no hay nada que destruir:
a|\psi_0\rangle=0
Esta es la propiedad que define al estado de vacío. 
 El vacío es aquel estado que está aniquilado totalmente por el operador de destrucción.
Uno puede tomar otra representación para el estado, |o\rangle representa al estado sin partículas, el vacío.
Apliquemos el operador número sobre este estado representado de este modo:
\hat{N}|0\rangle=a^\dagger a|0\rangle
Dado que el operador de destrucción aniquila el vacío lo mejor es darle la vuelta a la agrupación a^\dagger a empleando el conmutador:
=(aa^\dagger - [a,a^\dagger])|0\rangle=(aa^\dagger-1)|o\rangle
Entonces tenemos:
=aa^\dagger|0\rangle-|0\rangle
Como a^\dagger crea un estado con un oscilón más diremos:
a^\dagger|0\rangle=|1\rangle
Por lo tanto:
=a|1\rangle -|0\rangle
La actuación del operador de destrucción es un poco más “elaborada”, aunque no lo demostraremos en esta entrada, diremos que en la notación de número de partículas el operador de destrucción actúa así:  a|n\rangle=n|n-1\rangle.  
Así en este caso tenemos:
=|0\rangle-|0\rangle= (1-1)|o\rangle=0|0\rangle
Y por tanto \hat{N}|0\rangle=o|0\rangle, es decir que nos dice cuantas “partículas” tenemos en el sistema.  Por partículas entendemos excitaciones del sistema con particularidades como masa, carga, espín, etc. 
 En este caso lo único que las identifica es la energía, pero la idea es la misma en situaciones más complicadas.
¿Podemos demostrar que \hat{N}|3\rangle=3|3\rangle?
Esto nos permite emplear la notación |n\rangle para decir que es un oscilador con energía E_n lo cual se puede entender como que tenemos n excitaciones, partículas, oscilones como nos hemos empeñado en llamar.

Una última pregunta


Aunque no hemos hablado del tema del espín de estos oscilones, me gustaría preguntar algo:
¿Creen que estas partículas serán bosones o fermiones? ¿Por qué?
Esperamos que les haya gustado esta entrada.
Lo que quiero mostrar es que es algo asequible si se le dedica tiempo y ganas y que no es algo para sólo unos pocos.  Está claro que esto es lo más básico y que las cosas se pueden poner muy feas  desde el punto de vista matemático, pero la base y el fundamento de todo se puede centrar en esto que estamos discutiendo.
 La idea es seguir con esta línea hasta presentar supersimetría en este sistema simple del oscilador armónico.   Y luego, cuando leamos divulgación disfrutaremos sabiendo que cuando nos dicen que en cuántica aparecen y desaparecen nosotros ya sabemos por qué y cómo.
Nos seguimos leyendo…
Publicado por en