Cuando nos ponemos a hablar de Ciencia en relación a su historia y los orígenes de la misma, la mayoría de las veces nos perdemos por vericuetos que nos llevan, hasta callejones sin salida, situados muy lejos en el tiempo y que no podemos ver con claridad. Así las cosas, estamos obligados a ser menos ambiciosos y mirar más cerca poder obtener algunos resultados más fiables de lo que pudo pasar en esos pueblos del mundo que, como Sumer, India, Egipto, China y más tarde Grecia, nos dejaron una buena colección de señales del saber que pudieron llegar hasta nuestros días. De todo eso hemos hablado aquí en los últimos trabajos presentados.

La ciencia y el pensamiento proceden de la necesidad de investigar, de indagar, y su fin es la investigación.
Ésta nace de una insatisfacción frente a las respuestas que proporciona la tradición las preguntas fundamentales de la existencia humana y material.
El fundamento de la primera ciencia de que se tiene noticia, la filosofía, consiste en que el hombre no posee las respuestas a las cuestiones que se le plantean, sino que debe buscarlas para alcanzar la sabiduría: no es “sophias” (sofía) o sabiduría en sí, sino “philosophia”, es decir, amor por la sabiduría, deseo de poseer la sabiduría, indagación directa para rastrear la verdad más allá de las costumbres, de las tradiciones y de las apariencias.
Se han realizado algunos estudios en los que, finalmente, se reconocía que entre el siglo IX y el siglo XV “el flujo de la ciencia y la tecnología entró en Europa sobre todo procedente del Islam”. Expertos de la Revista Sciencie informa de que las contribuciones del Islam y de China figuran entre los acontecimientos que “representan los innumerables giros, vueltas, paradojas, contradicciones, tragedias y otros detalles históricos deshilvanados que se han sintetizado en esa realidad mucho más compleja y variada que es la aventura científica”.
Otros acontecimientos de este que figuran en la lista son la práctica de la Alquimia por parte de Newton, el falso descubrimiento de los “rayos N” y las negativas de los geólogos a aceptar la teoría de la deriva continental.

Por lo general, cuando oímos hablar de Isaac Newton nos vienen a la cabeza sus aportaciones a la ciencia, y en especial a la física y las matemáticas.
Sin embargo, Newton no sólo fue uno de los más importantes científicos de todos los tiempos, sino que a lo largo de su vida dedicó gran de sus esfuerzos a cuestiones como la Alquimia o la teología, interesándose, por ejemplo, en descifrar lo que interpretó como un código oculto en la Biblia –lo que le llevó al estudio de la cábala hebrea–, o en intentar determinar el probable aspecto del Templo de Salomón, además de muchas otros intereses que hoy pueden resultarnos insólitos un científico.
No existe una buena definición de la Ciencia. Después de muchas tentativas, la American Physical Society, se decidió finalmente por una definición pero, consideraba que si la definición era muy larga, se podrían colar en ella alguna pseudociencias tales como ; si la hacían demasiado estricta, podrían quedar excluidos temas como la teoría de cuerdas, la biología evolutiva e incluso la Astronomía.

Es una Ciencia por derecho propio, nos habla del Universo, del espacio-tiempo, de todo lo que existe y que está conformado por la materia y, de las fuerzas que lo rigen todo. Así que definir lo que la Ciencia es, ser realistas, no es una tarea fácil si tenemos en su diversidad, su complejidad, su maravillosa y extensa estructura que hace un recorrido que abarca todo el saber del mundo y, sintetizar eso, en unas pocas palabras…aparte de ser una difícil tarea, tiene el peligro de no decir lo que pretende expresar.
“La ciencia es un estudio lógico y sistemático de la naturaleza y del mundo físico que, generalmente incluye tanto experimento como teoría”.
En verdad es una definición bastante floja. La Ciencia, es mucho más que eso y, para esa incompletitud, mejor me quedaría con: “La Ciencia es la que nos lleva hacia la Sabiduría, hacia el conocimiento del “mundo”, del Universo y todo lo que en él está presente”.

Todo evoluciona y nada permanece, los cambios son irreversibles
En la primera definición (no la mía), el autor ha puesto generalmente en cursiva, y explica:
“porque si planteáramos una exigencia absoluta de experimentos, tendríamos que excluir la Astronomía, la más antigua de todas las ciencias, ya que no es posible recrear nuevas estrellas o galaxias en el laboratorio, ni escenificar la formación del Sistema solar. Sin embargo, en astronomía las observaciones son a menudo tan valiosas como el experimento. El cometa Halley regresa con una regularidad sorprende; el Sol sale mañana”.

El Filósofo Kal Popper añadió el requisito de la “refutación”.
La Ciencia es refutable; la religión no es. Una teoría o una ley científica nunca pueden ser demostradas de una manera absoluta; de ahí que sea posible refutarlas. Por ejemplo,
( F= ma).
No podemos demostrar que todos los objetos de todas las galaxias obedecen esta ley o que todos los objetos obedecerán siempre esta ley.
Sin embargo, demostrar la falsedad de esta ley bastaría un sólo experimento. (Albert Einstein y algunos expertos en física cuántica han demostrado que algunos de los conceptos de Newton son erróneos).
Por lo tanto, los científicos deben proponer sólo teorías que puedan ser refutadas, tal afirmó Popper.
Estas teorías han de ser comprobables.
No existe tal requisito en el caso de la religión.

Dicho esto, sigue habiendo problemas con la definición de lo que la Ciencia es. , por ejemplo, es refutable. Si un astrólogo nos dice que nos encontraremos con una guapa extranjera el martes, esto puede comprobarse.
Por otra parte, la teoría de las supercuerdas, planteada por algunos físicos como la “teoría de todo”, requeriría un acelerador de partículas de diez años-luz de diámetro para poder refutarla.
La mayor parte de la biología evolutiva tampoco puede comprobarse experimentalmente. No se puede reproducir la evolución de una nueva especie, ni recrear los dinosaurios comenzando con un animal unicelular.
Si aplicamos la regla de la refutación demasiado estrictamente, tendremos que incluir la astrología en el campo de la ciencia y excluir la biología evolutiva, la teoría de cuerdas y quizá incluso la astronomía.

En consecuencia, es mejor que no nos tomemos demasiado en serio lo de la refutación de Popper. De otro modo, podríamos vernos obligados a excluir toda la ciencia de los antiguos griegos.
Éstos no sólo eludían los experimentos, sino que abominaban de ellos, confiando en que la razón estaba por encima de la evidencia empírica.
Algo que no se debe tomar en consideración es el pragmatismo de la ciencia o la motivación del científico.
Estas cuestiones se han utilizado a menudo desacreditar las ciencias no occidentales: sí, es un bien hecho , pero no es “puro”; o, a la inversa, no resulta práctico.En cuanto a la motivación, muchos descubrimientos científicos fueron impulsados por motivos religiosos: los matemáticos árabes perfeccionaron el álgebra en para facilitar las leyes islámicas de la herencia, del mismo modo que los védicos de la India resolvieron raíces cuadradas para construir los altares de los sacrificios con unas dimensiones adecuadas.
En estos casos, la ciencia estuvo al servicio de la religión.

La ley de los opónimos de Stigler, formulada por el experto en estadística Stephen Stigler (arriba), afirma que ningún descubrimiento científico lleva el de su descubridor original. Él mismo admite que “su Ley”, en realidad, fue descubierta por Robert K. Merton, un especialista en sociología de la ciencia.
Entre todos los casos en los que se cumple la Ley Stigler, el más famoso es el del Teorema de Pitágoras, según el cual la suma de los cuadrados de los dos lados perpendiculares de un triángulo rectángulo es igual al cuadrado de la hipotenusa de dicho triángulo. O bien en lenguaje matemático, a2 + b2 = c2, donde a y b son los lados perpendiculares y c es la hipotenusa. Jacob Bronowski escribe lo siguiente:

“Hasta la , el Teorema de Pitágoras sigue siendo el teorema más importante de todas las matemáticas. Esta afirmación puede parecer atrevida y extraordinaria, pero no es extravagante, ya que lo que el teorema de Pitágoras establece es una caracterización fundamental del espacio en que nos movemos y es en este teorema donde dicha caracterización se expresa por primera vez traducida a números. Además, el encaje exacto de los números describe las leyes exactas que rigen el universo. De hecho, se ha propuesto que los números correspondientes a las dimensiones de los triángulos rectángulos sean mensajes que podrían enviarse a planetas de otros sistemas solares a modo de test, comprobar si en estos planetas existe vida racional”.

Claro que, los hindúes, los egipcios y los babilonios utilizaban “tríos pitágóricos”determinar ángulos rectos en la construcción de edificios. Un trío de números pitagóricos es un conjunto de tres números que representan las dimensiones de los lados de un triángulo rectángulo. Pitágoras “inventó” su teorema hacia el año 550 a. C. Los babilonios habían catalogados cientos de tríos antes del año 2000 a. C., en una época en la que Pitágoras ni había nacido.
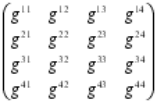
Lo mismo se podría decir de Riemann y Einstein, cuando éste último utilizó el Tensor métrico de aquel (formulado 60 años antes) poder formular su teoría de la relatividad general. Riemann creó su tensor métrico que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2.
El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él.
Claro que, es una herramienta para utilizar en un mundo tridimensional).

Los espacios curvos de Riemann
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Eintein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la realtivdad general.
La reinterpretación física de la famosa conferencia de Riemann se denomina relatividad general, y las ecuaciones de campo de Einstein se sitúan las ideas más profundas de la historia de la ciencia.

Sí, dudas hemos tenido todos
Hay otras muchas cuestiones de las que podríamos hablar y, la Física y la Astronomía, siendo mi gran Pasión, ocupa mucho de mi tiempo
- Una simetría unificadora.
- La capacidad de explicar grandes cantidades de experimentales con las expresiones matemáticas más económicas.
El Modelo Estándar falla en ambos aspectos, mientras que la relatividad general los exhibe, ambos, de manera bien patente. Nunca una teoría dijo tanto con tan poco; su sencillez es asombrosa y su profundidad increíble.
De hecho, que se publicó en 1.915, no ha dejado de dar frutas, y aún no se han obtenido de ella todos los mensajes que contiene.
El principio director del modelo estándar dicta que sus ecuaciones son simétricas. De igual modo que una esfera ofrece el mismo aspecto desde cualquier punto de vista, las ecuaciones del modelo estándar subsisten sin variación al cambiar la perspectiva desde la que son definidas.
Las ecuaciones permanecen invariables, además, cuando esta perspectiva se desplaza en distinta magnitud a diferentes puntos del espacio y el tiempo.

Al contrario de la relatividad general, la simetría del Modelo Estándar, está realmente formada empalmando tres simetrías más pequeñas, una por cada una de las fuerzas; el modelo es espeso e incómodo en su .
Ciertamente no es económica en modo alguno. Por ejemplo, las ecuaciones de Einstein, escritas en su totalidad, sólo ocupan unos centímetros y ni siquiera llenaría una línea de esta página. A partir de esta escasa línea de ecuaciones, podemos ir más allá de las leyes de Newton y derivar la distorsión del espacio, el Big Bang y otros fenómenos astronómicos importantes como los Agujeros Negros. Por el contrario, sólo escribir el Modelo Estándar en su totalidad requeriría, siendo escueto, un par de páginas y parecería un galimatías de símbolos complejos sólo entendibles por expertos.
Claro que, todo esto es, otra historia.
Universo.org.es
Universo.org.es