domingo, 9 de febrero de 2014

Cafè matemàtico: La fórmula del binomio (33017)

Foto: Cafè matemàtico: La fórmula del binomio (33017) entrada completa en alquimiayciencias.blogspot.com.ar

 Teorema. 
Si a,b \in \mathbb{R} son números reales y n \in \mathbb{N} es un número natural entonces se tiene la identidad
\displaystyle{(a+b)^n = \sum_{k=0}^n \left ( \hskip -1ex\begin{array}{c} n \\ k \end{array}\hskip -1ex \right ) a^{n-k}\,b^k.}
Demostración. 

 Razonamos por inducción matemática. 

La identidad es trivial cuando n=1 puesto que


\displaystyle{(a+b)^1 = \left ( \hskip -1ex\begin{array}{c} 1 \\ 0 \end{array}\hskip -1ex \right ) a + \left ( \hskip -1ex\begin{array}{c} 1 \\ 1 \end{array}\hskip -1ex \right ) b.}
Supongamos que el resultado es cierto para un número natural n \in \mathbb{N}. 

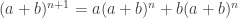 Observemos que (a+b)^{n+1} = a(a+b)^n + b(a+b)^n. 
Aplicando ahora la hipótesis de inducción resulta
\displaystyle{(a+b)^{n+1} = \sum_{k=0}^n \left ( \hskip -1ex\begin{array}{c} n \\ k \end{array}\hskip -1ex \right ) a^{n+1-k}\,b^k + \sum_{k=0}^n \left ( \hskip -1ex\begin{array}{c} n \\ k \end{array}\hskip -1ex \right ) a^{n-k}\,b^{k+1}.}
El segundo término de la derecha se puede expresar como
\displaystyle{\sum_{k=1}^{n+1} \left ( \hskip -1ex\begin{array}{c} n \\ k-1 \end{array}\hskip -1ex \right ) a^{n+1-k}\,b^k,}
de donde se sigue que
\displaystyle{(a+b)^{n+1} = a^{n+1}+b^{n+1} + \sum_{k=1}^n \left [ \left ( \hskip -1ex\begin{array}{c} n \\ k \end{array}\hskip -1ex \right ) + \left ( \hskip -1ex\begin{array}{c} n \\ k-1 \end{array}\hskip -1ex \right ) \right ] a^{n+1-k}\,b^k.}
Teniendo en cuenta la identidad de Pascal
\displaystyle{\left ( \hskip -1ex\begin{array}{c} n \\ k \end{array}\hskip -1ex \right ) + \left ( \hskip -1ex\begin{array}{c} n \\ k-1 \end{array}\hskip -1ex \right )=\left ( \hskip -1ex\begin{array}{c} n+1 \\ k \end{array}\hskip -1ex \right ) }
se deduce que
\displaystyle{(a+b)^{n+1} = \sum_{k=0}^{n+1} \left ( \hskip -1ex\begin{array}{c} n+1 \\ k \end{array}\hskip -1ex \right ) a^{n+1-k}\,b^k,}
y esto completa el paso inductivo.
Publicado por en