
Tal vez, dado que el año pasado se concedió el nobel a Higgs por su trabajo teórico, corroborado por el descubrimiento del famoso bosón este año pueda parecer, según se comenta en la divulgación, que el tema está resuelto: el higgs es lo que da masa a las partículas.
Pero, la verdad es que el asunto es mucho mas sutil.
Voy a explicar primero porqué el mecanismo de Higgs no nos dice gran cosa, a nivel fundamental, sobre la naturaleza de la masa.
En teoría cuántica de campos la masa aparece cómo una constante en las ecuaciones o en los lagrangianos.
Por ejemplo, en el caso de una partícula escalar, regida por la ecuación de Klein-Gordon, es una constante que multiplica al término cuadrático
en el campo.
Algo similar ocurre en la ecuación de Dirac.
Aquí he escrito las ecuaciones manteniendo todas las unidades y evitando el uso de las unidades naturales (h=c=G=1) para que se entienda mejor porque hablamos de un término de masa.
En ambas ecuaciones tenemos un primer término “cinético”, que contiene las derivadas de la función de onda. El siguiente término contiene unas constantes que multiplica a la función.
Escribiendo las ecuaciones es difícil ver porque surgen esas constantes concretas y habría que atender a la derivación de las ecuaciones.
Es más fácil verlo desde el lagrangaino.
El Lagrangiano de K-G es:

dónde 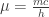
Y el de Dirac:

Aquí los términos de masa aparecen multiplicando a los términos cuadráticos en las correspondientes funciones de onda.
El motivo de que se interpreten como términos de masa proviene del análisis dimensional en cuyos detalles no voy a entrar, aunque no son muy complejos.
La idea es que el lagrangiano debe ser adimensional y que las funciones de onda de los campos tienen unas dimensiones naturales.
Los términos que multiplican a las funciones deben tener una dimensión tal que cada término sea adimensional.
Y, en el caso de los términos cuadráticos eso significa que lo que los multiplica debe tener dimensión de masa (o más bien energía, nótese el factor c^2).
Bien, eso significa que podemos poner un valor arbitrario a m, y tener partículas bosónicas escalares (ecuación de Klein-Gordón) y fermiónicas (ecuación de Dirac) con un valor arbitrario de su masa.
Y, desde luego, no necesitamos para nada el bosón de Higgs.
Esas ecuaciones describen partículas libres, pero si acoplamos las mismas a el campo electromagnético,
lo que vendría a ser la electrodinámica cuántica
(QED, por sus siglas en inglés) nos valdrían los mismos términos y seguiríamos teniendo que la masa no es nada más que una constante que aparece multiplicando a un término del lagrangiano y, una vez más, no es necesario el bosón de Higgs.
Cierto es que la QED no describe nuestro universo porque en ella no se incluyen las fuerzas nucleares fuertes y débiles (y mucho menos la gravedad), pero es una teoría cuántica de campos perfectamente válida.
El problema viene cuando uno quiere incluir bosones vectoriales masivos.
El electromagnetismo viene descrito por los campos eléctrico y magnético.
Estos pueden derivarse respectivamente de un potencial escalar y un potencial vectorial.
En relatividad general estos se combinan en un cuadripotencial que es el que aparecería en el lagrangiano.
Ese campo electromagnético describe fotones, bosones vectoriales, que son partículas sin masa.
Y esa es la clave, la ausencia de masa. Si queremos introducir bosones vectoriales con masa podemos hacerlo de manera similar a lo que se hace con la ecuaciónde Klein Gordon y la de Dirac y llegaríamos a la ecuación de Proca y su correspondiente Lagrangiano:

El problema de esta ecuación es que si se intenta introducir una interacción entre los campos vectoriales masivos que describe esa ecuación y un campo de Klein-gordon, o uno de Dirac, siguiendo el mismo procedimiento que se hace en QED se llega a que la teoría obtenida no es renormalizable, y por tanto inválida ya que no es predictiva.
Bien, ahí es cuando ya sí aparece el mecanismo de Higgs.
No he explicado, ni en esta entrada ni en ninguna anterior, cómo surgen en general los bosones vectoriales de una forma general, dentro de lo que se conoce cómo teorías de Yang mills.
Quien quiera leer detalles que consulte en la wiki sobre yang mills theory La idea general es que cuando uno tiene un lagrangiano que es invariante bajo una simetría global (la misma transformación de simetría en todos los puntos del espacio-tiempo) y la hace local (el mismo tipo de simetría, pero actuando localmente en cada punto del espacio-tiempo) uno debe introducir, para que el lagrangiano siga siendo invariante bajo la simetría local, unos campos que compensan ese cambio.
Esos campos van a ser los bosones vectoriales.
Cuando la simetría es el grupo de Lie U(1) se obtiene que el campo asociado es el electromagnetismo.
Cuando es SU(3) se obtiene que la teoría es la QCD (Quantum cromodynamics, la teoría cuántica de las interacciones nucleares fuertes). La interacción nuclear débil está asociada al grupo SU(2), combinado con el grupo U(1), pero ahí ya inerviene de manera fundamental el mecanismo de Higgs.
En las teorías de Yang-Mills todos los bosones vectoriales que aparecen son de masa nula.
Eso no es problema para el electromagnetismo como ya hemos dicho. pero las interacciones nucleares son de muy corto alcance y, por consiguiente, uno espera que las partículas mediadoras de esa interacción, los bosones vectoriales, tengan mucha masa, y, cómo hemos dicho, la teoría de Yang-Mills, que por lo demás es muy elegante, no nos sirve de nada. La teoría de Proca, con términos de masa directos para los bosones tampoco.
Bien, el mecanismo de Higgs, en cuyos detalles no entraré aquí (ver mecanismo de higgs en la wiki) lo que hace es que partiendo de una teoría de Yang-Mills con bosones sin masa acoplados a una teoría de Klein-Gordon que describe un bosón (el bosón de Higgs),
con masa y un término potencial elegido de manera apropiada, nos lleva a que cuando se produce un fenómeno conocido como ruptura espontánea de simetría.
La idea es que el grupo de simetría inicial se ve reducido cuando el bosón de Higgs toma un nuevo valor de vacío correspondiente a un valor de mínimo
(se supone que inicialmente estaba en un valor de máximo inestable).
Cuando uno reescribe el lagrangiano desarrollado alrededor del nuevo vacío del bosón de Higgs resulta que los campos vectoriales han obtenido un término de masa, relacionado con el potencial del bosón de Higgs, y que la teoría resultante si es renormalizable.
Digamos que, si quiere verse así, la masa de los bosones vectoriales se obtiene a partir de la energía potencial del bosón de Higgs.
Realmente los detalles son algo mas complejos, pero, más o menos, esa es una parte esencial de la idea.
Eso está bien, un término de masa está originado en un término de energía potencial.
Y, desde luego, nos da una teoría renormalizable que en la práctica nos permite obtener el modelo standard SU(3)xSU(2)xU(1), pero el caso es que el bosónde Higgs sigue teniendo su término de masa, de cuyo origen nada sabemos, y tampoco sabemos porque el potencial de Higgs tiene esa forma (no tenemos ninguna teoría fundamental que nos sugiera de dónde sale esa forma para el potencial, al menos hasta dónde yo sé).
Por cierto, he mencionado que el Higgs da masa a los bosones vectoriales.
Si uno hace los detalles de la teoría electrodébil se ve que también da términos de masa para los fermiones.
Sin embargo no toda la masa de los fermiones del modelo standard surge del mecanimso de Higgs.
Hay mas mecanismos implicados en cuyos detalles no voy a entrar.
En definitiva, el mecanismo de Higgs es algo útil, pero, en mi opinión no da una idea fundamental de qué es la masa.