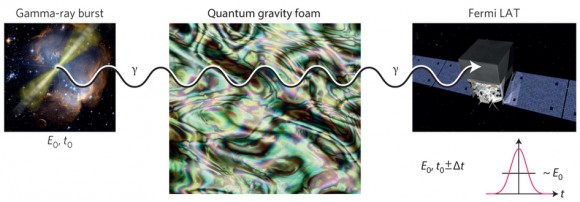
John Wheeler propuso que el espaciotiempo en la escala de Planck es una espuma cuántica. Una teoría cuántica de la gravedad que describa esta espuma cuántica debería violar la simetría de Lorentz de la teoría de la relatividad.
Para explorar esta espuma cuántica, Giovanni Amelino-Camelia y varios colegas propusieron en 1998 estudiar la relación energía-momento para un fotón que haya recorrido distancias muy grandes, es decir, estudiar si la velocidad de un fotón en el vacío depende de su energía (no es constante).
Gracias al telescopio espacial de rayos gamma Fermi LAT (Large Area Telescope) se han estudiado los fotones emitidos por el brote intenso de rayos gamma GRB 090510. No se observa que la espuma cuántica introduzca ninguna dependencia aleatoria de la velocidad de los fotones con la energía que siga una distribución normal al menos hasta una energía de 2,8 EPl al 95% CL (1,6 EPl al 99%).
Recuerda que EPl es la energía de Planck EPl ~ 1.22 × 1019 GeV.
Por tanto, no hay indicios de la existencia de espuma cuántica en la escala de Planck, recuerda LPl ~ 1.62 × 10−33 cm.
Nos lo cuenta Agnieszka Jacholkowska, “Quantum gravity: Spacetime fuzziness in focus,” Nature Physics, AOP 16 Mar 2015, doi: 10.1038/nphys3293; que se hace eco de Vlasios Vasileiou et al., “A Planck-scale limit on spacetime fuzziness and stochastic Lorentz invariance violation,” Nature Physics, AOP 16 Mar 2015, doi: 10.1038/nphys3270.
Cada escala de distancias tiene asociada una escala de energía; por ejemplo, LPl está asociada a EPl.
La espuma cuántica a cierta escala de distancias debería introducir una variación aleatoria de la velocidad de los fotones en el vacío v(E) = c + δv(E), donde δv(E) es una variable aleatoria que se distribuye de forma normal (gaussiana).
Por tanto, los momentos de llegada (T) de fotones emitidos por una fuente lejana deberían presentar una distribución T+δT(E), donde δT(E) es una variable aleatoria también distribuida de forma normal.
Gracias a ello se puede explorar una teoría cuántica de la gravedad que prediga una espuma cuántica hasta cierta escala de energía estudiando los fotones emitidos por brotes intensos de rayos gamma (GRB). Uno de los más intensos es GRB090510 que tiene desplazamiento al rojo z = 0,903 ± 0,001.
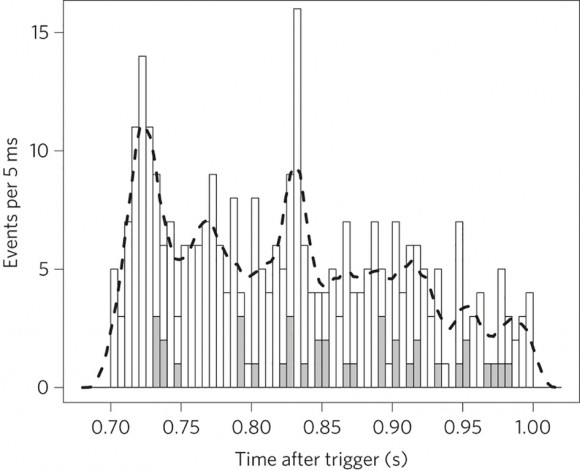
Su duración fue muy corta ~1 s, pero produjo fotones de muy alta energía (hasta ~31 GeV), con una curva de luz que muestra una estructura temporal fina con picos separados ~10 ms.
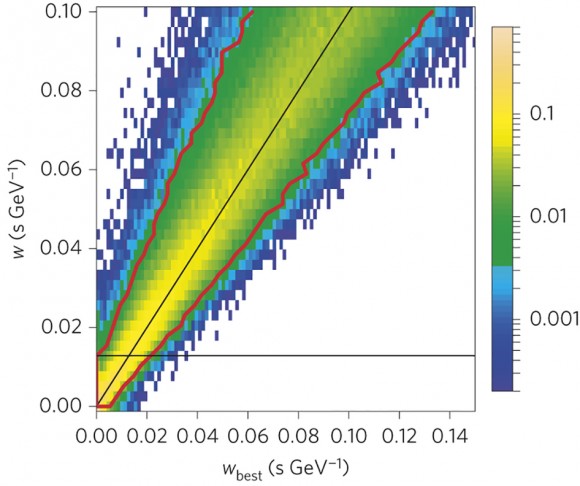
Se observaron 316 fotones con energía menor de Eth = 300 MeV y 37 fotones con energía más grande. Comparando la curva de luz con simulaciones por ordenador se puede estimar la cantidad w(z) = δT(E)/E. El intervalo de confianza se calcula usando el método de Feldman–Cousins
. Esta figura muestra el valor medido de la dispersión (wbest) para cada valor de la dispersión teórica (w). El resultado obtenido es wbest < 0,013 (0,023) s/GeV al 95% (99%).
A partir de este valor se obtiene el límite de energía 2,8 EPl para la escala de energía asociada a la espuma cuántica.
Por cierto, te recuerdo que en teoría de cuerdas es invariante Lorentz a todas las energías y todas las distancias. Gracias a la simetría del espejo (mirror symmetry) entre variedades de Calabi-Yau, las distancias R>LPl y 1/R< LPl son equivalentes (cuando R=1 es la escala de Planck).
La invarianza Lorentz se cumple a todas las escalas y no existe ninguna espuma cuántica que afecte a la velocidad de los fotones.
Por tanto, el nuevo límite restringe otras teorías cuánticas de la gravedad, como la gravedad cuántica de lazos (LQG) y las teorías que suponen que el espaciotiempo es discreto. En dichas teorías existe una espuma cuántica que viola la invarianza de Lorentz (al menos a la escala de Planck).
Para evitar el nuevo límite experimental hay que suponer que la dependencia de la velocidad de los fotones con la energía es superlineal (cuadrática o cúbica), estando suprimida la dependencia lineal (varias teorías, como LQG, se pueden ajustar para ello).
En resumen, un resultado experimental interesante que, aunque aporte poca información, apoya la teoría de cuerdas sobre sus competidores.