Vamos a ver si nos enteramos un poco de qué va eso del condensado de Bose-Einstein.
Si nos vamos a la wiki encontramos esta definición nada más empezar:
A Bose–Einstein condensate (BEC) is a state of matter of a dilute gas of weakly interactingbosons confined in an external potential and cooled to temperatures very near absolute zero(0 K or −273.15 °C[1]). Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at which point quantum effects become apparent on a macroscopic scale.
Traducción:
Un condensado de Bose-Einstein (BEC) es un estado de la materia de un gas diluido de bosones débilmente interactuantes confinados en un potencial externo y enfriados a temperatura muy cercanas al cero absoluto (0 K o -273.15 ºC). Bajo tales condiciones, una gran fracción de los bosones ocupan el menor estado cuántico del potencial externo, en este punto los efectos cuánticos se hacen manifiestos en una escala macroscópica.
Aquí voy a intentar explicar de qué va esto del condensado de una forma más visual.
Dualidad onda-partícula
Un ente/partícula cuántica se puede comportar como una partícula o como una onda según cómo decidamos medirla. Esto se conoce como dualidad onda-partícula.
Las partículas cuánticas se describen como si fueran ondas.
Y esta característica es la que nos proporciona todas las sorpresas del mundo cuántico.
De hecho, una partícula cuántica se puede describir como un paquete de ondas.
Una onda tiene una característica denominada longitud de ondas
En un gas tenemos una imagen en términos de partículas del siguiente modo:
Aquí el color representa lo siguiente:
Las partículas rojas son más veloces que las partículas azules. O dicho de otra forma, el momento de las partículas rojas es mayor que el momento de las partículas azules.
Esto es importante porque la temperatura de un gas no es más que un promedio de su energía (en este caso energía cinética). Es decir que es una función del momento promedio de las partículas que conforman el gas.
La longitud de onda de una partícula cuántica depende de su momento:
Esto es lo que dijo el señor de Broglie. Notemos que a menor momento mayor longitud de onda y viceversa.
Ahora si tenemos un gas lo cómodo es hablar en términos de temperaturas, que están relacionadas con el momento, así la longitud de onda de una partícula en un gas en términos de la temperatura es:
Como se llega de una fórmula a otra da un poco igual, lo importante es que a menor temperatura mayor longitud de onda, lo que corresponde con partículas con menor momento, es decir más lentas. Más azules.
Cuando hace frío
Ahora tenemos un gas de bosones.
Bosones sí, esas partículas de espín entero que ya hemos comentado.
Y nos pega por bajar la temperatura entonces empieza a ocurrir lo siguiente:
– Al bajar la temperatura (bajar el momento o la velocidad de las partículas del gas) la longitud de onda asociada de cada partícula se hace más grande.
– En un gas las partículas tienen una separación típica promedio. ¿Qué pasa cuando las partículas tienen asociada una longitud de onda comparable a la separación entre las partículas?
– En ese momento, es decir a una temperatura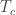 
, que llamaremos temperatura crítica, las ondas asociadas a las partículas se empiezan a superponer.
, que llamaremos temperatura crítica, las ondas asociadas a las partículas se empiezan a superponer.
– Si se empiezan a superponer significa que ya no podemos distinguir las partículas que tienen sus ondas asociadas unas de otras. Literalmente están en el mismo estado, con el mismo momento, y se comportan de forma coherente como un todo.
– Evidentemente el caso más extremo sería llegar al cero absoluto donde todas las partículas estarían en el mismo estado, el fundamental, el de menor energía permitida en el sistema, y con una única onda describiendo a lo que antes era un conjunto de partículas (onda superposición de todas las anteriores).
Esto está resumido en esta imagen:
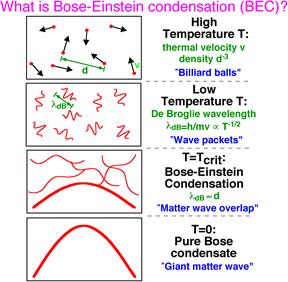
Eso es un condensado de Bose-Einstein.
Evidentemente eso no se puede conseguir con cosas fermiónicas (partículas de espín semientero), porque estas partículas no pueden estar en el mismo estado, por el Principio de Exclusión de Pauli.
Esto se realiza hoy a diario en laboratorios de todo el mundo y está abriendo puertas para muchas aplicaciones prácticas así como interesantes analogías teóricas con, por ejemplo, agujeros negros, radiación Hawking, explosión de supernovas, etc.
Les dejamos con una imagen famosa y un artículo de referencia:
Gas de átomos de rubidio. La imagen de la izquierda es justo en la temperatura de transición. Las siguientes son temperaturas más bajas. Esta imagen representa la distribución de momentos (velocidades). Lo que indica es que el sistema se concentra todo en un momento determinado, el menor posible para dicho sistema.
Este es un tema muy interesante que dará que hablar mucho en los próximos tiempos. Profundizaremos en él de vez en cuando.
Nos seguimos leyendo…
