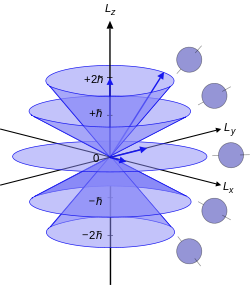
Llegados a cierto punto es imposible avanzar en conceptos que involucren física cuántica sin meter por el medio al elemento más chocante que se conoce en la misma: el espín. En esta entrada haremos algunas de las cuentas más elementales relacionadas con el giro de campos cuánticos para tener unas bases sobre las que seguir más adelante.
Energía potencial de giro:
El título de esta sección es un concepto solo cierto a medias. La energía potencial de giro, o centrífuga, encargada de alejar a los cuerpos en rotación de su eje de giro, no es una energía potencial usual. Surge como efecto de percepción cuando nos empeñamos en suponer que un objeto siga una trayectoria circular. Así, cuando estamos montados en un tiovivo podemos decir que hay una fuerza centrífuga que nos tira hacia fuera mientras que en realidad es el tiovivo el que nos tira hacia su eje giro y salir hacia fuera sería lo natural: seguir una línea recta.
No obstante, tratar la energía de rotación como una energía potencial resulta conveniente cuando las fuerzas que actúan en un sistema solo dependen de la distancia al observador, y se hace de una forma muy natural. Consideremos la
lagrangiana de una partícula libre en coordenadas polares sobre el plano:
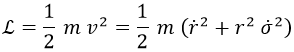
Recordemos que los puntos sobre variables denotan derivadas respecto al tiempo. Aquí tenemos sumadas la energía cinética y la de rotación.
En esta lagrangiana, una cantidad conservada es el momento angular L:
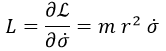
Y aprovechando esta expresión para redefinir la velocidad angular, es posible identificar como un potencial V que solo depende de r a la energía de rotación:
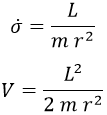
En esta entrada nos proponemos resolver la ecuación de Schrödinger sometida a este potencial.
La ecuación de Schrödinger en coordenadas esféricas:
Consideremos la ecuación de Schrödinger libre:
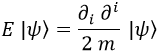
Las coordenadas cartesianas habituales x,y,z toman la siguiente forma en esféricas:
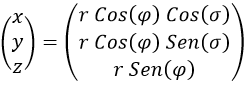
Aquí r representa la distancia al origen de coordenadas, σ el ángulo ecuatorial y φ el ángulo de elevación polar.
Cuando φ es nulo la coordenada z lo es también: estamos en el ecuador.
Análogamente, podemos descomponer la función de onda en un producto de tres funciones R, Θ y Φ dependientes de dichas variables dado que son ortogonales entre ellas y estamos en el caso libre:
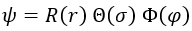
Para trabajar con la ecuación de Schrödinger necesitamos el laplaciano o derivada segunda vectorial en esféricas del campo. Esto requiere cálculo matemático delicado que ya comentamos aquí involucrando derivadas covariantes.
El gradiente del campo lo podemos reducir a una cuenta con derivadas parciales mediante la métrica g:
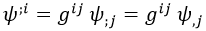
Teniendo el gradiente, podemos calcular su divergencia con la expresión obtenida en la entrada enlazada en el párrafo anterior:
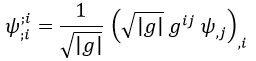
Y como la divergencia del gradiente es equivalente al laplaciano, ya tenemos la expresión para lo que queríamos.
La métrica covariante en esféricas, la contravariante y su determinante eran:
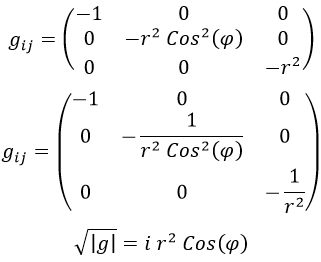
Los signos menos son debidos al convenio de la relatividad especial, como siempre.
Así pues, la cuenta que tenemos que hacer es:
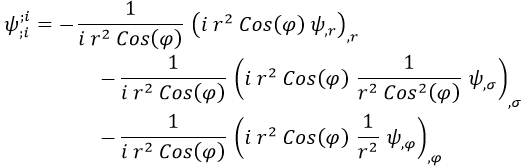
Cuya simplificación da:
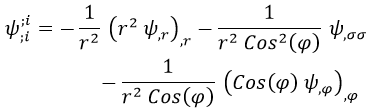
Sustituyendo en la ecuación de Schrödinger:
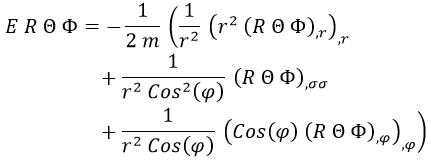
Y dividiendo todo por R Θ Φ:
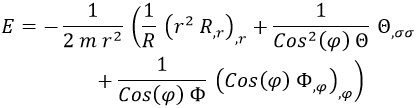
Aquí podemos identificar fácilmente la energía cinética y la energía rotacional:
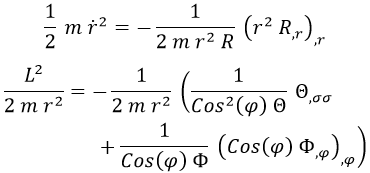
Solución angular:
Sabiendo que el momento angular se conserva por ausencia de fuerzas externas, podemos obviar la primera ecuación diferencial obtenida y, usando la segunda, describir el operador momento angular al cuadrado como:
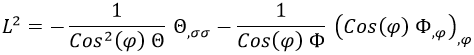
Al ser el momento angular una cantidad conservada, tendrá su propio autovalor, al que denominaremos como l (l+1) porque podemos llamarlo como queramos:
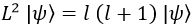
Sustituyendo en la ecuación de arriba:
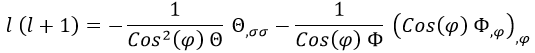
Y reagrupando:
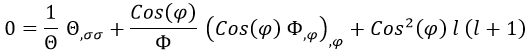
Tenemos un término que depende solo de σ y dos términos que dependen solo de φ. Podemos dar por hecho que si todo junto da cero es porque son opuestos y llamar m^2 a lo que suman los términos con φ de modo que:
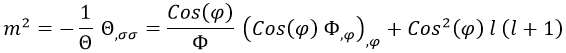
De la primera igualdad podemos despejar la función dependiente de σ aplicando que solo las exponenciales complejas tienen una derivada segunda opuesta a ellas mismas:
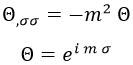
La segunda igualdad nos daría una ecuación diferencial tipo Legendre que nos permitiría despejar la función Φ, pero esto solo lo dejaremos indicado pues no será relevante la solución exacta para los objetivos de esta entrada:
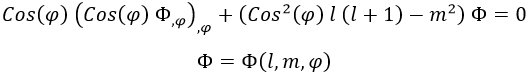
En suma, tenemos que cuando el momento angular se conserva, aparecen dos números cuánticos nuevos llamados número cuántico de giro l y número cuántico orbital m. Esto es aplicable al caso de los orbitales atómicos, donde los electrones están sometidos a una fuerza central que conserva el giro.
Veamos un poco más sobre el número m. El momento angular se define como un producto vectorial entre la posición y el momento lineal, y a su vez un producto vectorial se puede expresar en notación de índices con el símbolo alternante de Levi-Civita, de modo que la componente i-ésima de dicho vector es:
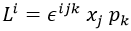
En concreto, la componente Lz del momento angular sería así:
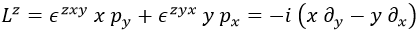
Aquí el signo – aparece porque el símbolo alternante se ve afectado por la métrica. Para reescribir la ecuación en esféricas necesitamos conocer la relación entre los parámetros esféricos y los cartesianos a la inversa:
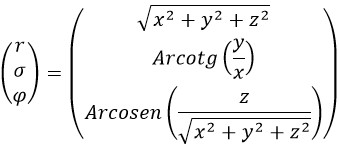
Para cambiar la derivada respecto a x por derivadas esféricas habría que hacer lo siguiente:
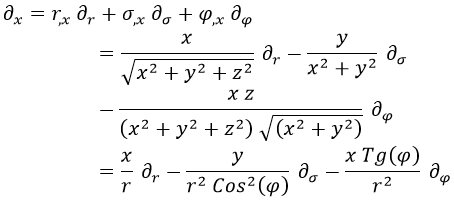
Las otras sustituciones a hacer serían:
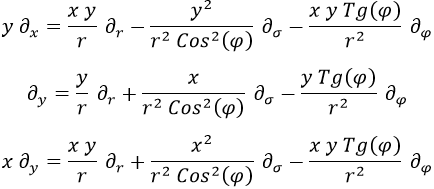
¿Y por qué dejo algunas cosas con x e y? Porque ocupan menos. Finalmente, Lz queda:
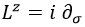
Teniendo en cuenta la forma del campo ψ, es posible analizar el efecto de aplizarle Lz:
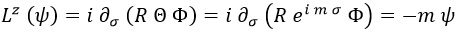
Y a partir de aquí resulta que m es el autovalor de mz:
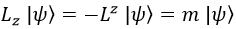
Nótese que la elección de cuál es el eje z queda a gusto de usuario en cada problema.
Ahora, si tenemos en cuenta que L2 se define en métrica espacio-tiempo con el siguiente producto escalar:
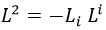
Como L2 es la suma de los cuadrados de Lx, Ly y Lz, necesariamente se cumple la siguiente desigualdad de valores medios:
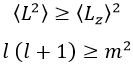
Esto limita en gran medida los valores que puede tomar m teniendo l.
Prefacio de bosones y fermiones:
Lo normal cuando tratamos con un campo en coordenadas esféricas es que tras dar una vuelta completa en σ nos encontremos en el mismo estado, ya que es el ángulo ecuatorial. Los campos con esta propiedad que parece obvia se llaman campos bosónicos, y para ellos se cumple que m necesariamente tiene que ser un número entero, pues de otro modo no se cumpliría la condición de periodicidad:
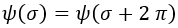
En el caso de que dar una vuelta completa al campo no fuese equivalente a no moverse, sino a invertirlo de signo, tendríamos un campo fermiónico que cumpliría:
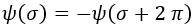
¿Y cómo es posible que girando un campo completamente no de lo mismo sino lo opuesto? Hay varias formas de representar esto geométricamente, pero no para justificarlo de forma sencilla, así que simplemente diremos que pasa porque sabemos que pasa. Explicaciones más detalladas de por qué los fermiones tienen esta propiedad podrían requerir nueva física.
Pero centrándonos en lo que nos ocupa esta entrada, para que se de el caso es necesario que m sea un número semientero, es decir, de la forma impar/2.
Ya sea el campo bosónico o fermiónico, en todo caso los posibles valores de m variarían de uno en uno, y de ahí se puede concluir fácilmente que el valor máximo de m, sometido a la desigualdad vista con respecto a l, es l:
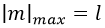
Cualquier valor más grande o no cumpliría la desigualdad o no cumpliría la relación de periodicidad adecuada. Se deduce de aquí inmediatamente para bosones que dado que para cada valor de l, tendremos todos los valores de mpositivos hasta él y los negativos, más el cero, un valor de l dado permite 2 l + 1 valores de m diferentes. En el caso de fermiones, se llega a la misma conclusión.
Incompatibilidad entre observables:
Hemos caracterizado L2 y Lz, pero a estas consideraciones les siguen otras preguntas relevantes: ¿Podemos medir ambos a la vez? ¿Y junto con las componentes Lx y Ly? Veamos qué nos dice Heisenberg.
El producto de incertidumbres entre dos operadores es el semimódulo del conmutador entre ambos:
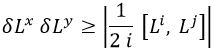
Así que para que dos componentes de L se puedan medir simultáneamente es necesario que su conmutador sea nulo. Tenemos que desarrollar el conmutador:
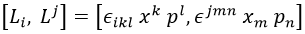
En primer lugar, los símbolos alternantes se pueden sacar fuera:
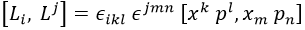
En segundo lugar tenemos en cuenta el conmutador canónico entre x y p, así como las operaciones que podemos hacer con conmutadores:
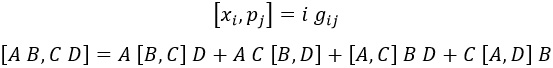
Sabiendo esto, podemos obviar los conmutadores de x con x y de p con p, y quedarnos con:
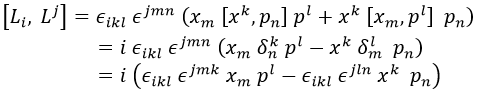
Ahora, aprovechando que tenemos símbolos alternantes con índices compartidos, recordamos la regla de contracción de los mismos adaptada a métrica espacio-tiempo:
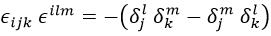
Con esta regla se llega finalmente a:
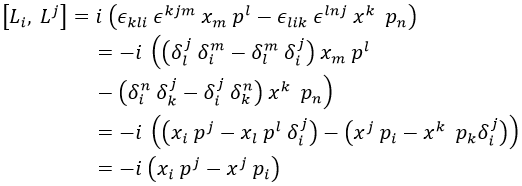
Y esto, aunque no sea evidente, es equivalente a esta otra forma de expresarlo:
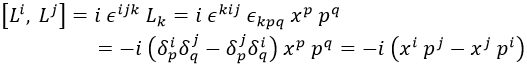
La equivalencia queda demostrada por demostración inversa.
Así pues, finalmente, las componentes de momento angular no conmutan y el producto de sus incertidumbres debe cumplir:
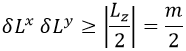
Consecuentemente, conocida una componente del momento angular, resulta imposible conocer las otras dos siempre que la conocida tenga m no nulo. Obviamente, si todas son nulas podemos conocer que el momento angular es cero.
En el caso en el que m es máximo, es decir, vale l, si la desigualdad se convierte en igualdad podemos suponer a priori por simetría:
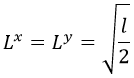
Y vemos que sumando valores esperados todo encaja:
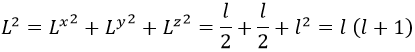
Cabe destacar, a parte, que L2 sí que conmuta con todas las componentes de L, con lo que siempre podemos medir simultáneamente los números cuánticos l y m:
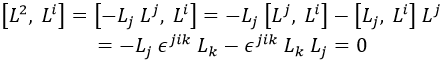
En la última línea el motivo por el que se anula todo es que estamos contrayendo índices simétricos con índices antisimétricos, de modo que tendremos algo menos ese mismo algo todo el rato.
Adición de momentos angulares:
Todos los conceptos vistos en esta entrada están hechos de forma genérica para un campo no sometido a ninguna fuerza que impida conservar el momento angular. Consecuentemente, sus implicaciones son válidas para cualquier observador que sea respetuoso con esa condición.
Así pues, si yo observo un campo con momento angular l1, y otro me observa a mí con momento angular l2, ese otro verá al campo con la suma (o resta) de nuestros momentos angulares. En particular, si tenemos un fermión con momento angular intrínseco o espín s, y lo observamos moviéndose en torno a un átomo con momento angular l, su momento angular neto j será la suma de ambos.
Respecto a las cualidades fundamentales de composición de momentos:
- La composición de dos campos bosónicos da lugar a un nuevo campo bosónico (Dos fotones juntos se pueden considerar como un único fotón con las propiedades sumadas de ambos).
- La composición de dos campos fermiónicos juntos también da lugar a un campo bosónico (Dos electrones juntos con espín opuesto serían como un bosón. Es más, un electrón y un antielectrón juntos pueden dar lugar a un fotón).
- La composición de un campo fermiónico con uno bosónico da lugar a uno fermiónico (En el ejemplo de los orbitales,j es fermiónico).
Todo esto se demuestra trivialmente considerando las posibles sumas de sus números cuánticos l.