Perdámosle el respeto a la matemática y encontraremos cosas increíbles.
El juego
El objetivo del juego es:
- Introducir algunos símbolos a nuestra elección.
- Definir un par de operaciones a nuestra elección también.
- Jugar un poco con ellos y sacar dos o tres expresiones.
¿Jugamos? El objetivo de esto es simplemente eso, jugar. Y por lo demás nos llevaremos una agradable sorpresa que será desvelada si todos hemos seguido el juego. Por supuesto nosotros vamos a desarrollar todas las expresiones explicándolas paso a paso, detalladamente. Si alguno de vosotros ha seguido el juego… desvelaremos por qué hemos jugado.
ELEMENTOS INICIALES:
En esta sección vamos a definir algunos símbolos y una operación. Más adelante cuando el juego se vaya “complicando” iremos introduciendo otros:
= A este símbolo lo llamaremos “a”
= A este símbolo lo llamaremos “a daga”
- Tanto
como
serán nuestros objetos básicos.
Una vez definidos los símbolos ahora definamos una operación que llamaremos “paréntesis”:
- Definimos la operación
- Esta operación es simplemente una regla de manipulación, y en este caso elegimos que dados dos símbolos cuales quiera
y
genéricos, es decir, que son combinaciones de
y
arbitrarias ya que, por ahora, estos últimos son los únicos símbolos que hemos definido. La regla de manipulación es:
Así podremos poner: ![\left[a,a^\dagger\right]=aa^\dagger - a^\dagger a \left[a,a^\dagger\right]=aa^\dagger - a^\dagger a](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%2Ca%5E%5Cdagger%5Cright%5D%3Daa%5E%5Cdagger+-+a%5E%5Cdagger+a&bg=ffffff&fg=333333&s=0) y claro, esto así dice poco, hemos de fijar un valor de referencia (igual que decimos 1+1=2 y a partir de ahí vamos subiendo). El valor que elegimos de referencia es:
y claro, esto así dice poco, hemos de fijar un valor de referencia (igual que decimos 1+1=2 y a partir de ahí vamos subiendo). El valor que elegimos de referencia es:
Esto quiere decir que cuando veamos la operación: ![[a,a^\dagger] [a,a^\dagger]](http://s0.wp.com/latex.php?latex=%5Ba%2Ca%5E%5Cdagger%5D&bg=ffffff&fg=333333&s=0) para nosotros será como un señor 1.
para nosotros será como un señor 1.
Pero además quiere decir otra cosa, si tenemos una expresión donde aparece 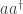 no podemos sustituirla por
no podemos sustituirla por  .
.
Es evidente de la definición de la operación paréntesis que se cumple lo siguiente:
El juego no da para más. Así que habrá que empezar a ampliar las reglas y los símbolos que pueden entrar.
NUEVOS SÍMBOLOS
Lo primero que uno puede hacer es probar con combinaciones de los símbolos básicos: 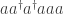 que podríamos escribir
que podríamos escribir 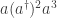 . Pero más vale ser un poco más modestos, aún no tenemos perfecto control del juego, lo cual es lógico porque nos lo estamos inventando.
. Pero más vale ser un poco más modestos, aún no tenemos perfecto control del juego, lo cual es lógico porque nos lo estamos inventando.
Así que juguemos con una combinación simple:  , bueno, para darle un poco de gracia al asunto empleemos
, bueno, para darle un poco de gracia al asunto empleemos  . Y como esta combinación vamos a usarla mucho, para no escribir tanto la llamaremos
. Y como esta combinación vamos a usarla mucho, para no escribir tanto la llamaremos 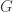 :
:
Y no podemos hacer mucho más que aplicar la operación paréntesis a ver que sale:
Calculemos ![\left[G,a\right] \left[G,a\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5BG%2Ca%5Cright%5D&bg=ffffff&fg=333333&s=0) y a ver que sale:
y a ver que sale:
Puuff!!, primer problema, nadie nos ha dicho como trabajar cuando tenemos sumas y esas cosas dentro de la operación paréntesis. Bueno, pues como el juego es nuestro nos inventamos dos reglas para esos casos:
Solucionado. Así que ahora podemos aplicar:
Otro problema, nadie nos ha dicho que pasa si tenemos números dentro de la operación paréntesis. Como no hay muchas ganas de pensar, toda combinación de [número, letra] o [letra,número] (siempre que el número esté solo) será cero. Con eso tenemos:
Más fácil no se puede.
Con lo que nos va quedando:
Y hete aquí, tenemos una combinación de símbolos  , pero nosotros sólo sabemos como se comporta la operación paréntesis
, pero nosotros sólo sabemos como se comporta la operación paréntesis ![\left[,\right] \left[,\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B%2C%5Cright%5D&bg=ffffff&fg=333333&s=0) cuando tenemos una
cuando tenemos una  y una
y una  . Así que intentemos ver que pasa cuando tenemos situaciones del tipo
. Así que intentemos ver que pasa cuando tenemos situaciones del tipo ![\left[AB,C\right] \left[AB,C\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5BAB%2CC%5Cright%5D&bg=ffffff&fg=333333&s=0) :
:
Vamos a decir que:
Por un lado el lado izquierdo da:
Y el lado derecho:
Por lo tanto hemos acertado con la regla que acabamos de introducir.
Así que aplicando esto a ![\left[a^\dagger a,a\right] \left[a^\dagger a,a\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%5E%5Cdagger+a%2Ca%5Cright%5D&bg=ffffff&fg=333333&s=0) obtenemos:
obtenemos:
Pero recordemos, ![\left[a,a\right]=0 \left[a,a\right]=0](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%2Ca%5Cright%5D%3D0&bg=ffffff&fg=333333&s=0) así que en este caso:
así que en este caso:
Pero claro, por la definición: ![\left[a,a^\dagger\right]=1 \left[a,a^\dagger\right]=1](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%2Ca%5E%5Cdagger%5Cright%5D%3D1&bg=ffffff&fg=333333&s=0) pero ¿cuánto vale
pero ¿cuánto vale ![\left[a^\dagger ,a\right] \left[a^\dagger ,a\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%5E%5Cdagger+%2Ca%5Cright%5D&bg=ffffff&fg=333333&s=0) ?
?
Por lo tanto: ![\left[a^\dagger a,a\right]= \left[a^\dagger ,a\right]a=-a \left[a^\dagger a,a\right]= \left[a^\dagger ,a\right]a=-a](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%5E%5Cdagger+a%2Ca%5Cright%5D%3D+%5Cleft%5Ba%5E%5Cdagger+%2Ca%5Cright%5Da%3D-a&bg=ffffff&fg=333333&s=0)
Así hemos llegado a: ![\left[G,a\right]=-a \left[G,a\right]=-a](http://s0.wp.com/latex.php?latex=%5Cleft%5BG%2Ca%5Cright%5D%3D-a&bg=ffffff&fg=333333&s=0) .
.
Siguiendo la misma cadena de razonamientos no es difícil llegar a ![\left[G,a^\dagger\right]=a^\dagger \left[G,a^\dagger\right]=a^\dagger](http://s0.wp.com/latex.php?latex=%5Cleft%5BG%2Ca%5E%5Cdagger%5Cright%5D%3Da%5E%5Cdagger&bg=ffffff&fg=333333&s=0)
Y ya está, hemos terminado de jugar con 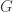 ,
,  y
y  .
.
Ahora vamos a proponer otra combinación que llamaremos 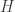 , y la obvia es:
, y la obvia es:
Donde  es un simple número, como 3, 5, etc.
es un simple número, como 3, 5, etc.
Vamos a ver si podemos simplificar esto, empleando la relación inicial ![\left[a,a^\dagger\right] \left[a,a^\dagger\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%2Ca%5E%5Cdagger%5Cright%5D&bg=ffffff&fg=333333&s=0) :
:
Vamos a elegir el primer término del paréntesis (,):
Por lo tanto:
Lo que nos queda:
Lo que es asombroso porque 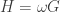 , así que no es fácil de llegar a:
, así que no es fácil de llegar a:
Para lo cual lo único que hay que tener en cuenta es que si tengo el producto de un número como 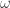 por uno de nuestros símbolos por ejemplo
por uno de nuestros símbolos por ejemplo  , el paréntesis
, el paréntesis ![\left[\omega A, B\right] \left[\omega A, B\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B%5Comega+A%2C+B%5Cright%5D&bg=ffffff&fg=333333&s=0) elegimos que nos de:
elegimos que nos de:
es decir, elegimos que si tenemos un número multiplicando a nuestros símbolos dentro de la operación paréntesis simplemente lo sacamos fuera y multiplica al paréntesis.
Así que no hemos avanzado mucho
Complicamos el juego un poco más
Vamos a meter más elementos en el juego, y vamos a meter cosas del tipo  . Y que sobre estos bichos actúen los símbolos que hemos definido previamente,
. Y que sobre estos bichos actúen los símbolos que hemos definido previamente,  ,
,  y
y 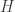 .
.
Reglas:
La regla que vamos a introducir es que cuando 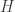 se pone en frente de
se pone en frente de  , lo vamos a llamar H actuando sobre
, lo vamos a llamar H actuando sobre  , nos da:
, nos da:
Y aquí viene una parte del juego interesante, tenemos que distinguir entre E y  . Para nosotros cuando tenemos solamente E representa un número y cuando tenemos
. Para nosotros cuando tenemos solamente E representa un número y cuando tenemos  es uno de los objetos de nuestro juego, es aquello sobre lo que pueden actuar
es uno de los objetos de nuestro juego, es aquello sobre lo que pueden actuar  ,
,  y
y 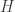 , es decir, no son lo mismo. No se confundirán números y estos bichos porque la notación es clara.
, es decir, no son lo mismo. No se confundirán números y estos bichos porque la notación es clara.
¿Cómo actúan  y
y  sobre los
sobre los  ?
?
Veamos este ejemplo:  .
.
El problema es que sólo sabemos como actúa 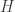 sobre
sobre  así que hagamos actuar
así que hagamos actuar 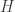 sobre
sobre 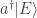 :
:
tenemos que buscarnos la vida para meter 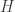 al lado de
al lado de  , para eso aprovechamos que
, para eso aprovechamos que ![\left[H,a^\dagger\right]=Ha^\dagger -a^\dagger H \left[H,a^\dagger\right]=Ha^\dagger -a^\dagger H](http://s0.wp.com/latex.php?latex=%5Cleft%5BH%2Ca%5E%5Cdagger%5Cright%5D%3DHa%5E%5Cdagger+-a%5E%5Cdagger+H&bg=ffffff&fg=333333&s=0)
Por lo tanto: ![\left[H,a^\dagger\right]+a^\dagger H \left[H,a^\dagger\right]+a^\dagger H](http://s0.wp.com/latex.php?latex=%5Cleft%5BH%2Ca%5E%5Cdagger%5Cright%5D%2Ba%5E%5Cdagger+H&bg=ffffff&fg=333333&s=0) , así tenemos:
, así tenemos:
Y esto queda:
Pero claro, aquí pasa algo, nosotros hemos impuesto que 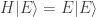 y ahora hemos encontrado que:
y ahora hemos encontrado que:
Lo que quiere decir que 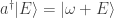
Siguiendo estos pasos, exactamente igual, se puede llegar a:
con lo que 
Es decir, al actuar con  sobre $|E\rangle$ lo convertimos en algo distinto, de forma que al actuar con H ya no obtienemos E sino
sobre $|E\rangle$ lo convertimos en algo distinto, de forma que al actuar con H ya no obtienemos E sino  . Análogamente con
. Análogamente con  pero disminuyendolo. Pero ahora vamos a imponer que hay un tipo de los bichos
pero disminuyendolo. Pero ahora vamos a imponer que hay un tipo de los bichos  que no puede ser disminuido más, y lo denotaremos por:
que no puede ser disminuido más, y lo denotaremos por: 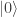 de forma que si aplicamos
de forma que si aplicamos  a este bicho directamente nos escupe cero:
a este bicho directamente nos escupe cero:
¿Y qué da 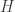 actuando sobre
actuando sobre 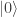 ? Pues hagamoslo recordando que
? Pues hagamoslo recordando que  tenemos:
tenemos:
Nos fijamos en que 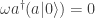 así que tenemos:
así que tenemos:
No está nada mal hemos encontrado un par de cosas interesantes con el juego este ¿no?
Rizando el rizo:
Bueno, pues vamos a tirar la casa por la ventana, ahora vamos a tener una familia de símbolos { } y los correspondientes {
} y los correspondientes { } donde tenemos infinitos de esos símbolos.
} donde tenemos infinitos de esos símbolos.
Como ciertamente es engorroso tener que escribir listas vamos a introducir una abreviatura para la lista, y llamaremos a la familia {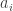 } donde
} donde  , esta
, esta  la llamamos etiqueta. Análogamente lo haremos para
la llamamos etiqueta. Análogamente lo haremos para  .
.
Ahora imponemos las siguientes relaciones:
Eso lo vamos a abreviar así: ![\left[a_i , a^\dagger_j\right]=\delta_{ij} \left[a_i , a^\dagger_j\right]=\delta_{ij}](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba_i+%2C+a%5E%5Cdagger_j%5Cright%5D%3D%5Cdelta_%7Bij%7D&bg=ffffff&fg=333333&s=0) , donde
, donde  es una abreviatura para:
es una abreviatura para:
Es cero cuando i es distinto de j y 1 cuando i es igual a j.
En todos los casos: ![\left[a_i , a_j\right]=0 \left[a_i , a_j\right]=0](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba_i+%2C+a_j%5Cright%5D%3D0&bg=ffffff&fg=333333&s=0) y
y ![\left[a^\dagger_i , a^\dagger_j\right]=0 \left[a^\dagger_i , a^\dagger_j\right]=0](http://s0.wp.com/latex.php?latex=%5Cleft%5Ba%5E%5Cdagger_i+%2C+a%5E%5Cdagger_j%5Cright%5D%3D0&bg=ffffff&fg=333333&s=0)
¿Ahora qué es 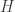 ?
?
Pues simplemente tomaremos:
es decir, sumamos todos los bichos uno por cada valor posible de la etiqueta i.
Hagamos actuar este H sobre 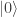 :
:
Bien podemos emplear esta expresión o si es más cómodo podemos emplear la expresión extendida:
Repitiendo lo que hicimos antes nos queda:
Pero estamos haciendo una suma de infinitos números del tipo 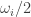 , siendo todos ellos positivos, el resultado nos da un infinito.
, siendo todos ellos positivos, el resultado nos da un infinito.
Y aquí tenemos que parar el juego, si algo te sale infinito ya deja de tener gracia.
Bueno, pues hasta aquí el juego este, esperamos que lo intentéis y tanto si os sale como si no, decidnos algo para desvelar el secreto que esto encierra.
Un placer como siempre.
http://cuentos-cuanticos.com/