En esta ocasión veremos, al fin, cómo podríamos hacer si quisiésemos introducir una cuerda en una teoría cuántica de forma acorde a las leyes de esta última.
Como primera conclusión tras jugar un poco con la idea, veremos que es inconsistente con la existencia de 3 dimensiones espaciales si respetamos los conceptos elementales de las matemáticas.
¿A quién y por qué le pareció una buena idea ponerse a cuantizar cuerdas?
En la década de los sesenta a los físicos teóricos les traía de cabeza comprender la estructura de los nucleones: el protón y el neutrón.
Las fuerzas nucleares eran bastante desconocidas a nivel estructural y los nucleones no interaccionaban con otras partículas como el electrón de forma puntual, así que era necesario suponer que tenían estructura interna.
Por otra parte, los resultados matemáticos de sus interacciones eran acordes con los que se podrían esperar si dentro de los nucleones hubiese cuerdas.
Este modelo fue planteado por el físico teórico Gabriele Veneziano. Posteriormente, otros teóricos como Miguel Virasoro, Yoichiro Nambu, Holger Nielsen y Leonard Susskind lo refinaron y plantearon que las oscilaciones de cuerdas cuánticas eran las generadoras de la estructura de la fuerza nuclear.
La aventura concluyó en 1974 cuando se popularizó la actual explicación de la misma: la cromodinámica cuántica.
No obstante, posteriormente se descubrió que la teoría de cuerdas tenía un alcance mayor del que se había imaginado inicialmente y por ello en las últimas décadas ha resurgido con fuerza, siendo el principal modelo de la física teórica.
Los conmutadores cuánticos. El punto de partida.
En mecánica cuántica, las principales conclusiones chocantes, como el principio de incertidumbre de Heisenberg, surgían de la existencia de conmutadores que, debiendo ser nulos, no lo eran.
El principal conmutador antiintuitivo se daba entre la cuadriposición X y el cuadrimomento P de una partícula, siendo este proporcional a la métrica g del espacio-tiempo:

En el caso de una hoja de cuerda, donde τ parametriza el tiempo y σ la posición sobre la cuerda, podemos trasladar el conmutador cuántico fundamental usando el cuadrimomento temporal y considerando que la métrica será la de Minkowski η:
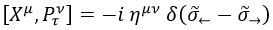
Aquí cabe destacar dos cosas. Hemos defido la posición σ← como aquella sobre la que actúa el operador de la izquierda del conmutador y σ→ como la posición sobre la cual actúa el de la derecha. Posteriormente, mediante una delta de Dirac hacemos que el conmutador solo surta efecto si son la misma.
Con esto conseguimos que al integrar el conmutador sobre todas las posibles posiciones de uno de los operadores se recupere exactamente el conmutador funtamental:
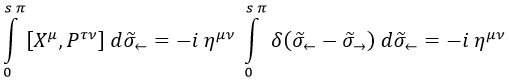
Recordemos que s valía 1 para cuerdas abiertas y 2 para cuerdas cerradas.
Dado que la delta de Dirac es simétrica es irrelevante sobre cuál de las dos posiciones integremos:
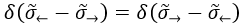
Conmutadores derivados:
Conociendo la relación entre el cuadrimomento temporal y la derivada temporal según la tensión T de la cuerda, podemos reescribir nuestro conmutador como:
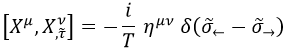
Por la simetría de Dirac, se cumple como se tiene que cumplir que:
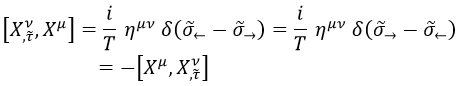
Antes de seguir, procede tener en mente cómo opera la regla cadena de las derivadas y tener claro que:
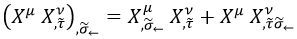
Gracias a esta relación, podemos asociar el conmutador entre la derivada natural de la cuerda y la temporal con la derivada natural del conmutador entre la cuadriposición y la derivada temporal:
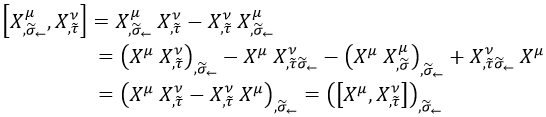
Con lo cual, dicho conmutador solo introduce como novedad una derivada de la delta de Dirac:
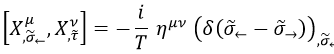
Procede indicar ahora que si una función es simétrica su derivada es antisimétrica y viceversa.
Con lo cual, para las derivadas de la delta de Dirac es cierto que:

A partir de aquí, podemos inferir que es cierto que:

Y, por último, cabe destacar las siguientes igualdades:
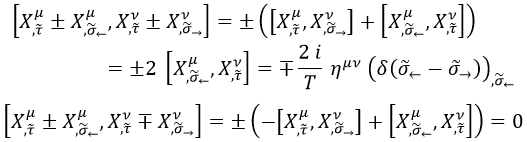
De entre estas, la particularmente relevante es la de arriba, y la usaremos inmediatamente.
Operadores de creación y destrucción de vibraciones:
Para la cuerda abierta, vimos que su movimiento cumplía la siguiente ecuación:
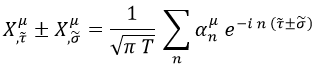
En el caso de la cuerda cerrada, la parte – de la ecuación indicada seguía siendo cierta, pero la parte + requería de otros cuadrivectores α:
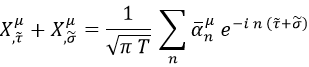
Consecuentemente, todo lo que demostremos para cualquier α que cumpla cualquiera de las ecuaciones de la cuerda abierta, será válido para los osciladores extra de la cuerda cerrada.
Quedémonos, para empezar, con las componentes trasversales I de oscilación, que ya justificamos en su momento que son las únicas interesantes:
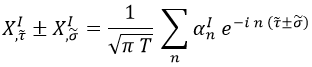
Consideremos ahora el conmutador de esta expresión consigo misma:
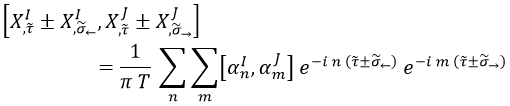
La parte de la izquierda la hemos calculado en la sección anterior de forma totalmente premeditada, así que podemos sustituirla:
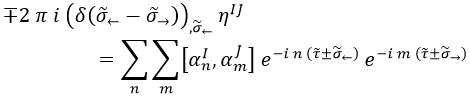
Y teniendo esto, nos interesa obtener el conmutador de α, que está metido en un doble sumatorio y por tanto no se puede despejar.
No obstante, una ecuación tiene que seguir siendo cierta siempre que en ambos miembros apliquemos cualquier operación que no destruya información, es decir, que sea invertible. Y cualquiera es cualquiera, así que iremos a lo loco con transformaciones de Fourier.
Antes de hacer el cafre, es conveniente indicar la siguiente igualdad a la cual querremos dedicar un templo:
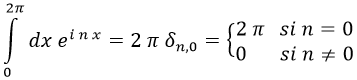
Su validez es obvia sin más que tener presente la fórmula de Euler de los números complejos y el hecho de que la integral de cualquier función tipo seno o coseno dentro de su periodo es nula.
La delta es una delta de Kronecker.
Podemos extender un poco este resultado integral y escribir lo siguiente:
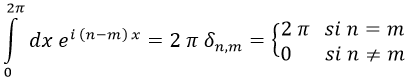
Una vez armados con esto, vamos a aplicar dos transformaciones de Fourier a cada miembro de nuestra ecuación de la cuerda para suprimir la dependencia con las diferentes σ.
Dicha transformación de Fourier simplemente consiste en integrar entre 0 y 2π lo que tengamos, multiplicado por una cierta exponencial compleja de fase proporcional a σ mediante un número entero y dividimos todo entre 2π.
Comencemos transformando mediante Fourier la parte derecha de la ecuación para cargarnos la dependencia con σ→:
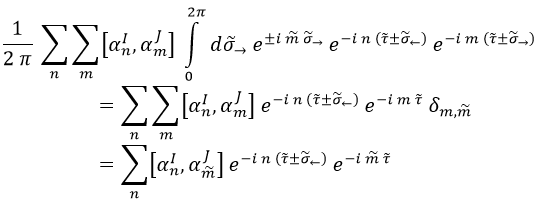
Fácil, ¿no? Con esto, gracias a la delta de Kronecker hemos conseguido cargarnos uno de los sumatorios. Sigamos con σ←:
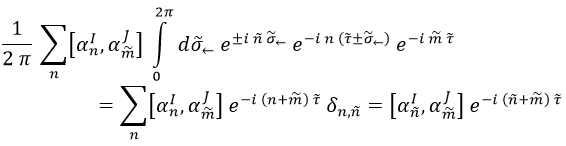
Y con esto ya nos hemos cargado los dos sumatorios.
Vayamos ahora con la otra parte de la ecuación.
Al aplicar la primera transformada de Fourier tenemos en cuenta que las derivadas e integrales respecto a variables diferentes conmutan para dejar la derivada de la integral de una delta en lugar de la integral de una derivada, lo que resulta en:
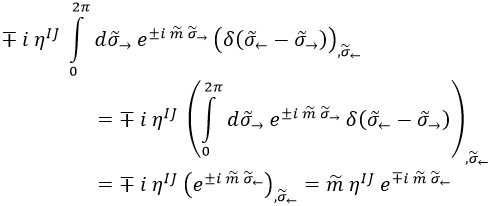
La segunda transformación vuelve a ser el mismo tipo de integral que las de antes:
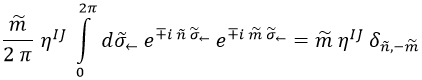
E igualando de nuevo los términos de la ecuación de la cuerda tras haber transformado mediante Fourier ambos dos veces:
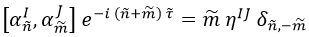
Ahora bien, si n+m es nulo la exponencial da igual y si no lo es también porque la delta de Kronecker se anularía.
Siendo este el caso, podemos recolocar todo obviando la exponencial y decir que:

Que en términos de la otra forma de definir los osciladores mediante la letra a implica:
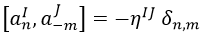
Lo cual, comparando con el conmutador cuántico usual que deben cumplir los operadores de creación y destrucción, lleva a la conclusión de que eso es lo que son a-n y an para la frecuencia de vibración n, siendo los primeros operadores de creación en el caso de n positivo y al revés en el caso opuesto:

Y una vez que tenemos los operadores de creación y destrucción de estados, ¡puede empezar la fiesta!
Estados cuánticos de las cuerdas y operador número:
Dada una cuerda abierta con un cuadrimomento p, podemos construir su estado ψ mediante la aplicación consecutiva (multiplicación) de operadores de creación de oscilaciones en todas las direcciones I trasversales y con todas las frecuencias n posibles. Cada uno lo aplicamos λnI veces:
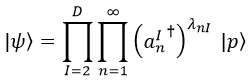
Para expresar los estados de las cuerdas cerradas tenemos que hacer lo mismo, pero con los dos conjuntos de osciladores que la caracterizan:
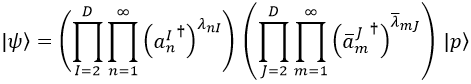
Teniendo esto, podemos definir el operador número N, que actuando sobre un estado tendrá que dar la suma de todas sus frecuencias de vibración activas multiplicada cada una por las veces que lo está:
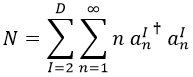
Es trivial ver que el operador número actuando sobre un estado sin vibraciones da 0, puesto que comienza actuando por la derecha con un operador de destrucción:

Por otra parte, lleva unas pocas líneas ver que el operador número actuando sobre el estado mJ da como resultado m por el estado.
Para ello solo necesitamos aplicar las propiedades de los conmutadores y los valores que sabemos que toman.
Por ejemplo, un operador de creación con otro siempre van a conmutar sin problemas, y lo mismo sucede con dos de destrucción:
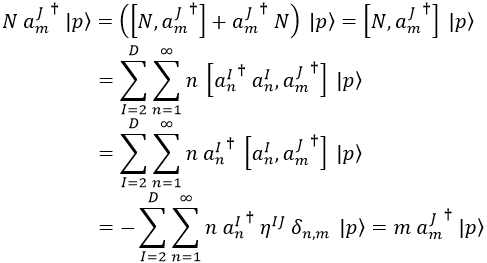
Como se puede ver, se le llama operador número porque da como resultado el número de la frecuencia del estado.
Supongamos que ahora queremos hacer que el operador número actúe sobre un estado general de una cuerda abierta:
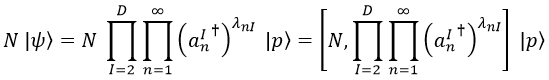
¿Qué podemos hacer con esta barbaridad?
Es bastante rebuscado de explicar, pero básicamente lo que podemos hacer es tener en cuenta que N conmutando con un producto de varias anI† elevadas a λnI es equivalente a la suma de los conmutadores de N con cada una de ellas multiplicada por su λnI respectivo y por todas las otras anI†. A partir de ahí, ya solo es cuestión de tirar para delante:
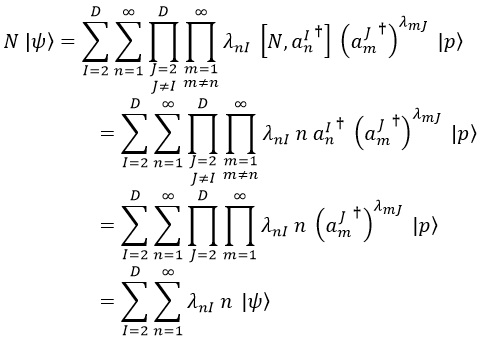
Así pues, llegamos a la conclusión esperada de que el operador número actuando sobre un estado de cuerda abierta da la suma de todas sus frecuencias activadas multiplicadas por el número de veces que aparecen.
¿Y qué pasaría con la cuerda cerrada?
Pues exactamente lo mismo, pero existiendo dos operadores número diferentes:
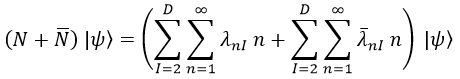
¡Ya tenemos cuantizadas nuestras cuerdas!
No obstante, las teorías requieren ser consistentes para poder ser tomadas en serio, y lo que hemos hecho implica una cosa extremadamente problemática…
Las dimensiones espaciales y el infinito. Una gran pega:
Retomemos los operadores de Virasoro, que en esta entrada estaban bastante marginados. Habíamos demostrado que el fundamental, L0, estaba relacionado con el cuadrimomento de la cuerda, por lo que cabe esperar que sea un operador medible y tome valores razonables. Su definición exacta era:

Podemos reescribirlo descomponiendo la suma de enteros en tres tramos: valores negativos, 0 y valores positivos:
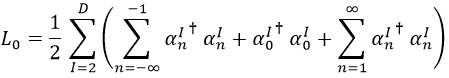
Aquí es importante recordar que:
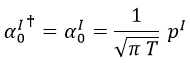
Con lo que atendiendo a definiciones podemos reescribir que:

Y usando las propiedades de los conmutadores, además, podemos reordenar el primer sumatorio de forma que:
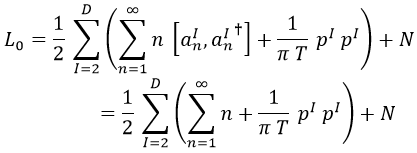
Y ahora viene el paso clave. En el primer término del paréntesis, en tanto que n no depende de I, podemos decir que lo sumamos D-1 veces y sacarlo fuera, con lo que queda:
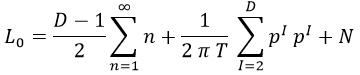
Hemos dicho que en tanto que L0 se relaciona directamente con el cuadrimomento debería tomar valores moderados.
Sin embargo, el primer término, al que podríamos llamar d, tiene una expresión que en principio es divergente y da infinito:

Esto, para cualquier persona “con dos dedos de frente” supondría un jaque mate al modelo y se pondría a hacer otra cosa.
La única posibilidad de evitar que de infinito sería que el número de dimensiones espaciales fuese una, la de la cuerda:
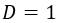
Ahora bien, si el universo tuviese una sola diversión la cuerda estaría sobre ella y no habría dimensiones trasversales sobre las cuales oscilar, con lo que es absurdo planteárselo siquiera.
Pero todavía quedaría otra posibilidad. ¿Y si la suma de todos los números naturales no diese infinito?
A los matemáticos se les empezarían a retorcer las tripas… pero podríamos fijar el número de dimensiones que quisiésemos.
En la próxima entrada sobre esto veremos (creo, si me entra en una) que de hecho hay otro motivo por el cual el número de dimensiones espaciales no podría ser 3 sino que tendría que ser de 25.