miércoles, 8 de julio de 2015

Momentos de la función distribución de partículas

Función distribución de partículas

Para los que no están familiarizados con la teoría de aerosoles, decir que una de las funciones más perseguidas es la función de distribución de partículas.

 Dicha función que denotaremos por 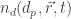n_{d}(d_p, \vec{r}, t) es una función que depende del diámetro de las partículas a considerar d_p, de la posición que ocupan dichas partículas \vec{r} y del tiempo t.

 Dicha función da una idea de cómo se distribuyen (de ahí su nombre, es obvio, ¿no? :P) las partículas en una determinada región del espacio, según su tamaño y para un momento determinado del tiempo.

Hay múltiples formas de “obtener” esta función de distribución de partículas.
 Una de ellas es resolviendo las ecuaciones de difusión para aglomerados de partículas.

 No es el objetivo de este post el ahondar en esta materia, la cual dejaremos para mejor ocasión.
Sí decir que una vez obtenida, podemos obtener mucha información de esta función de distribución. Para ello, se parte de la Teoría de Momentos.

Momento de una distribución de partículas

El momento de orden n de una distribución de partículas viene dado por la siguiente ecuación:
\displaystyle{M_{0}(\bar{r}, t)\, = \, \int_{0}^{\infty} n_{d}\cdot d_{p}^{\nu}\cdot d(d_{p})}
Esta función da el momento de orden \nu. Hasta aquí, todo esto puede parecer puramente matemático. Además no hemos hablado de distribuciones de partículas, ni de cómo obtenerlas. Tranquilos, todo se andará. 
De momento dejadme que os desglose un poquito más el significado físico de esta integral.


Significado de cada uno de los momentos

O mejor dicho: significado del orden de cada momento. 
Vamos a ir viéndolos para tener luego una especie de “recetario” donde ir viendo cada uno de los momentos y qué significan.
  • Momento de orden 0:

  •  Físicamente representa la concentración total de partículas para un instante dado y un punto dado: \displaystyle{M_{0}\, = \, \int_{0}^{\infty} n_{d}\cdot d(d_{p})\, =\, N_{\infty}}.

  • Momento de orden 1:

  •  Físicamente no tiene significado “per se”. Si se divide por el momento de orden 0, representa el diámetro medio de las partículas de la distribución: 

  • \displaystyle{\bar{d_{p}}\, =\, \frac{M_{1}}{M_{0}}\, =\, \frac{\int_{0}^{\infty} n_{d}\cdot d_{p}\cdot d\left(d_{p}\right)}{\int_{0}^{\infty} n_{d}\cdot d\left(d_{p}\right)}}

  • Momento de orden 2:

  •  Está relacionado con el área superficial de las partículas de la distribución por volumen de fluido en un sistema disperso. 
  • En otras palabras: superficie de partículas con relación al volumen del aerosol:

  •  \displaystyle{\pi\cdot M_{2}\, = \, \pi\cdot \int_{0}^{\infty} n_{d}\cdot d_{p}^{2}\cdot d(d_{p})\, =\, A}

  • Momento de orden 3:

  •  Manipulando un poco la expresión del momento de tercer orden se obtiene una relación de volúmenes: el volumen de las partículas con relación al volumen del gas en el cual se hayan inmersas: 

  • \displaystyle{\frac{\pi}{6}\cdot M_{3}\, = \, \frac{\pi}{6}\cdot \int_{0}^{\infty} n_{d}\cdot d_{p}^{3}\cdot d(d_{p})\, =\, \phi}. 

  • Puesto de otra forma: 

  • \displaystyle{\bar{v}\, =\, \frac{\phi}{N_{\infty}}\, =\, \frac{\pi\cdot M_{3}}{6\cdot M_{0}}}. 

  • Si están familiarizados con el concepto de porosidad, entendiéndolo como la fracción de volumen hueco dentro de un sólido; aquí vendría a representar como una antiporosidad, ya que el papel de los huecos (en realidad el aire o fluido dentro del espacio que no es sólido) lo representan las partículas; y el papel del sólido en este caso es un gas.

  •  El volumen promedio de las partículas se obtiene, como es lógico, dividendo por el momento de orden cero.

  • Momento de orden 4:

  •  Este momento está relacionado con el concepto desedimentación de partículas. Viene a representar la tasa a la que una superficie horizontal se cubre con partículas sedimentarias procedentes del aerosol: 

  • \displaystyle{\frac{\pi\cdot \rho_{p}\cdot g}{72\cdot \mu}\cdot M_{4}\, = \, \int_{0}^{\infty} (\frac{\pi\cdot d_{p}^{2}}{4})\cdot (\frac{\rho_{p}\cdot d_{p}^{2}\cdot g}{18\cdot \mu})\cdot n_{d}(d_{p})\cdot d(d_{p})}. 

  • Si se fijan bien, el término \displaystyle{c_{s}\, =\, \frac{\rho_{p}\cdot d_{p}^{2}\cdot g}{18\cdot \mu}} representa lo que se llama velocidad terminal de sedimentación de Stokes, con lo cual queda demostrada la relación de este momento con la tada de sedimentación, manejándolo apropiadamente.

  • Momento de orden 5: 

  • Como ven, la cosa se complica a medida que aumentamos el “orden” de los momentos. 

  • Este momento de orden 5 está relacioando con el flujo de material sedimentario desde un fluido. 

  • \displaystyle{\frac{\pi\cdot \rho_{p}^{2}\cdot g}{108\cdot \mu}\cdot M_{5}\, =\, \int_{0}^{\infty} n_{d}\cdot c_{s}\cdot \frac{\rho_{p}\cdot \pi\cdot d_{p}^{3}}{6}\cdot d(d_{p})}

  • Momento de orden 6:

  •  Este momento, que es el último interesante para nosotros, está relacionado con la dispersión producida por las partículas de aerosol.

  •  Si d_{p} << \lambda a lo cual se llama longitud de Rayleigh, entonces se tiene lo siguiente:

  •  \displaystyle{b_{sat}\, =\, \frac{2}{3}\cdot \frac{\pi^5}{\lambda^4}\cdot (\frac{m^2-1}{m^2+2})\cdot I\cdot \int_{0}^{\infty} m_{d}\cdot d_{p}^{6}\cdot d(d_{p}) \sim M_{6}}, siendo\lambda 

  • la longitud de onda de la radiación incidente, I la intensidad de la misma y m el índice de refracción de la partícula.
Desde el punto de vista que nos preocupará para los aerosoles, no hay momentos de mayor orden con un significado físico.
 Realmente, los momentos que más interesan son desde el momento de orden 0 al momento de orden 3, que tienen más relación con parámetros intrínsecos y de caracterización de dichos aerosoles.
 Los momentos de orden 4 y 5 están más relacionados con fenómenos de sedimentación. 
Y el momento de orden 6 con la respuesta a un haz de luz incidente en el aerosol.
Como siempre y para que podamos ver la utilidad de esto, supongamos que tenemos la siguiente ecuación n\left( x\, ,t\right)\, =\, \frac{N_{0}}{2\cdot \left( \pi\cdot D\cdot t\right)^\frac{1}{2}}\cdot exp\left[ \frac{-x^{2}}{4\cdot D\cdot t}\right] que satisface la ecuación monodimensional de difusión (esta ecuación será motivo de otro post).
Publicado por en