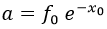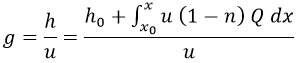Siguiendo con temas solicitados, en esta ocasión dedicaré una entrada a las bases de la resolución de ecuaciones diferenciales de primer orden de funciones de una variable.
En dichas ecuaciones se nos dan datos sobre la derivada de una función f que depende de x y se nos pide identificar qué función es exactamente.
Todas las ecuaciones fundamentales de la física son ecuaciones diferenciales, con lo que su utilidad práctica resulta evidente y no son pocas las veces que han sido resueltas en este blog, aunque sin haberles dedicado ninguna entrada en exclusiva.
Si bien la cantidad de tipos de ecuaciones diferenciales existentes es infinita, buena parte de las que pueden aparecer en problemas sencillos tienen estructuras bien clasificadas y es posible resolverlas teniendo en mente solo un puñado de trucos.
En esta entrada veremos cinco tipos de estas ecuaciones y la forma de resolverlas, centrándonos exclusivamente en las que involucran la primera derivada.
Además, veremos ejemplos de todas ellas y que no son excluyentes, de forma que lejos de haber una forma única de resolver cada caso uno puede sacarse de la manga varias formas diferentes.
Las funciones iguales a sus derivadas:
Esta pregunta la contestaremos varias veces a lo largo a modo de ejemplo polifacético: ¿qué funciones f cumplen ser iguales a sus derivadas f’?:
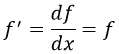
Como identificamos dichas funciones eran todas aquellas proporcionales mediante una constante a a la exponencial del número e, definido para ello:
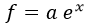
Ahora bien, uno podría no saberse esto de memoria.
Supongamos que sabemos que la derivada de cada una de estas funciones es igual a ellas mismas, pero no sabemos si puede haber otras que tengan esta propiedad. Veremos que no es el caso comprobando que ningún método de resolución de ecuaciones diferenciales da una respuesta diferente.
Ecuaciones diferenciales de variables separadas:
En este caso tenemos una ecuación diferencial en la cual se nos dice que f’ es igual a una función F dependiente de f multiplicada por otra función X dependiente de x:
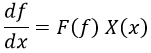
Para resolverlas, simplemente dejamos todo lo que depende de f quede a la izquierda y lo que depende de x quede a la derecha.
Después integramos:
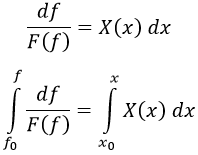
Una vez resueltas estas integrales, despejamos f y ya hemos acabado.
-Ejemplo trivial:
Si nuestra ecuación diferencial es la que iguala la derivada a la propia función, tenemos que:
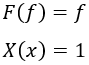
Con lo cual para resolver simplemente hacemos las siguientes cuentas:

Este resultado es el esperado sin más que hacer la siguiente identificación:
-Otros ejemplos:
Las ecuaciones diferenciales de variables separadas son, afortunadamente, muy corrientes en física.
Aparecen mismamente en la resolución de órbitas clásicas de planetas y en las ecuaciones de Friedmann para la expansión del universo.
Ecuaciones diferenciales de Bernoulli:
Este segundo tipo no es muy corriente verlo como tal y de hecho lo habitual es olvidarlo pasado cierto tiempo sin verlo. Una ecuación es de Bernoulli si tiene la siguiente apariencia:
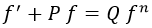
Aquí n es un entero y P y Q son funciones de x, al igual que f. En las ecuaciones diferenciales más corrientes n será siempre nulo, lo que simplifica extraordinariamente el proceso de resolución.
Cuando nos enfrentemos a una ecuación de este estilo lo primero que tenemos que hacer es considerar un cambio de variable y, en vez de con f, trabajar con g tal que:
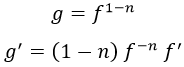
Nótese que si n es nulo g y f son la misma función.
Teniendo esto en mente, dividimos toda la ecuación de Bernoulli por f elevado a n y sustituimos:
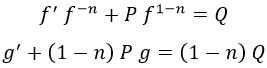
Ahora definimos la función u del siguiente modo:
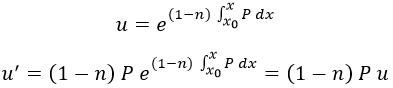
Y posteriormente definimos también h como:

Y usando h en la ecuación de Bernoulli podemos despejarla fácilmente del siguiente modo usando variables separadas:
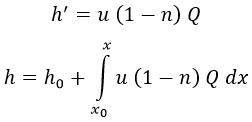
Teniendo h, se puede obtener fácilmente g:
Y por último, teniendo g se puede obtener fácilmente f:
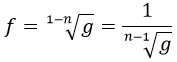
Y ya tenemos las reglas necesarias para resolver cualquier ecuación diferencial de Bernoulli.
-Ejemplo trivial:
Igualar la derivada de una función a ella misma puede escribirse como:
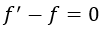
Y mediante simple aplicación consecutiva de todas las definiciones tenemos que:
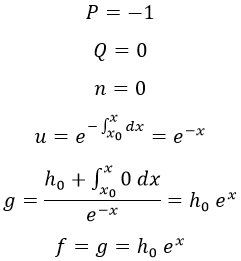
Y de nuevo obtenemos el resultado esperado, haciendo simplemente la identificación:
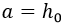
La ecuación de Bernoulli es demasiado general y en realidad incluye las variables separadas si Q es nulo, como sucedía en este caso, motivo por el cual uno puede pasarse toda una carrera técnica sin tener que saber este procedimiento de resolución. De hecho, en toda la trayectoria de este blog es la primera vez que resuelvo de este modo una ecuación de Bernoulli.
Ecuaciones diferenciales exactas:
En este caso se usan matemáticas algo más complejas y funciones de dos variables. Concretamente, vamos a trabajar con una función Φ que “dependa” de una variable λ y que esta, a su vez, dependa de f y de x.
La función será constante y tomará el valor C independientemente de λ.
De ahí las comillas que puse:
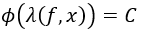
Siendo este el caso, podemos deducir que la derivada de Φ respecto a λ es nula. Y no solo eso: además podemos relacionar mediante la regla de la cadena multivariable dicha derivada con derivadas respecto a f y a x:
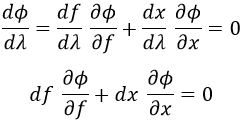
Pues bien, una ecuación diferencial es exacta si existe una función Φ que permite escribirla de la última forma.
Para saber si es el caso, tiene que cumplirse que las siguientes igualdades tengan sentido:
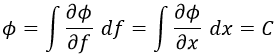
La mayoría de las veces no se podrán establecer estas igualdades porque la forma de Φ tras hacer la primera integral será incompatible con la forma de Φ tras hacer la segunda.
Para complicar aún más la cosa, una misma ecuación diferencial puede ser exacta o no según cómo coloquemos sus elementos.
-Ejemplo trivial:
Escribamos nuestra ecuación diferencial del siguiente modo:
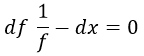
Aquí podemos identificar:
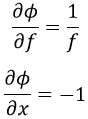
Al hacer la primera integral obtenemos que:
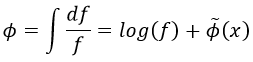
Aquí añadimos Φ∼ para considerar la dependencia con x que hayamos podido obviar.
Y al derivar este resultado parcialmente respecto a x:
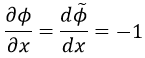
Y esto tiene sentido porque Φ∼ tenía como única condición no depender de f. Así pues:
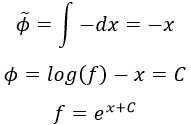
Y de nuevo hemos obtenido el resultado esperado sin más que identificar:
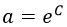
-Ejemplo trivial incompatible:
Supongamos ahora que hubiésemos dejado nuestra ecuación diferencial del siguiente modo:
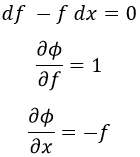
Al intentar resolverla por este método obtendríamos lo siguiente:
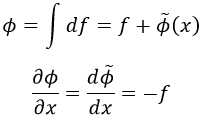
Y esto sería imposible dado que Φ∼ no puede depender de f. Como decíamos, una misma ecuación diferencial puede ser resoluble empleando este método o no según la forma en la que estén colocados sus elementos.
-Otros ejemplos:
Las ecuaciones diferenciales exactas pueden aparecer cuando uno trabaja con gradientes de campos escalares constantes, sobre todo durante los primeros cursos de teoría de campos.
El concepto de la función Φ en sí mismo sería un campo escalar.
Ecuaciones diferenciales lineales homogéneas de primer orden:
Estas son de las más importantes y tienen la siguiente forma:
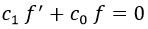
Aquí tanto c0 como c1 son constantes.
Esta ecuación se denomina lineal porque dadas dos soluciones diferentes la suma de ambas también es solución, homogénea porque a la derecha hay un 0 y de primer orden porque solo aparece la primera derivada.
Uno puede ver fácilmente que en realidad se trata de un tipo de ecuación de Bernoulli o de variables separadas si se recolocan los ingredientes de la forma adecuada.
No obstante, el método que veremos ahora tiene la ventaja frente a esos otros dos de poderse aplicar casi de la misma forma cuando la ecuación no sea homogénea y aparezcan más derivadas, cosa que con los otros no sucede.
Básicamente haremos algo que parece trampa pero que no lo es: estimar la forma de la solución.
Concretamente, estimaremos que la solución es de la forma:
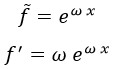
Teniendo esto, sustituimos en la ecuación y obtenemos que:
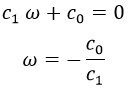
Y sabiendo esto, la solución general debe ser una cierta cantidad a de veces la exponencial planteada, por ser lineal:
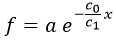
La ventaja de este método es que funciona con cualquier orden de derivadas siempre que la ecuación tenga la misma estructura.
Pero de eso tal vez hablemos en otra ocasión.
-Ejemplo trivial:
En esta ocasión más trivial que nunca, además.
Para nuestra ecuación:
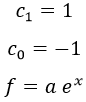
Ecuaciones diferenciales por serie de potencias:
Este método de resolución es, con mucha diferencia, el más general que existe, valiendo para cualquier tipo de ecuación diferencial existente siempre y cuando la función solución cumpla el “sencillo” requisito de ser derivable en todos los puntos infinitas veces.
Debido a su generalidad, no obstante, también es el más incómodo, no habiendo un solo caso en el que no de algo de pereza emplearlo.
En esencia se beneficia del hecho de que las funciones infinitamente diferenciables se pueden escribir como una serie de potencias de x. Por ejemplo, la serie de Taylor de potencias de la exponencial, como sabemos, es:
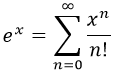
Así que simplemente lo que buscaremos hacer en esta ocasión es expresar la solución mediante su serie de potencias y obtener TODOS los coeficientes de la misma. ¿A que suena horrible? Lo es, además de sonar.
Como regla general, escribiremos f del siguiente modo:
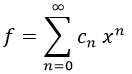
Y sus derivadas las obtendremos derivando cada uno de los miembros del sumando del siguiente modo:
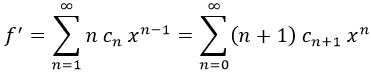
En el último paso cambiamos n por n+1.
Una vez hecho esto, sustituimos los sumatorios en la ecuación diferencial y calculamos todas las c una a una de forma que todo encaje para cada uno de los infinitos valores de n.
-Ejemplo trivial:
En nuestro caso, tras igualar la derivada a la función para cada valor de n obtendríamos:
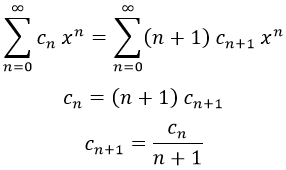
Esta última ecuación se denomina relación de recurrencia entre los términos, y sabiendo que cada término es igual al anterior dividido por su número, podemos generalizar y decir que:
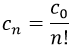
Y teniendo esto:
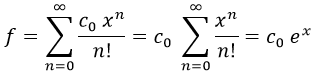
Con lo que por quinta vez obtenemos el resultado esperado. En esta ocasión teniendo que identificar simplemente:
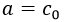
-Otros ejemplos:
El método de serie de potencias, desgraciadamente, es muy corriente en problemas complicados.
En mecánica cuántica se usa hasta respirar, por ejemplo resolviendo el oscilador armónico cuántico o el momento angular cuántico.
Es necesario también para obtener la precesión geodética de Mercurio.
En la próxima entrada sobre esto seguramente ahonde en ecuaciones diferenciales lineales.