
En esta entrada del minicurso vamos a comenzar un proceso por el que iremos aclarando algunos detalles. Nos proponemos explicar el formalismo que hay detrás de manera suscita y emplearlo para deducir muchas cosas de las que hemos ido insinuando por el camino.
La cosa se puede empezar a poner fea, ¿te vas a echar atrás ahora?

¿Qué es un estado?
Un estado en cuántica es todo lo que condensa la información que podemos obtener de un sistema físico. En términos formales es un objeto matemático, (un vector en un espacio de Hilbert, del que podemos obtener los valores de los distintos observables físicos. Ni más, ni menos.
Los estados cuánticos, representados por vectores (en un espacio de Hilbert, –omitiré tal pedantería en lo que sigue-) condensan toda la información que podemos extraer del sistema que esté describiendo tal estado.
Pero desgraciadamente dicha información no está explícitamente presente en el estado. Hay que hacerle cosas al estado para que de respuestas sobre los observables (cosas que podemos medir) físicos.
¿Qué es un observable?
Un observable es un objeto matemático denominado operador. Se denomina operador porque actúa sobre los estados y opera sobre ellos, los cambia de un modo conocido.
En realidad no todo operador representa un observable, para que así sea los operadores han de satisfacer dos condiciones esenciales. Han de ser lineales y han de ser hermíticos.
Pero esto se cumple en todos los ejemplos que vamos a emplear.
En el desarrollo que sigue señalaré dónde está el punto de que un operador que representa un observable sea lineal y hermítico. No tengáis prisa.
Determinar estados
Lo esencial para determinar los estados de un sistema es elegir qué observable queremos conocer del mismo. Podemos querer estudiar posiciones, momento, espines en distintos ejes, etc.
En nuestro ejemplo, nuestras partículas tiene una característica denominada color. Esta característica se puede medir, es un observable físico, así que estará representada por un operador que denotamos por  .
.
Resulta que experimentalmente obtenemos midamos la partícula que midamos (que no conocemos su estado inicial) o blanco o negro. No hay más opciones, siempre nos sale blanco o negro.

Si esos son los resultados experimentales tenemos que aceptar que tenemos dos estados básicos de color, el estado blanco y el estado negro.

¿Ven la lógica? Es la naturaleza, el experimento, el que en definitiva ha de determinar los estados. Nosotros solo los ponemos en un formato matemático.
El operador  actúa sobre esos estados. En el caso de estos estados blanco y negro sabemos que cuando intentamos determinar el color de los mismos nos sale en la máquina (+1=Blanco) o (-1=Negro).
actúa sobre esos estados. En el caso de estos estados blanco y negro sabemos que cuando intentamos determinar el color de los mismos nos sale en la máquina (+1=Blanco) o (-1=Negro).
Eso significa que matemáticamente hemos de tener:

De ahí hemos de poder inferir la forma del operador  . La cuestión es, ¿cómo construimos matemáticamente el operador?
. La cuestión es, ¿cómo construimos matemáticamente el operador?
Pues no hay mucho donde elegir en este punto, solo tenemos los estados cuánticos a nuestra disposición, el blanco y el negro.
Así que la forma del operador construida con ellos ha de ser:

Como hemos dicho antes para que el operador  represente un observable físico ha de ser lineal y hermítico. ¿Qué es eso de hermítico?
represente un observable físico ha de ser lineal y hermítico. ¿Qué es eso de hermítico?
PUEDES SALTAR ESTA SECCIÓN EN AZUL SI NO QUIERES ENTRAR EN DETALLES DE HERMÍTICOS
Dado un operador, por ejemplo nuestra  , podemos calcular otro operador que denominamos el hermítico asociado del original. El hermítico asociado a un operador
, podemos calcular otro operador que denominamos el hermítico asociado del original. El hermítico asociado a un operador  se denota por
se denota por 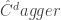 .
.
Un operador se dice que ES HERMÍTICO si él y su hermítico asociado son iguales. Es decir, si se cumple que  .
.
Para fijar ideas:

¿Cómo se calcula el hermítico asociado de un operador  ?
?
Vayamos por casos. Por un lado podemos tener:
Ale, ya sabemos calcular hermíticos asociados.
Bueno, tal vez haga falta un poco más en lo que nos ocupa:

No es ta difícil, ¿verdad? Pues nada, ya podéis demostra que  .
.
Nuestro operador ES HERMÍTICO. Por lo tanto tiene toda las papeletas para poder representar un observable físico. (Ojo, los observables vienen representados por operadores hermíticos, pero no todos los operadores hermíticos tienen que representar un observable físico).
Así que asumiendo que nuestro operador es hermítico, como tiene que ser,  , ¿Por qué es importante que sea así?
, ¿Por qué es importante que sea así?
Hay dos motivos gordos (son teoremas matemáticos):
1.- Los estados propios de los operadores hermíticos son vectores de módulo unidad (esto siempre se puede conseguir) y son perpendiculares entre sí. Y eso, os recuerdo, que se traduce en estas condiciones matemáticas que hemos venido usando:

2.- Un operador hermítico actuando sobre uno de sus estados propios siempre devuelve el mismo estado multiplicado por un números (este número se denomina valor propio).
Estos números, los valores reales, siempre son números reales.
Como así ocurre en nuestro en nuestro caso como no podía ser de otra forma:

Los valores propios de los operadores hermíticos son reales y eso es bueno, muy bueno, ¿por qué?. ¿Recordemos lo que nos dice la cuántica sobre los posibles resultados de las medidas sobre un estado físico de un determinado observable? La cuántica nos dice que lo únicos resultados posibles son los valores propios del operador que represente al observable.
Así que es bueno que salgan números reales, nosotros no sabemos medir otro tipo de números .
La física cuando se viste de matemática es maravillosa.
Lo dejamos aquí para reposar un poco el tema.
Nos seguimos leyendo…
