Hay cierta confusión acerca de si la mecánica cuántica y la relatividad especial son compatibles.
En esta entrada vamos a ver que sí lo son pero no en la forma en la que uno esperaba.
La ecuación de Schrödinger
Como hemos visto para estudiar como evoluciona en el tiempo un sistema cuántico no relativista (y aquí por no relativista nos referimos a que no sigue la relatividad especial, porque la relatividad Galileana sí que la sigue, recordemos que toda la física es relativista en uno u otro sentido) empleamos la ecuación de Schrödinger.
La ecuación de Schrödinger no es más que el Hamiltoniano traducido a las correspondientes variables cuánticas que representan las magnitudes que podemos medir, los observables.
Clásicamente el Hamiltoniano es la suma de la energía cinética más la energía potencial que tiene el sistema cuántico bajo estudio, para fijar ideas una partícula.
La energía cinética de una partícula de masa m es:
Y su energía potencial vendrá dada por una expresión que por ahora supondremos que sólo depende de la posición de la partícula
la forma de este potencial dependerá de la interacción que estemos considerando.
Por lo tanto el Hamiltoniano será:
que no es más que la energía total: 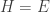
Ahora usamos la correspondencia entre las cantidades clásicas y los operadores cuánticos que representan los observables:
Las posiciones actúan multiplicando el estado cuántico (representado por la función de onda 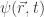 por su posición:
por su posición:
El momento clásico, no relativista:
Se traduce por:
Esto actúa derivando el estado cuántico representado por la función de onda 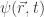 respecto a la coordenada indicada:
respecto a la coordenada indicada:
Si agrupamos, tenemos lo siguiente:
Por no escribir mucho nos inventamos una notación para simplificar esto:
Por lo tanto la energía cinética será:
Donde 
Por último la energía total clásica E cuánticamente es:  .
.
Poniendo esto todo junto en la ecuación de Schrödinger:
Y llegó la relatividad
Ahora en vez de tomar la ecuación de la energía total como suma de la energía cinética más la potencial, tomemos la relación relativista de la energía:
Haciendo las sustituciones anteriores:
Aquí estamos en relatividad, así que las coordenadas espaciales y temporales están en pie de igualdad.
Podríamos agrupar por tanto la cosa de esta forma:
La cantidad
la denotamos por 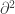 con lo que queda:
con lo que queda:
Esta es la conocida como la ecuación de Klein-Gordon.
De hecho esta es la ecuación más evidente para unir la cuántica con la relatividad especial.
Lo curioso es que históricamente Schrödinger llegó a esta ecuación antes que a la que lleva su nombre pero debido a ciertos problemitas de interpretación no se decidió a publicarla.
Problemas de interpretación.
El problema con la ecuación de Klein-Gordon es que dado un estado cuántico de una única partícula representado por una función de onda 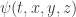 la energía de dicha partícula será:
la energía de dicha partícula será:
Es decir, la partícula tendría energía positiva o negativa.
Uno podría decir, bueno pues las energías negativas no las consideramos, es simplemente una solución matemática pero que no tiene sentido físico.
Sin embargo esta postura no es adecuada por diversos motivos:
Para que la teoría cuántica tenga sentido hemos de aceptar ambas soluciones. Si no consideramos las soluciones con energías negativas perdemos la posibilidad de resolver la ecuación de Klein-Gordon.
Sin embargo, la energía de las partículas que nos rodean siempre son positivas. Así que tenemos un problema gordo a la hora de aceptar dichas energías negativas.
Además una teoría con energías negativas es fundamentalmente inestable.
Una teoría ha de tener un mínimo de energía. ¿Por qué?
Porque los sistemas tienden a ir a su estado de menor energía, pero si permitimos energías negativas, no tenemos tal mínimo.
Un sistema podría empezar a ir de un estado de energía E a estados de energía cada vez menor.
Pero recordemos que cuando pasamos de un estado de energía E a un estado de energía E’, E>E’, la diferencia de energía se emite en forma de radiación E-E’.
Si la partícula cada vez pasa a un estado de menor energía veríamos una emisión continua y sin final de energía por todos lados, de hecho moriríamos abrasados (no moriríamos porque la vida no sería posible
El problema es la soledad.
Este problema en realidad no es tal, evidentemente, nuestro universo no es así. ¿Entonces esto quiere decir que la relatividad especial y la cuántica no son compatibles? En absoluto, el problema es simplemente interpretativo.
Estamos pensando en una partícula descrita por la ecuación de Klein-Gordon. Esta ecuación combina la relatividad especial y la teoría cuántica, y por tanto dicha partícula se está moviendo a velocidades cercanas a la de la luz en el vacío.
Pero claro, resulta que aquí entra en juego la famosa ecuación:
Esta ecuación representa una equivalencia (más que una igualdad).
Es decir, la masa de una partícula no es más que otra forma de energía y por tanto uno puede transformar energía en masa (transformación de energía) igual que podemos transformar energía cinética en calor o en energía potencial.
Sin simplemente transformaciones de energía en distintos formatos.
Entonces resulta que si la partícula alcanza el régimen de velocidades relativistas puede tener la suficiente energía como para crear (sí, crear literalmente) nuevas partículas siempre que se respeten las leyes de conservación (energía, momento, carga, etc).
Por lo tanto, la ecuación de Klein-Gordon no puede describir una única partícula.
De hecho, lo que describe tal ecuación es un campo (una característica que toma un valor en cada punto del espaciotiempo) y que puede tener excitaciones que se presentan como partículas (recordemos que en este contexto una partícula es algo con masa definida, carga definida y espín definido, no es una pelotita).
Y si uno toma este punto de vista, las “energías negativas” no son tales.
Los estados que parecen tener “energías negativas” en realidad representan antipartículas.
En virtud de lo anteriormente comentado, podemos crear partículas, pero pueden ser de materia o de antimateria y resulta que el signo ese que nos traía de cabeza simplemente nos dice si estamos hablando de una partícula de materia o de antimateria.
Y así, se resuelve el problema.
Así que, una de las cosas más asombrosas de la unión entre relatividad especial y teoría cuántica es que:
No podemos hablar de una única partícula sino que tenemos que pensar en términos de campos.
Lo cual nos lleva a la teoría cuántica de campos.
Para que la teoría sea consistente hemos de aceptar la existencia de antimateria.
Esperamos haber podido explicar el inicio, la necesidad y el origen de la teoría cuántica de campos, que es el marco donde conviven los principios de la relatividad especial y la cuántica.
Eso nos lleva a que existe la antimateria (que se puede considerar un producto relativista) y que en esos niveles no podemos hablar de una única partícula.
Nos seguimos leyendo…