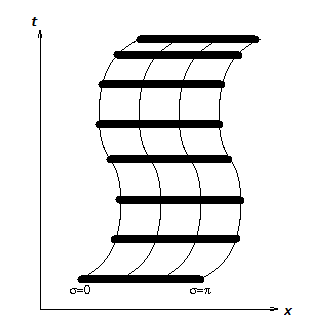
Una cuerda (línea negra) moviéndose en la coordenada temporal genera una superficie llamada hoja de cuerda.
Una de las teorías más famosas dentro del mundo de la física teórica es la teoría de cuerdas, sobre la cual ya hablé a nivel divulgativo por aquí. Dentro de dicho modelo, todas las partículas que observamos en nuestro universo son en realidad diminutas cuerdas vibrando que generan todos los efectos percibidos.
En esta entrada empezaré a adentrarme en esta idea técnicamente para ir viendo cómo surgen todas las ideas revolucionarias. Y, como no podía ser de otra forma, lo primero que tenemos que hacer es conocer cómo se trabaja con una cuerda normal y corriente en física.
Dinámica de la partícula clásica:
Cuando en física clásica queremos trabajar con una partícula en movimiento, definimos su lagrangiana L como la diferencia entre su energía cinética Ec y su energía potencial Ep. Esta lagrangiana puede depender de tres tipos de parámetros: las coordenadas xi de la posición en el espacio de la partícula, el tiempo t, y las variaciones temporales de sus coordenadas xi,t o velocidades. Las primeras y las terceras pueden depender de la segunda, pero nada más:
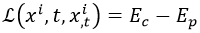
La derivada temporal la estamos representando con una coma previa a la t. Los índices i, por su parte, representan las tres coordenadas espaciales usuales, x, y y z, o semejantes según las que decidamos usar:
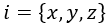
La lagrangiana, por su parte, tiene unidades de energía o de acción por segundo, dado que el parámetro del que dependen sus variables en conjunto es del tiempo.
Dada la lagrangiana de una partícula, podemos identificar el momento pi asociado a cada coordenada xi derivando la lagrangiana respecto a su velocidad xi,t:
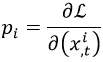
Por último, se tiene que cumplir que la derivada temporal del momento de la coordenada xi sea igual a la derivada de la lagrangiana respecto a dicha coordenada:

Y con esto tenemos caracterizado el movimiento de la partícula.
Si tuviésemos dos partículas en la lagrangiana habría que sumar las energías de ambas y obtener los momentos y ecuaciones de cada una por separado. Ahora bien, ¿qué pasaría si tuviésemos infinitas partículas pegadas, o si nuestra partícula no fuese puntual? Es necesario complicar un poco más la cuestión.
Dinámica de la cuerda clásica:
Lo que vamos a hacer aquí es, en esencia, lo mismo que hicimos cuando introdujimos la lagrangiana de Schrödinger yla del campo electromagnético, donde pasamos de tener como variable principal de la lagrangiana el tiempo a tener el tiempo y otras variables.
Al trabajar con una cuerda, su posición ocupa un segmento continuo de puntos, y por tanto no basta con fijar la energía cinética y potencial netas sino que hay que indicar sus energías ε por unidad de longitud:
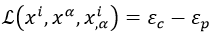
Nótese que esta lagrangiana tiene unidades de acción por segundo y metro debido a que va a depender de las dos variables etiquedadas por α de las que va a depender entonces el sistema, que son el tiempo t y la posición s sobre la cuerda:
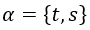
El parámetro s sería el de la longitud de la cuerda, de tal forma que nos indicaría a qué distancia estamos del punto de origen de la misma.
En esta ocasión las posiciones podrán variar, por tanto en dos sentidos.
Si variamos t, vemos cómo se desplaza un punto de la cuerda en el tiempo.
Si variamos s, nos desplazamos de un punto de la cuerda a sus vecinos.
La superficie espaciotemporal generada al considerar todas las posiciones de la cuerda en el tiempo simultáneamente se denominahoja de cuerda.
Esta nomenclatura, como el principio holográfico, procede de Leonard Susskind.
El módulo cuadrado de las derivadas espacial y temporal de los puntos de la hoja de cuerda se obtienen mediante el producto escalar usual, que denotaremos poniendo los vectores en negrita y obviando sus índices espaciales:
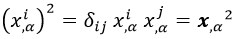
Aquí δij es la métrica euclídea y estamos usando la sumación de Einstein.
El módulo de la variación temporal de un punto de la cuerda es su velocidad v, y por tanto su módulo al cuadrado es la velocidad al cuadrado.
Por otra parte, el módulo de la variación de un punto respecto a la longitud es 1, dado que la derivamos con respecto a sí misma:
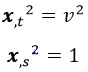
Si consideramos que estamos en el sistema de coordenadas solidario con la cuerda, donde no hay desplazamientos ni rotaciones de la misma, podemos asegurar que los puntos de la misma solo se desplazarán trasversalmente a esta, con lo que la variación temporal y la longitudinal serán perpendiculares y su producto escalar nulo:
Podríamos elegir usar un sistema de coordenadas en el que este producto no tuviese por qué ser nulo, pero también podríamos pegarnos un tiro en el pie y no por eso lo hacemos.
Los momentos de la cuerda tienen dos índices.
Uno que hace referencia a la componente espacial a la que están asociados, y otro que hace referencia a si son momentos temporales o longitudinales:
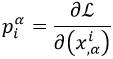
Estos momentos deben estar sometidos a las mismas condiciones que en el caso clásico:
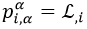
Sabiendo todo esto, para analizar el movimiento de una cuerda son de particular relevancia dos variables: la tensión T y la densidad de masa μ de la misma. La densidad de masa integrada en toda la longitud L de la cuerda tiene que dar la masa M de la misma:
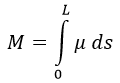
Sabiendo esto, es intuitivo escribir la lagrangiana de la cuerda del siguiente modo:
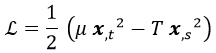
El primer término sería la densidad lineal de energía cinética, y el segundo la densidad lineal de energía potencial.
Este último fue justificado en la entrada sobre ondas, y básicamente es una energía potencial que penaliza que la cuerda se doble.
Los momentos de la cuerda son, dada esta lagrangiana:

Y la restricción que tienen que cumplir lleva a:

Reagrupando y recolocando índices, esto es equivalente a:
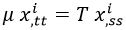
Lo que recuerda a la ecuación diferencial de una onda armónica con velocidad de propagación v:
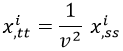
Lo que significa que en una cuerda clásica las oscilaciones se propagan sobre la misma con una velocidad:
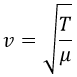
Una vez visto esto, podemos reescribir su ecuación del siguiente modo:
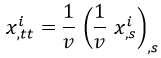
Y aquí a la derecha se puede ver que dos veces consecutivas derivamos las coordenadas espaciales longitudinalmente y las dividimos por la velocidad.
Esto sugiere y pide a gritos un cambio de variable por un parámetro σ tal que se cumpla:
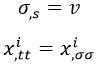
Usando σ como parámetro longitudinal, la velocidad de propagación de la cuerda es 1, con lo que podemos denominarlo el parámetro natural porque simplifica las cosas.
Mediante la regla de la cadena, se obtiene fácilmente que las derivadas de las coordenadas respecto a σ deben cumplir:
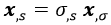
Con lo cual, elevando al cuadrado ambos miembros de la ecuación se puede deducir rápidamente que el módulo cuadrado de x,σ es:
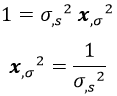
Por otra parte, teniendo en cuenta que lo que aparece derivando era igual a la velocidad de propagación de las ondas sobre la cuerda, llegamos a la conclusión de que el producto de los módulos cuadrados de las derivadas temporal y natural da 1:
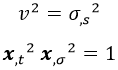
Ojo que esto solo es cierto para cuerdas clásicas y no es extrapolable a lo que sigue.
Cinemática de la partícula relativista:
En relatividad especial, en vez de trabajar con tres coordenadas espaciales y su dependencia con el tiempo, integrábamos el tiempo en la posición dando lugar a una cuadriposición con índice espacio-temporal:
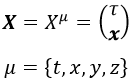
Aquí hemos decidido asignar a la coordenada temporal el tiempo propio τ porque en breves, como antes, elegiremos el sistema de coordenadas solidario con la cuerda y carece de sentido complicarse la vida con tiempos entre diferentes observadores.
Además estamos usando, como siempre, unidades naturales.
Para obtener la norma de un cuadrivector en relatividad especial calculábamos la primera componente al cuadrado y restábamos el módulo cuadrado usual de las componentes espaciales.
Esto venía dado por la métrica ημν de Minkowski, con la ayuda de la cual podíamos definir la métrica g de una superficie relativista de parámetros codificados por α y β:
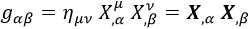
Dada la trayectoria de una partícula parametrizada por un tiempo t, su lagrangiana relativista se definía como el producto entre su masa m y su longitud, y la longitud dependía del determinante de la métrica g:
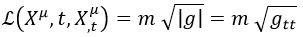
En un caso tan sencillo como una partícula, donde su curva de movimiento viene descrita solo por el tiempo t, su lagrangiana es simplemente el producto entre la masa y la raíz del factor métrico gtt.
Veamos qué sucede con una superficie.
Cinemática de la hoja de cuerda relativista:
Trataremos ahora la hoja de cuerda como una superficie con su métrica g y obtendremos su lagrangiana sin variar la definición de la misma, salvo en un signo que como veremos será necesario:
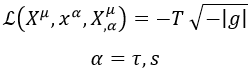
Esta se conoce como la lagrangiana de Nambu-Goto.
¿Por qué en esta ocasión ponemos T en lugar de μ, como sería lógico? La respuesta es que ambas magnitudes son equivalentes en la cuerda relativista, pero lo demostraremos después.
En todo caso lo vamos anticipando porque es la notación usual.
Atendiendo a la definición de la métrica, la de la hoja de cuerda es:
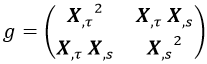
Así que antes de hacer nada necesitamos las derivadas temporal y longitudinal de la cuadriposición, que son:
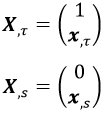
Y los productos escalares relativistas que necesitamos dan:
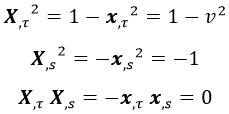
Con lo que la métrica de la hoja de cuerda es:
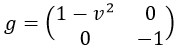
Y por tanto la lagrangiana toma la siguiente forma:
Queda con esto justificado el signo negativo que pusimos dentro de la raíz, dado que de otro modo nos habría quedado compleja porque la velocidad trasversal siempre es menor o igual que 1.
No obstante, hay que trabajar con la expresión del medio porque es la única expresada en los parámetros correctos.
Los cuadrimomentos asociados a la hoja de cuerda son:
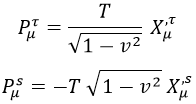
A partir de la segunda expresión nótese que si, por ejemplo, quisiéramos que en un punto cualquiera de la cuerda su cuadrimomento longitudinal fuese nulo (no transportase cuadrimomento hacia ningún lado), esto implicaría que en ese punto la cuerda se tendría que mover a la velocidad de la luz.
Por otra parte, ya sabemos que la primera componente del cuadrimomento temporal es la energía relativista, o en este caso la densidad lineal de energía, con lo que podemos hacer la siguiente identificación:
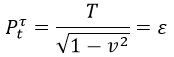
Y comparando con la fórmula de la energía relativista especial en función de la masa llegamos a la conclusión de que efectivamente la tensión y la densidad lineal de masa son equivalentes, como habíamos anunciado:
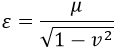
Ahora bien, teniendo los cuadrimomentos llegamos a la siguiente condición:
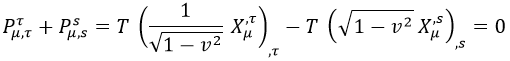
Para apañarla un poco, podemos pensar en qué pasa si fijamos quedarnos con la primera componente en cada caso, y concretamente lo que sucede es que llegamos a la conclusión de que la energía de la hoja de cuerda se conserva:
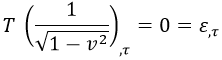
Con lo que teniendo en cuenta que este factor puede salir como una constante de las derivadas temporales, reagrupando y reubicando índices tenemos de nuevo una ecuación de onda:
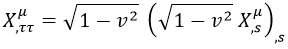
Que en esta ocasión pide a gritos la siguiente parametrización natural:
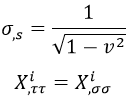
Despejando de la ecuación de arriba:
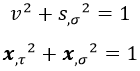
Y comparando con las normas de los cuadrimomentos esto es:
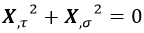
No hay que sorprenderse de que dos normas al cuadrado sumen 0 en relatividad especial, y menos aún si se tiene en cuenta que la derivada temporal es un cuadrivector tipo tiempo de norma cuadrada positiva y la derivada natural es un cuadrivector tipo espacio de norma cuadrada negativa.
Además de esta relación, ambos cuadrivectores siguen siendo ortogonales en tanto que la derivada natural es proporcional a la derivada longitudinal:
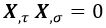
Y gracias a estas dos últimas condiciones combinadas podemos decir que la siguiente ecuación es cierta:
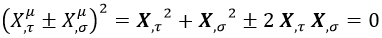
Teniendo en cuenta todo esto con σ, la lagrangiana y los cuadrimomentos quedan del siguiente modo mucho más sencillos:
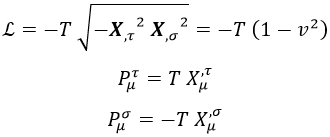
En la siguiente entrada sobre esto veremos cómo permiten todas estas condiciones oscilar a una hoja de cuerda.
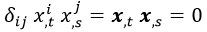
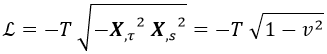
No hay comentarios:
Publicar un comentario