El controvertido efecto Casimir

Hendrik Casimir

Vamos a tratar de explicar en varias entradas qué es el efecto Casimir. 

Este es un efecto muy interesante pero tiene varios problemas.

En estas entrada queremos hacer lo siguiente:

– Explicar a un nivel muy básico el mencionado efecto.  Para ello introduciremos ciertas aproximaciones pero intentando preservar en todo momento la esencia del fenómeno.

–  Indicar cuáles son las aproximaciones introducidas y explicar cómo se podría extender esta discusión a casos más “formales”.

–  Puntualizar lo que no implica el efecto Casimir.  Este efecto ha dado mucho que hablar y ha suscitado algunos malentendidos.

¿En qué consiste el efecto Casimir?

Si disponemos en el vacío dos espejos perfectos separados por una distancia pequeña estos se atraen entre si.

Explicaremos esto:

–  Supongamos que tenemos dos espejos perfectos =  Reflejan todas las frecuencias de las ondas electromagnéticas.

–  Suponemos que son planos.

–  Disponemos de una región donde tenemos vacío, es decir, no hay nada de nada.

– En dicha región ponemos los dos espejos separados por una distancia pequeña (del orden del micrómentro o del nanómetro).

Y el resultado es que estos espejos se atraen.  

Lo cual es contraintuitivo porque estos planos no están cargados, no hay cargas en el medio así que en principio no hay razón alguna para que aparezca una fuerza de atracción entre ambos espejos.

Cuestiones ondulatorias

Ya hemos hablado algunas veces de las propiedades de las ondas. 

La longitud de onda, periodo y frecuencia en ondas:

Longitud de onda  –  Distancia entre dos puntos de la onda que se encuentran en el mismo estado de vibración.  Por ejemplo dos crestas de la onda o dos valles, por decir algo, nos valdrían cualquier par de puntos consecutivos en el mismo estado oscilatorio.

Periodo 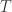 –  Nos dice cuanto tiempo ha de pasar para que un punto de la onda vuelva a una determinada posición.  Es decir, nos fijamos en un punto que está en un valle y contamos el tiempo que pasa hasta que dicho punto vuelve a estar en el valle (podemos tomar cualquier otra posición como referencia). 

 Es decir, el periodo es el tiempo que tarda en completarse una oscilación:

Frecuencia  – La frecuencia nos dice cuantas oscilaciones se producen por unidad de tiempo.  Por lo tanto la frecuencia es simplemente el inverso  del periodo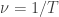 

Una onda tiene una velocidad de propagación, la ondas electromagnéticas se propagan a la velocidad de la luz cuando se mueven en el vacío.  Dado que la velocidad es básicamente espacio recorrido por unidad de tiempo, en una onda tenemos una forma excelente de calcular su velocidad dividiendo su longitud de onda entre su periodo:

Pero como existe una relación entre el periodo (medido en segundos) y la frecuencia (medida en (1/segundos) = Herzios (Hz)) podemos escribir:

Para las ondas electromagnéticas tendremos:

Ahora pensemos que ocurre cuando una onda por ejemplo en una cuerda con los extremos fijados.

Si la longitud de la cuerdas es L las longitudes de onda que admite el sistema tienen que cumplir:

Es decir, que las longitudes de onda admitidas en la cuerda con extremos fijos tienen que cumplir que si multiplicamos la mitad de dicha longitud de onda por un número natural (1,2,3,4,…) nos tiene que salir la longitud de la cuerda.

El vació cuántico: La visión perturbativa

Ahora nos adentramos en la cuántica.  En esta teoría el vacío revela que tiene “estructura”, es decir, que influye en el comportamiento de determinados fenómenos en los sistemas cuánticos (echar un vistazo al Efecto Lamb del que ya hablaremos en su momento).

Nota de Advertencia: 

La forma en la que en divulgación se trata del tema procede de lo que se conoce como tratamiento perturbativo de la teoría cuántica de campos.  Hemos de dejar claro que lo que vamos a exponer ahora es simplemente una forma de describir el fenómeno pero en absoluto es la “imagen real”, de hecho no sabemos cómo es esa imagen, lo único que sabemos es que el fenómeno se produce pero no el cómo “de verdad”. Lo que vamos a explicar es una descripción en palabras de una de las formas en que que podemos calcular este efecto, pero tiene que quedar claro que es una descripción asociada a un procedimiento matemático.  

El ingrediente:  La indeterminación

En cuántica tenemos el hecho de que hay pares de magnitudes que no están definidas simultáneamente.  Es decir, que si conocemos una de ellas la otra está totalmente indeterminada y no tenemos ni idea de su valor.  Esto es lo que nos dice el principio de Indeterminación de Heisenberg. El ejemplo típico es la posición y la velocidad de una partícula.  

Si conocemos su posición no conocemos su velocidad y viceversa.

Otro par de magnitudes que verifican el principio de indeterminación de Heisenberg son la energía de un sistema y el tiempo que tardamos en medirla.

Es decir, que si podemos medir instantáneamente la energía del sistema entonces el sistema no nos daría respuesta alguna.  Y si medimos la energía del sistema no sabemos en qué instante la hemos determinado.

Esto es muy importante por lo siguiente:

1.-  Si definimos el vacío cuántico como aquel sistema que no contiene nada presuponemos que su energía es nula (esto siempre podemos suponerlo).

2.-  Pero resulta que si la energía del sistema siempre es nula entonces conoceríamos en todo instante la misma, lo cual violaría el principio de indeterminación.

3.-  Como conclusión hemos de aceptar que el vacío es un sistema que está teniendo fluctuaciones de energía de forma que su promedio es nulo. Es decir, el vacío subirá espontáneamente su energía siempre y cuando dicha subida se reabsorba tan rápido que no de tiempo a medirla.

4.-  Cuanto mayor es la fluctuación en la energía menor será el tiempo que puede sobrevivir.

¿Pero en qué forma se presentan estas fluctuaciones?

Pues en la forma de aparición de partículas, fotones, electrones, positrones, etc. Las flutuaciones tienen que crear siempre pares de partícula – antipartícula de forma que se puedan aniquilar para devolver la energía prestada por el vacío al mismo y el promedio quede nulo.

La imagen típica de esto es:

Las partículas y antipartículas (rojo y azul) aparecen y se vuelven a aniquilar. Estas partículas aparecen porque “roban” energía del vacío y luego se aniquilan para devolver esta energía de forma que el promedio no varíe.  Cuanto mayor es la masa del par de partículas producido más rápida será su desaparición en el vacío.

Evidentemente lo más fácil de producir son fotones ya que son partículas sin masa ni carga.  Y aquí está la clave.

¿Qué tiene todo esto que ver con el efecto Casimir?

Intentaremos ser muy explícitos siguiendo la imagen que estamos proponiendo (Hay que recordar que esto sólo es una forma de contarlo):

1.-  Tenemos el vacío cuántico, que está continuamente fluctuando y por tanto creando y destruyéndose partículas en su interior.

2.-  Mayoritariamente se crean y destruyen fotones.  Y hemos de recordar que los fotones se puede considerar ondas (dualidad onda-corpusculo), de hecho su energía corresponde a su frecuencia 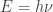 que también se puede reescribir en términos de su longitud de onda:

donde hemos empleado que 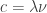.  En el vacío por lo tanto se pueden crear fotones de cualquier energía (siempre que desaparezcan antes de poder ser medido) y eso implica de cualquier longitud de onda.

3.-  Ahora introducimos dos espejos planos perfectos.  Pero los espejos reflejan, ese es su trabajo, pero reflejar significa que el fotón no puede traspasar el espejo.  Así pues introducir los dos espejos equivale en el caso de las ondas que hemos hablado antes a tener una cuerda con los dos extremos fijos.  En ese caso la cuerda no puede moverse a partir de los extremos fijos.  

En el caso de los fotones esto es lo que ocurren cuando llegan al espejo.

4.-  Por lo tanto estamos modificando la estructura del vacío ya que entre los espejos no podemos tener cualquier fotón de cualquier energía.  

Si la separación entre los espejos es d, las longitudes de onda de los fotones tienen que ser consistentes con eso, .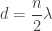

Una imagen de esto es:

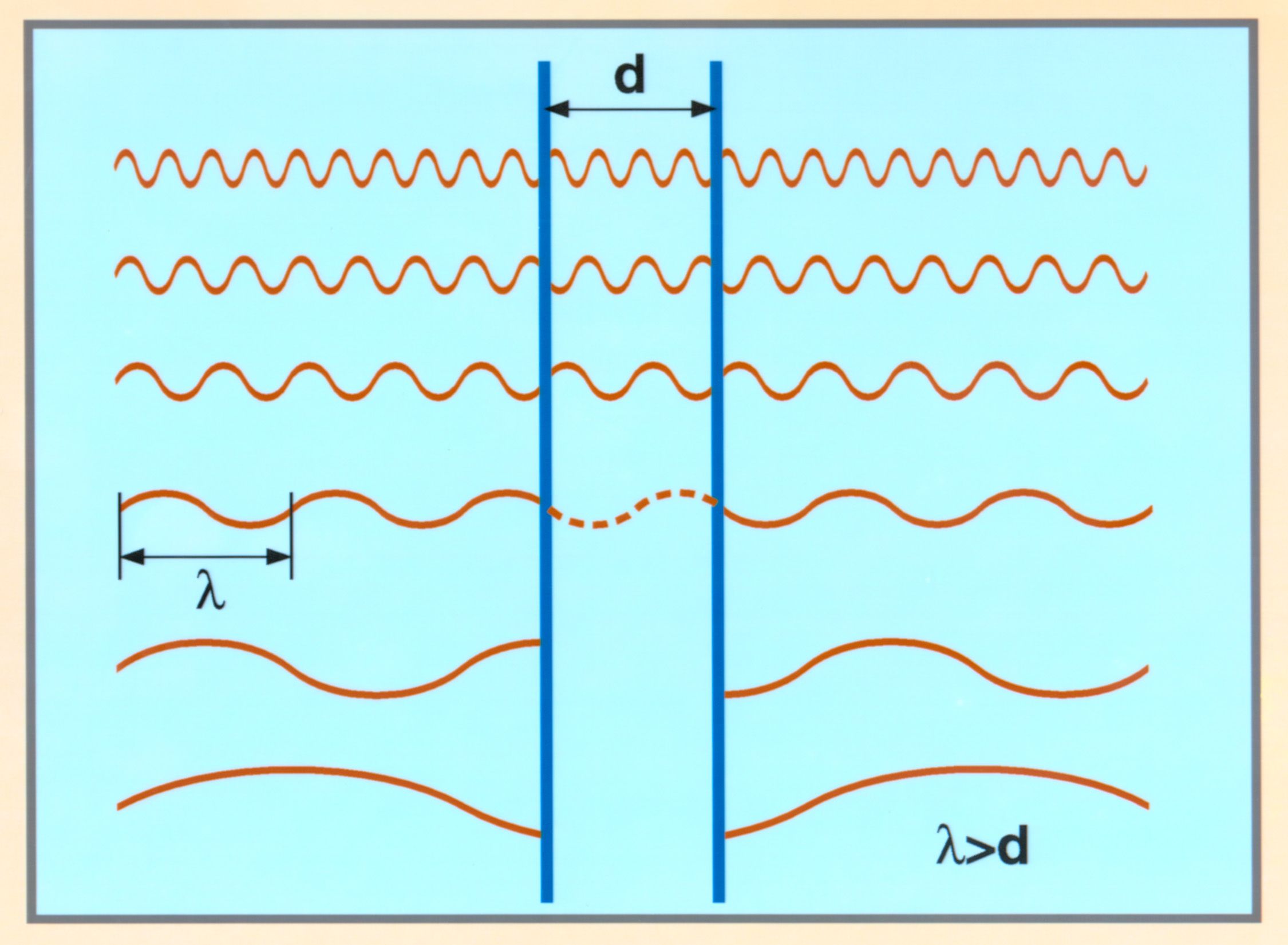
Esto implica que entre los espejos no podemos tener todos los fotones que sí que pueden crearse fuera de los mismos.  Pero la luz, los fotones tienen energía, y pueden empujar a los espejos. Pensemos que una reflexión se puede considerar como una colisión del fotón con el espejo de forma que este rebota.

Como en el interior de los espejos hay “menos fotones” que fuera, los de la zona exterior del espejo producen una presión que hace que los espejos se junten dando lugar a un efecto de atracción entre los mismos.

La presión producida por el exterior (fuerza por unidad de área del espejo) es:

donde h es la constante de Planck, c es la velocidad de la luz y d es la distancia entre los espejos.  Notemos que la distancia va elevada a cuatro y entra en la fórmula dividiendo.  

Eso quiere decir que si aumentamos la distancia de 1 a 10, pasamos a dividir por una cantidad 10000 mayor, reduciendose el efecto. 

 Es por eso que los espejos tienen que estar muy juntos (además de que la constante de Planck es muy pequeña). 

 Es por eso que este efecto sólo se da en rangos de separación de micro o nanómetros.

¿Qué queda por contar?

Quedan muchas cosas pero más técnicas como veremos. Queda hablar de que la energía dentro de los espejos es infinita según nuestras teorías y que fuera también lo es.  Queda por comentar la relación entre este efecto y la constante cosmológica.  Queda por explicar por qué no podemos usar este fenómeno para construir máquinas grandes que extraigan energía del vacío (ver Hablando de Ciencia: La máquina que produce más energía de la que consume (o eso dice su creador) para una introducción al tema).

 Queda hablar de qué pasa si empleamos espejos de otras formas, por ejemplo esferas. Quedan muchas cosas por contar. 

Iremos poco a poco.

Nos seguimos leyendo…