El símbolo de Levi-Civita ya ha aparecido en este blog en varias ocasiones.
Sin embargo, nunca he dedicado una entrada a su representación en varias dimensiones como la representación de puntos de hipercubos.
En esta entrada, planteada a petición, veremos cómo representarlo en cuatro dimensiones por su interés intrínseco para los fans de la geometría.
Nociones sobre el Levi-Civita:
El símbolo alternante de Levi-Civita es un pseudo-tensor antisimétrico que solo tiene sentido definir con un número de componentes iguales al número de dimensiones del espacio en el que se encuentre.
Esto implicaba que su número de componentes independientes siempre es 1 y que su número de componentes no nulas es el factorial deD, siendo D el número de dimensiones del espacio.
- En 1 dimensión es un tensor de rango 1 como 1 componente no nula.
- En 2 dimensiones es un tensor de rango 2 con 4 componentes, de las cuales 2 son no nulas.
- En 3 dimensiones es un tensor de rango 3 con 27 componentes, de las cuales 6 son no nulas.
- En 4 dimensiones es un tensor de rango 4 con 256 componentes, de las cuales 24 son no nulas.
- En n dimensiones es un tensor de rango n con n^n componentes, de las cuales n! son no nulas.
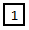
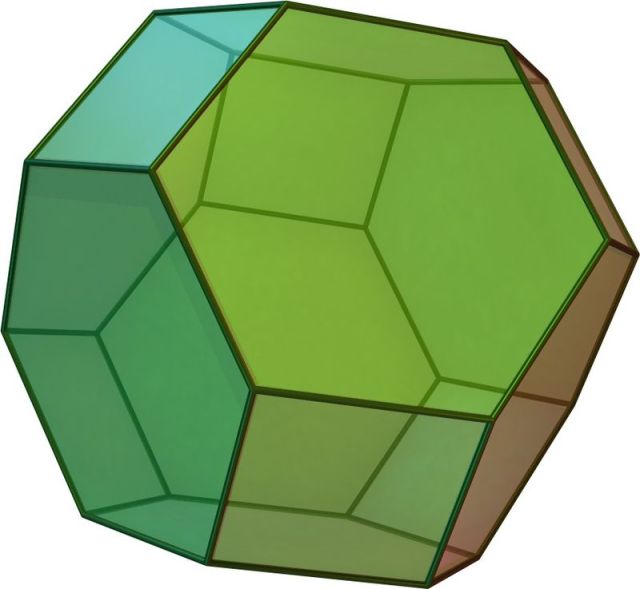
El Levi-Civita en dimensión 1:
Este no tiene mucho misterio, simplemente tiene una componente que vale 1.
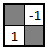
El Levi-Civita en dimensión 2:
Aquí entramos en el plano y debemos representarlo como una matriz 2×2, en la cual los elementos de la diagonal son nulos y los otros dos son no nulos, valiendo 1y el otro -1. La unión del centro de ambas celdas da lugar a un segmento cuya longitud vale, teorema de Pitágoras mediante, raíz de 2.
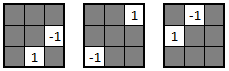
El Levi-Civita en dimensión 3:
Aquí entramos en el espacio y debemos representarlo como un cubo 3x3x3.
Dicho cubo podemos representarlo sencillamente indicando qué valores toman sus celdas en los pisos primero, segundo y tercero. En la imagen, está hecho de izquierda a derecha.
Se puede observar que cada planta contiene, sin lugar a dudas, un Levi-Civita de dimensión 2: en todas la diagonal está anulada y contienen solo dos elementos no nulos que valen 1 y -1. Por otra parte, en la primera planta se anulan la primera fila y la primera columna, en la segunda las segundas y en la tercera las terceras.
Si se montase todo el cubo con las tres plantas y se uniesen las celdas no nulas se vería un hexágono regular de lado raíz de 2, de nuevo Pitágoras mediante.
El Levi-Civita en dimensión 4:
Aquí entramos en el hiperespacio y la figura a representar sería un hipercubo 4x4x4x4, más conocido como un teseracto. No obstante, es bien sabido que no podemos dibujar figuras de 4dimensiones siendo unas humildes criaturas que no vemos más allá de 3, y por tanto representar esto tiene su complicación.
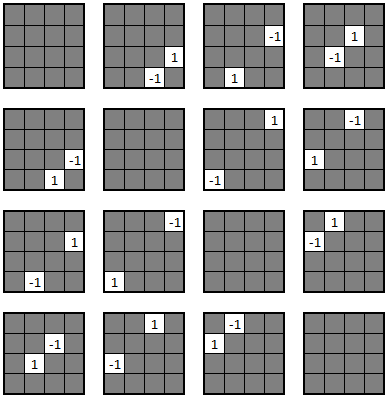
En analogía con la representación de antes, podemos ampliar las celdas añadiendo 4 filas nuevas hacia abajo que representarían la nueva dimensión.
En cada fila, o valor de la cuarta dimensión, tenemos obviamente Levi-Civitas de dimensión 3, que a su vez en cada cuadrado contienen Levi-Civitas de dimensión 2. Las diagonales se anulan tanto en los cuadrados pequeños como en los grandes.

Ahora bien, ¿cómo se ve esto en 4 dimensiones? ¿Qué figura forma?
Por suerte la respuesta a esta pregunta es fácil de obtener y de explicar. Pensemos en un cubo 3x3x3, donde cada vértice representa el centro de una de nuestras celdas.
Consideremos que la cuarta dimensión es el tiempo.
La primera fila representaría el instante 1, la segunda el 2…
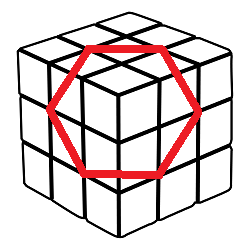
En el instante inicial tendríamos que la planta baja del cubo estaría vacía y entre las tres de arriba aparecería un hexágono.
Esto es obvio dado que contiene un Levi-Civita de dimensión 3.
La distancia entre todos los puntos de dicho hexágono es, ¡gran sorpresa!, raíz de 2 de nuevo.
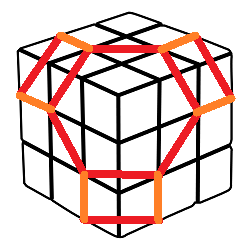
Pasemos al segundo instante. Aparecerán otros seis puntos nuevos. Pero en vez de unirlos entre ellos formando otro hexágono (cosa posible, si bien sería irregular) lo que haremos es unirlos a pares y con los puntos del hexágono original que tengan más próximos tal y como se indica en la figura.
Las uniones entre puntos nuevos las haremos de color rojo y las uniones entre puntos nuevos y viejos de color naranja. Si nos fijamos, todas las líneas rojas medirán raíz de 2 aplicando el teorema de Pitágoras habitual, mientras que las naranjas serán aparentemente más cortas.
No obstante, si tenemos en cuenta que las líneas naranjas avanzan también en la cuarta dimensión un pasito miden lo mismo. Así pues, tenemos un hexágono regular y tres cuadrados regulares.

Al pasar al tercer instante simplemente hacemos lo mismo. Añadimos otros seis puntos y los juntamos dos a dos y con sus vecinos siguiendo las mismas reglas que antes.
Si todo se hace bien, aparecen otros tres hexágonos regulares, tal y como se ve en la figura.
El cuarto instante tiene puntos que no aparecen en el lado visible del cubo, pero que son simétricos a los de nuestro primer hexágono por el lado oculto.
De hecho, al completar los cuatro instantes tenemos la imagen del tercer instante por un lado y la misma invertida por el otro, encajando todo perfectamente y dando lugar a un octaedro truncado de 8 hexágonos regulares y 4 cuadrados regulares, todos ellos de lado raíz de 2.
¡Y ya tenemos nuestra representación del Levi-Civita de dimensión 4!
No hay comentarios:
Publicar un comentario