Hay infinitos números primos. Demostración de Euclides

Veremos la demostración de Euclides de la infinidad de números primos, pero primero a aclarar algunas cosas que nos facilitarán entender la demostración:

• Un número primo es aquel que, siendo diferente de , sus dos divisores son el  y él mismo. Los demás números se denominan compuestos, pues pueden ser expresados como el producto de primos.
• 
  
•  Por ejemplo, el número , que no es primo sino compuesto, puede expresarse multiplicando , que sí son primos.

• Los divisores de un número  son aquellos  tal que el resultado de la división  es un número entero. Y tenemos que  (el valor absoluto, o la magnitud, de  es menor o igual que la de ).
• 
  
•  Por ejemplo, los divisores de son  y  y sus factores primos  y .

• El residuo de una división es un número  tal que si tenemos dos números  y que estamos dividiendo, se cumple que  siendo  la parte entera del cociente.
• 
  
•  Esto se conoce como el algoritmo de la división. Por ejemplo, si queremos dividir  entre  tenemos que (siendo  y )  ya que el  “cabe” dos veces en el  y para llegar a ser  le faltan , que es nuestro residuo.

Hay varias vías para demostrar que el conjunto de los números primos es infinito. Esta demostración es atribuida a Euclides, por allí del 300 a.C.

Teorema: Hay una infinidad de números primos.

Demostración: Lo haremos por reducción al absurdo, es decir, supondremos cierto lo contrario y llegaremos a una contradicción, que significará que lo que negamos realmente es verdadero.

 La reducción al absurdo es una herramienta muy usada en matemáticas y muy efectiva.

Supongamos que  son todos los primos que existen, son elementos, un número finito (estamos negando el teorema para luego llegar a una contradicción: reductio ad absurdum).

Sea  un número. 

Vemos que, por construcción, 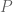 es un  número mayor que cualquier primo, ya que es la multiplicación de todos estos mas . 

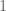Y al dividir 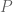 entre cualquiera de los primos, el residuo es  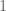(si no se entiende bien este paso, véase el punto 3 de los anteriores, note que el 8 está escrito como el producto de dos primos,  mas un residuo, , lo mismo pasa aquí, en este caso el residuo es ).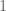 

Esto significa que 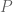 es o un número primo u otro número (no conocemos su identidad), pero si es primo, tiene que ser mayor a cualquier otro primo (puesto que es la multiplicación de todos ellos mas 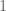), entonces los que supusimos que eran los únicos primos,  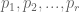no son todos los números primos; y si  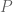no es primo, eso quiere decir que existe un primo que divide a 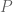, y no es ninguno de los anteriores (puesto que los demás primos dejan  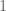como residuo, así que tiene que ser otro primo que no deje residuo al efectuar la división).

Entonces, para cualquiera de los dos casos llegamos a que existe otro primo que no está en nuestra lista inicial, y por tanto la suposición de un número finito de números primos es falsa. Hemos llegado a una contradicción partiendo de la negación del teorema.

Por tanto, hay una infinidad de números primos.

Personalmente, esta demostración me parece muy elegante y sencilla.

 Espero haber sido claro. 

Einstein en una ocasión dijo: “No entiendes realmente algo a menos que seas capaz de explicarselo a tu abuela”, aunque en este caso no tenga la necesidad de explicárselo a mi abuela.