Papá ¿qué son las simetrías C, P y T?

Bueno, esto es continuación de la entrada Papá ¿por qué hay materia? .

 Así que vamos a dedicarnos a explicar un poco las transformaciones y simetrías que serán útiles para entender eso de la asimetría materia/antimateria.

La transformación P = Paridad: simplemente hace esto,

Es decir, toma un vector y lo convierte en su opuesto.

Visualmente esto es lo siguiente: Toma un vector, refléjalo en un espejo y rotaló.

Pero atención, no todo es tan fácil como parece:

Si tenemos el momento lineal  y le aplicamos una transformación de paridad, obtenemos .

Ahora bien, ¿qué pasa con el momento angular? (que es el “vector” que nos indica cuanto está rotando un sistema)

El momento angular se define con un producto vectorial: .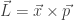

 Si aplicamos la paridad pues cambian tanto el vector posición como el vector momento, con lo cual el momento angular permanece igual.

Esto es genial, porque ahora tenemos un método de clasificación de vectores:

Vectores polares: Cambian de signo bajo paridad.

Vectores axiales: No cambian de signo bajo paridad.

Pero claro, los vectores también se puede multiplicar escalarmente: 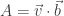donde A es un número (un escalar).

 Entonces también tendremos una clasificación de los escalares provinientes de productos escalares de vectores en términos de su comportamiento bajo paridad:

Escalares: Producto de dos vectores polares o dos vectores axiales. 

No cambian de signo bajo paridad

Pseudo escalares: Producto de un vector polar con uno axial. 

Sí cambian de signo bajo paridad.

La transformación T = Inversión temporal: cambia el sentido de las velocidades, que se puede traducir como cambiar t por -t, dejando 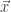 sin tocar.

Es claro ver que el momento lineal cambia de signo (ya que depende de la velocidad). Y el momento angular también cambia de signo (ya que depende del momento lineal).

La transformación C = Conjugación de carga: Convierte a una partícula en su antipartícula. Es decir, conserva masas, momentos, pero todas las cargas aditivas (que se pueden sumar) son opuestas. 

La más representativa de estas cargas es la carga eléctrica pero hay otras que por el momento nos dan un poco igual.

Ejemplos:

Es fácil ver cómo las leyes de la mecánica de Newton son invariantes bajo C, P y T. Entonces se dice que dichas leyes son simétricas respecto a las transformaciones C, P y T.

Si aplico la transformación de paridad a estas cantidades:

Por lo tanto la fórmula queda igual F=ma.

La cosa es idéntica con T y con C (aquí C pinta poco).

Lo mismo se puede probar para las ecuaciones de Maxwell, quedan exactamente igual bajo transformaciones de C, P y T.

Por supuesto también podríamos estudiar diferentes combinaciones de estas simetrías: CP, CT, PT, CPT (esto quiere decir, aplica primero T, al resultado le aplicas P y al resultado le aplicas C). Sin embargo, las más interesantes son CP, y CPT.

¿Por qué son estas las interesantes?

CP va a controlar la simetría materia-antimateria. 

Así que le daremos una entrada propia.

Y CPT es la reina del baile. Así que intentemos entenderla un poco.

Transformación y Simetría CPT:

Esta transformación es un elemento clave en una teoría cuántica de campos (QFT en lo que sigue). 

Para no complicarnos mucho diremos (ya tendremos oportunidad de extendernos en qué es una QFT):

Teoría cuántica de campos (QFT)= mecánica cuántica + relatividad especial

Por tanto, hay un principio fundamental que una QFT tiene que satisfacer, y es que si medimos un campo cuántico (sea eso lo que sea por el momento), en puntos tan separados que no sea posible conectarlos por un rayo de luz (es decir que para saber lo que pasa en el otro punto tengamos que usar cosas superlumínicas) estas medidas no se afectan la una a la otra. 

Esto es lo que se llama un principio de localidad. 

Y resulta que este principio condensa toda la esencia de la QFT.

Pero resulta que esto se puede traducir de otro modo:

Una QFT siempre tiene que ser invariante bajo CPT. Y esto es un teorema demostrable dentro del formalismo, y el único ingrediente que necesitamos para demostrarlo es: relatividad especial (invariancia Lorentz).

Vamos que CPT no es más que asegurar que se cumplen las leyes de la relatividad en una teoría cuántica de campos, que por definición es lo que queremos al construir tales teorías. (Técnicamente se dice que CPT implica la invariancia Lorentz de la teoría en cuestión, que implica la existencia de un único estado de vacío y que se respeta el principio de localidad).

Lo interesante de todo esto son sus consecuencias:

1. Una partícula y su compañera antipartícula (electrón positrón por ejemplo) tiene la misma masa y la misma vida media (en caso de ser partículas inestables).

2. Los momento magnéticos dipolares son iguales en magnitud y opuestos en sentido. (Esto es lo que permite distinguir a un neutrón de un antineutrón que en principio no serían distinguibles por ser partículas neutras).