Consideremos un polinomio  con coeficientes
con coeficientes 
El módulo máximo de  en la circunferencia unidad viene dado por
en la circunferencia unidad viene dado por
Una cota inferior para  es la norma hilbertiana
es la norma hilbertiana
Se sigue de la identidad de Parseval que  y por lo tanto
y por lo tanto
Se plantea el problema de hallar polinomios  de grado
de grado  tales que
tales que 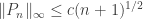 donde
donde  es una constante.
es una constante.
Una solución muy ingeniosa viene dada por medio de un procedimiento inductivo descubierto independientemente por W. Rudin y H.S. Shapiro. Sean  y sean
y sean
Está claro que  son polinomios de grado
son polinomios de grado 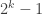 con coeficientes
con coeficientes 
Además se tiene
de donde se deduce que  de modo que si
de modo que si  o
o  entonces
entonces 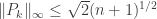 donde
donde 

No hay comentarios:
Publicar un comentario